代码随想录Day.23 | 669. 修剪二叉搜索树、108. 将有序数组转换为二叉搜索树、538. 把二叉搜索树转换为累加树

669. 修剪二叉搜索树

1. LeetCode链接

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

2. 题目描述

 

 

3. 解法

递归法：

此题抽象点来看，就是将树两侧不在[low, high]区间内的分支修剪掉，保留中间的一部分。

root节点的值有三种情况：

        1. root->val < low

        2. root->val > high

        3. root->val 恰好再[low, high]区间内

        针对情况1，说明要保留的中间部分在root->right上；针对情况2，说明要保留的中间部分在root->left上；针对情况3，说明要保留的部分树的根节点，就是rootbenshen。

        而通过递归，最终都会归为解决情况3。

        针对情况3，要在root树中，假如某个节点恰好小于low，则要删除该节点及其左子树，即令其右子树替代他；假如某个节点恰好大于high，则要删除该节点及其右子树，即令其左子树替代他。

        如何找这两个恰好小于low，恰好大于high的节点？通过双指针的中序遍历！

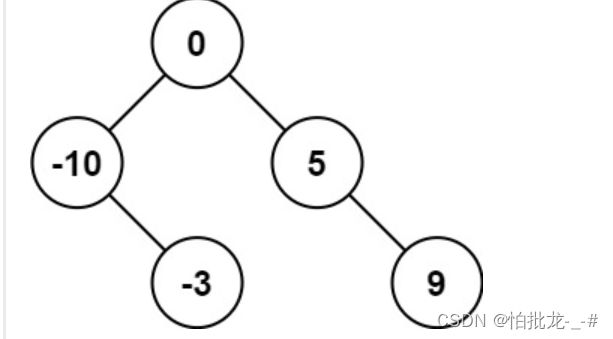
1. 为什么找恰好小于low的节点，而不是恰好大于low的节点？找恰好大于low的节点时，即用正常左中右的中序遍历，pre指针指向前一个，判断root是要找的节点条件是(pre != NULL && pre->val < low && root->val >= low)此时，root根本不是要删除的，而删除pre比较困难，而且可能存在root是pre右子树中的值这种情况，处理起来更麻烦。如下图pre是0，root是1的情况。

所以只能找恰好小于low的节点。这就用到右中左——倒序中序遍历。此时保证满足条件(prel != NULL && prel->val >= val && root->val < val)即可找到。删除root及其左子树就是直接返回其右子树。

2. 找恰好大于high的逻辑同上。正常左中右中序遍历即可。

class Solution {
public:
    TreeNode* prel = NULL;
    TreeNode* prer = NULL;
    TreeNode* highOrder(TreeNode* root, int val) {
        if (root == NULL) return NULL;
        root->left = highOrder(root->left, val);
        if (prer != NULL && prer->val <= val && root->val > val) return root->left;
        prer = root;
        root->right = highOrder(root->right, val);
        return root;
    }
    TreeNode* lowOrder(TreeNode* root, int val) {
        if (root == NULL) return NULL;
        root->right = lowOrder(root->right, val);
        if (prel != NULL && prel->val >= val && root->val < val) return root->right;
        prel = root;
        root->left = lowOrder(root->left, val);
        return root;
    }
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == NULL) return NULL;
        if (root->val < low) return trimBST(root->right, low, high);
        else if (root->val > high) return trimBST(root->left, low, high);
        root = lowOrder(root, low);
        root = highOrder(root, high);
        return root;
    }
};

还有更简单的递归逻辑：
        这个逻辑考虑到，三种情况通过递归，都会归为情况1或者情况2。正常的“重连”遍历递归方法就行。

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == nullptr) return nullptr;
        if (root->val < low) return trimBST(root->right, low, high);
        if (root->val > high) return trimBST(root->left, low, high);
        root->left = trimBST(root->left, low, high);
        root->right = trimBST(root->right, low, high);
        return root;
    }
};

108. 将有序数组转换为二叉搜素树

1. LeetCode链接

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

2. 题目描述

3. 解法

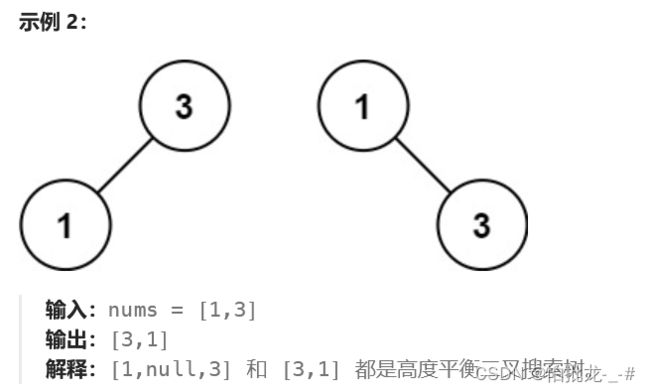
因为要高度平衡，每次取中间树当作节点即可。

注意，mid = (high + low) / 2 而不是mid = (high - low) / 2。

class Solution {
public:
    TreeNode* buildTree(vector& nums, int low, int high) {
        if (low > high) return NULL;
        int mid = (high + low) / 2;
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = buildTree(nums, low, mid - 1);
        root->right = buildTree(nums, mid + 1, high);
        return root;
    }
    TreeNode* sortedArrayToBST(vector& nums) {
        return buildTree(nums, 0, nums.size() - 1);
    }
};

538. 把二叉搜索树转换为累加树

1. LeetCode链接

. - 力扣（LeetCode）

2. 题目描述

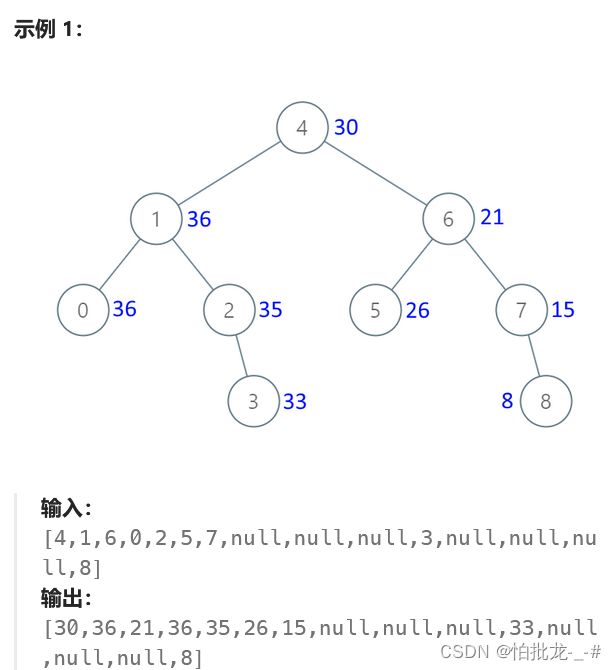
3. 解法

右中左中序遍历双指针递归法

class Solution {
public:
    TreeNode* pre = NULL;
    TreeNode* convertBST(TreeNode* root) {
        if (root == NULL) return NULL;
        root->right = convertBST(root->right);
        if (pre != NULL) root->val += pre->val;
        pre = root;
        root->left = convertBST(root->left);
        return root;
    }
};