聚类算法DBSCAN笔记

内容简介

DBSCAN的实例流程笔记。第一部分记录了算法的相关概念，第二部分用简单的例子说明如何用python实现DBSCAN算法。

1. DBSCAN基本概念

DBSCAN(Density-Based Spatial Clustering of Applications with Noise)将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在噪声的空间数据库中发现任意形状的聚类。

1）DBSCAN中的定义

• Ε邻域：给定对象半径为Ε内的区域称为该对象的Ε邻域；
• epsilon：在一个点周围邻近区域的半径
• MinPts（minPoints ）：密度阈值，即Ε邻域内点的最小数量。
• 核心对象：如果给定对象Ε邻域内的样本点数大于等于MinPts，则称该对象为核心对象；

4种点与点的关系：

• 直接密度可达（密度直达）：对于样本集合D，如果样本点q在p的Ε邻域内，并且p为核心对象，那么对象q从对象p直接密度可达。

• 密度可达：对于样本集合D，给定一串样本点p1,p2….pn，p= p1,q= pn,假如对象pi从pi-1直接密度可达，那么对象q从对象p密度可达。密度可达是直接密度可达的传递闭包，并且这种关系是非对称的

• 密度相连：存在样本集合D中的一点o，如果对象o到对象p和对象q都是密度可达的，那么p和q密度相联。密度相连是对称关系。DBSCAN目的是找到密度相连对象的最大集合
  
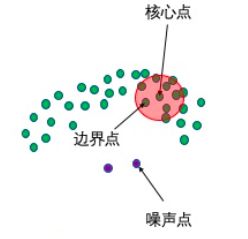
  点的类别

• 核心点：E邻域至少包含最小数目MinPts的点。

• 边界点：在边界上，在核心点的邻域内，但不是核心点。

• 噪音点：落单的点，不是核心也不是边界，和其他点搭不上关系。
  

2）例子

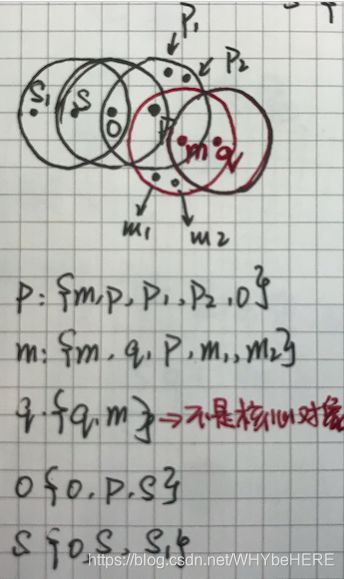
假设半径Ε=3，MinPts=3，点p的E邻域中有点{m,p,p1,p2,o}, 点m的E邻域中有点{m,q,p,m1,m2},点q的E邻域中有点{q,m},点o的E邻域中有点{o,p,s},点s的E邻域中有点{o,s,s1}.
那么核心对象有p,m,o,s(q不是核心对象，因为它对应的E邻域中点数量等于2，小于MinPts=3)；
点m从点p直接密度可达，因为m在p的E邻域内，并且p为核心对象；
点q从点p密度可达，因为点q从点m直接密度可达，并且点m从点p直接密度可达（p= =>m= =>q, 两个点都在m的E邻域内)；
点q到点s密度相连，因为点q从点p密度可达，并且s从点p密度可达。(s<= =o< ==p == >m= =>q)

下面手画个草稿渣图(忽略颜色）：

3) 步骤

DBScan需要二个参数： 扫描半径 (eps)和最小包含点数(minPts)。

1. 任选一个未被访问(unvisited)的点开始，找出与其距离在eps之内(包括eps)的所有附近点。
2. 如果 附近点的数量 ≥ minPts，则当前点与其附近点形成一个簇，并且出发点被标记为已访问(visited)。 然后递归，以相同的方法处理该簇内所有未被标记为已访问(visited)的点，从而对簇进行扩展。
3. 如果 附近点的数量 < minPts，则该点暂时被标记作为噪声点。
4. 如果簇充分地被扩展，即簇内的所有点被标记为已访问，然后用同样的算法去处理未被访问的点

可视化链接Visualizing DBSCAN Clustering图解整个迭代流程步骤。

4）优缺点

**优势：**无需制定簇的个数k，可发现任意形状的簇；擅长找到离群点/异常点；只需要两个参epsilon和MinPt
缺点：（（处理高维数组有困难（可用降维方法）；参数对结果影响大，调参复杂；效率较慢（可用数据削减策略）；不适合密度不均匀的样本集。

2. 代码实例

首先，让我们将训练集聚类为50个集群， 然后对于每个聚类，让我们找到最靠近质心的图像。 我们将这些图像称为代表性图像：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons

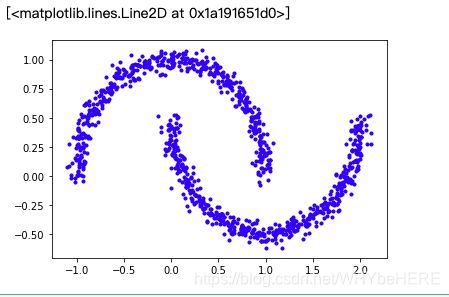
#构造数据集
X, y = make_moons(n_samples=1000, noise=0.05, random_state=42)

#画图
plt.plot(X[:,0],X[:,1],'b.')

结果输出：

#导入DBSCAN
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps = 0.05,min_samples=5)#设置eps 半径；min_sample 最小样本量
dbscan.fit(X)

dbscan.labels_[:10] #标签

dbscan.core_sample_indices_[:10] #核心对象索引，这里取前十个

np.unique(dbscan.labels_) #统计一共有多少个簇，-1是离群点，一共有0-6，7个簇

结果输出：

#画图
def plot_dbscan(dbscan, X, size, show_xlabels=True, show_ylabels=True):
    core_mask = np.zeros_like(dbscan.labels_, dtype=bool)
    core_mask[dbscan.core_sample_indices_] = True
    anomalies_mask = dbscan.labels_ == -1
    non_core_mask = ~(core_mask | anomalies_mask)

    cores = dbscan.components_
    anomalies = X[anomalies_mask]
    non_cores = X[non_core_mask]
    
    plt.scatter(cores[:, 0], cores[:, 1],
                c=dbscan.labels_[core_mask], marker='o', s=size, cmap="Paired")
    plt.scatter(cores[:, 0], cores[:, 1], marker='*', s=20, c=dbscan.labels_[core_mask])
    plt.scatter(anomalies[:, 0], anomalies[:, 1],
                c="r", marker="x", s=100)
    plt.scatter(non_cores[:, 0], non_cores[:, 1], c=dbscan.labels_[non_core_mask], marker=".")
    if show_xlabels:
        plt.xlabel("$x_1$", fontsize=14)
    else:
        plt.tick_params(labelbottom='off')
    if show_ylabels:
        plt.ylabel("$x_2$", fontsize=14, rotation=0)
    else:
        plt.tick_params(labelleft='off')
    plt.title("eps={:.2f}, min_samples={}".format(dbscan.eps, dbscan.min_samples), fontsize=14)

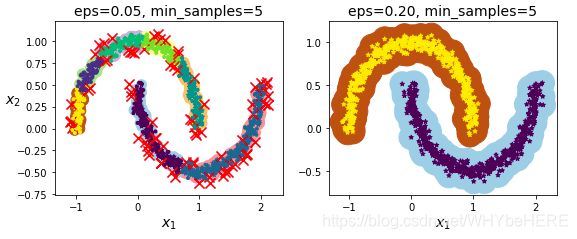
#画图
plt.figure(figsize=(9, 3.2))

plt.subplot(121)
plot_dbscan(dbscan, X, size=100)

plt.subplot(122)
plot_dbscan(dbscan2, X, size=600, show_ylabels=False)

plt.show()

结果输出：参数不同时的结果

参考链接

DBSCAN百度百科
数据科学中必须熟知的5种聚类算法