掌握经典排序算法( 类型一)由排名找最值
1. 前言
排序算法是计算机学科的基础内容。在工作中通常很少需要我们自己编写排序算法,很多开发库会提供相关接口,例如C++标准库,Qt等。既然开发库中有算法可以调用,为什么还要专门学习排序算法呢?主要有两点原因。第一,有些场景需要自行编写排序算法,这需要编程人员对算法有较好的了解。第二,应对考试,面试,排序算法是面试及考试的热点内容,有必要掌握。
常见的排序算法有十种,算法类型较多,靠死记硬背,很难记住。网络上有些文章采用了动画的方式进行演示,有助于理解单个算法的计算过程。实际上,各种排序算法之间并不是独立的,排序算法背后有着共通的设计思想和核心逻辑。掌握排序算法的核心逻辑,有助于理解算法的本质,从而更轻松地掌握这些算法,甚至达到自行设计算法的水平。
2. 认识排序
排序计算的本质是:
将数值大的数放在高地址位置,将数值小的数放在低地址位置。或者反过来,将数值大的数放在低地址位置,数值小的数放在高地址位置。其中,位置可以指索引,也可以指内存地址。
经典排序算法根据其计算特点,主要分为三种:
- 由排名找最值(最值法):先找排名第一的数据,再找排名第二的数据,再找排名第三的数据,依此类推,每一 轮计算都是从未确定排名的数据中取最值。相关算法有冒泡排序,选择排序,堆排序。
- 由数值找排名:从未排序的数组中取出一个数,在已排序队列中比较得到排名排名后插队。算法结束后,才能确定数据的最大值和最小值。例如插入排序。
- 整体局部排序法:先实现整体有序,再实现局部有序,或者先实现局部有序,再实现整体有序。算法结束后,才能确定数据的最大值和最小值。例如希尔排序,归并排序,快速排序,桶排序,计数排序,基数排序。
本篇主要讲最值法包含的排序算法。
3. 最值法
对于最值算法,首先要划分出两个数据区:
可能某个算法计算过程只有两个分区,也可能在算法的某个子步骤中也有两个分区。
当所有数据从无序区,移动到有序区,算法即结束。
3.1 冒泡排序
3.1.1 计算过程
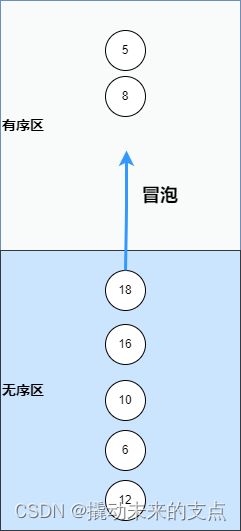
冒泡排序算法示意图如下:
无序区在下面,有序区在上面。
算法运行包括两个步骤:
- 使用冒泡法计算无序区最值。设当前数据指针指向无序区最底部的数,将当前数与其上方的数比较,如果此数小于上方的数,则将当前数和其上方的数交换位置,此操作即为冒泡。如果其上方的数小于当前的数,则将当前数据指针指向其上方的数。循环比较,直到当前数据成为无序区最顶部的数据,停止比较。此时,当前数据即为无序区最小的数,计算无序区最值的操作完成。
- 将最值追加到有序区底部。
重复上述步骤,直到所有的数据都进入有序区,算法结束。
简而言之,冒泡排序过程为:
从无序区中采用冒泡法得到最值,排到有序区的底部,直到无序区为空算法停止。
3.1.2 编码实现
示例代码使用Qt实现。项目地址:
- https://gitee.com/pivotfuture/SortAlgorithm/blob/master/src/bubbleSort/
示例代码中,我们用两种方式实现了冒泡排序。
- 一种是分配一个和待排序数组相同大小的新数组,将结果保存到新的数组中,待排序数组内容不变。核心代码如下:
/**
* @brief bubbleSort_putResultInNewArray
* 冒泡排序,结果存储在新数组中。原数组中数据不变。
* @param unordered_area 无序区数据指针
* @param data_count 需要排序的数据个数
*/
void bubbleSort_putResultInNewArray(int unordered_area[], size_t data_count)
{
if (data_count < 0) return;
// 申请有序区
int *ordered_area = (int *)malloc(data_count * sizeof(int));
// 当前未排序数据个数,初始化等于数据总数
int unordered_data_count = data_count;
// 当前有序区数据个数
int ordered_data_count = 0;
// 最外层循环为冒泡循环,直到所有的数据从无序区进入到有序区
for (int k = 0; k < data_count; k++)
{
// 内层循环为冒泡法计算最小值
// 当前数据指针默认指向第一个未排序的数据
int current_data_index = 0;
// 遍历无序区,使用冒泡法选出最值
for (int i = 1; i < unordered_data_count; i++)
{
// 当前数据引用
int ¤t_data = unordered_area[current_data_index];
// 当前数据上面的数据引用
int &upper_data = unordered_area[i];
// 如果当前数据小于其上面的数据,二者交换内容(即冒泡)
if (current_data < upper_data)
{
// 交换位置
int temp = upper_data;
upper_data = current_data;
current_data = temp;
// 向上冒泡,更新索引指向上面的位置
current_data_index = i;
}
// 如果二者相等,只需要将当前数据索引指向上面的一个数据
else if (current_data == upper_data)
{
current_data_index = i;
}
// 如果上面的数据更小,同样只需要将当前数据索引指向上面的一个数据
else
{
current_data_index = i;
}
}
// 此时无序区顶部为最小值
// 将最小值放到有序区底部
ordered_area[ordered_data_count] = unordered_area[unordered_data_count-1];
// 无序区数据个数减1
unordered_data_count--;
// 有序区数据加1
ordered_data_count++;
}
// 打印有序区
qDebug("在新数组中存储的结果为:");
for (int j = 0; j < ordered_data_count; j++)
{
printf("%d ", ordered_area[j]);
}
printf("\n");
// 删除有序区
free(ordered_area);
}
- 一种是将结果保存到原始数据中,原始数据会被结果数据覆盖。核心代码如下:
/**
* @brief bubbleSort_putResultInOriginArray
* 冒泡排序,结果存储在原数组中,原数组中数据会丢失。
* @param unordered_area 无序区数据指针
* @param data_count 需要排序的数据个数
*/
void bubbleSort_putResultInOriginArray(int unordered_area[], size_t data_count)
{
if (data_count < 0) return;
// 有序区和无序区公用一块内存,初始时,有序区指针指向无序区末尾
// 随着排序的进行,有序区底部向无序区顶部方向生长,无序区顶部向底部收缩
int *ordered_area = &unordered_area[data_count - 1];
// 当前未排序数据个数,初始化等于数据总数
int unordered_data_count = data_count;
// 当前有序区数据个数
int ordered_data_count = 0;
// 最外层循环为冒泡循环,直到所有的数据从无序区进入到有序区
for (int k = 0; k < data_count; k++)
{
// 内层循环为冒泡法计算最小值
// 当前数据指针默认指向第一个未排序的数据
int current_data_index = 0;
// 遍历无序区,使用冒泡法选出最值
for (int i = 1; i < unordered_data_count; i++)
{
// 当前数据引用
int ¤t_data = unordered_area[current_data_index];
// 当前数据上面的数据引用
int &upper_data = unordered_area[i];
// 如果当前数据小于其上面的数据,二者交换内容(即冒泡)
if (current_data < upper_data)
{
// 交换位置
int temp = upper_data;
upper_data = current_data;
current_data = temp;
// 向上冒泡,更新索引指向上面的位置
current_data_index = i;
}
// 如果二者相等,只需要将当前数据索引指向上面的一个数据
else if (current_data == upper_data)
{
current_data_index = i;
}
// 如果上面的数据更小,同样只需要将当前数据索引指向上面的一个数据
else
{
current_data_index = i;
}
}
// 此时无序区顶部为最小值,这同时也是有序区的底部
// 无序区数据个数减1
unordered_data_count--;
// 有序区数据加1
ordered_data_count++;
}
// 打印有序区
qDebug() << "在原数组中存储的结果为:";
for (int j = 0; j < ordered_data_count; j++)
{
// 这里最小值在有序区的顶部
printf("%d ", *(ordered_area - j));
}
printf("\n");
}
3.1.3 算法特点
冒泡排序过程中,数据交换位置的操作,需要大量地移动复制内存,会拖慢排序速度。减少内存移动复制,可以提高算法性能。
3.2 选择排序
3.2.1 计算过程
选择排序和冒泡排序非常相似。相对于冒泡排序,选择排序没有相邻数据两两交换的步骤。选择排序每轮计算,从未排序区选取一个最值,选取的方式不是冒泡法,而是比较选择法。
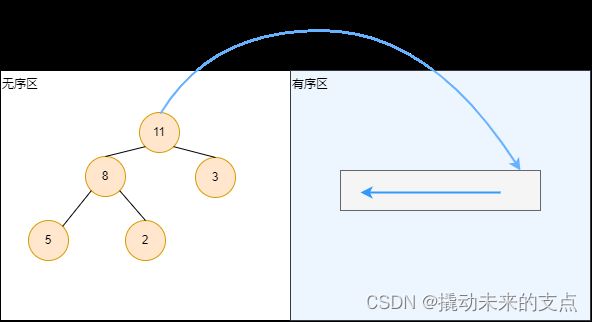
算法示意图如下:
计算过程:从未排序区选一个值,保存到一个临时变量中,作为比较过程的初始值,然后将临时变量逐个与未排序区中的剩余数据进行比较,并将较小/较大的数更新到临时变量中,并记录当前最值在未排序区的位置。当比较完成后,临时变量中的值即为整个未排序区的最值,此时需要将此值从未排序区中剔除掉。最后,将最值追加到有序区中即完成一次排序遍历。循环以上步骤,直到未排序区为空,排序结束。
简而言之,选择排序过程为:
从未排序区采用比较选择法取出最值,追加到有序区末尾,直到未排序区为空时算法结束。
3.2.2 编码实现
项目地址:
- https://gitee.com/pivotfuture/SortAlgorithm/tree/master/src/selectSort
示例项目中,我们对待排序数组进行了排序,并将结果保存到了待排序数组中。代码需要结合上面的算法示意图理解。核心代码如下:
/**
* @brief selectSort
* 选择排序,结果存储在原始数组中。
* @param unordered_area 无序区数据指针
* @param data_count 需要排序的数据个数
*/
void selectSort(int unordered_area[], size_t data_count)
{
if (data_count < 0)
return;
for (int k = 0; k < data_count; k++)
{
// 有序区左端指针
int *ordered_area_left = &unordered_area[data_count - k - 1];
// 取出一个数作为初始最小值
int minValue = unordered_area[0];
// 最小值索引
int min_value_index = 0;
// 未排序的数据个数
int unordered_count = data_count - k;
// 将基准数据和剩余未排序数据作比较
for (int i = 1; i < unordered_count; i++)
{
int unordered_value = unordered_area[i];
if (unordered_value < minValue)
{
minValue = unordered_value;
min_value_index = i;
}
}
// 最小值已取出到minValue中,将最小值右边的数据左移一位
for (int m = min_value_index; m < unordered_count - 1; m++)
{
unordered_area[m] = unordered_area[m + 1];
}
// 将最小值放入有序区左端
ordered_area_left[0] = minValue;
}
// 打印有序区
qDebug("排序后的数据为:");
for (int j = 0; j < data_count; j++)
{
printf("%d ", unordered_area[j]);
}
qDebug("(从右到左按从小到大的顺序排列)\n");
}
和冒泡排序一样,选择排序也可以将结果保存到新的数组中。另外还可以采用链表,列表容器等其他数据结构来优化程序,提高数据增删效率。
3.2.3 算法特点
相对于冒泡排序,选择排序内存交换更少,但从未排序区删除最值,会导致数据移动,编码实现时需要考虑使用合适的数据结构来提高运行效率。
3.3 堆排序
堆排序相对比较复杂。堆排序取最值的方法,采用了一定的数据结构,减少比较次数,提高找最值的效率。堆排序找最值使用的数据结构是完全二叉树。简单来说,完全二叉树是除了叶子层,其他层必须全满的二叉树,叶子层可以满,也可以不满。
与自然界中的树不同,数据结构中的树,通常画法是父节点在上,子节点在下,类似于金字塔堆的形状,所以这里我们也可以把树称作堆。如果堆中的父节点比左右子节点都大,则为大顶堆;如果堆中的父节点比左右子节点都小,则为小顶堆。
3.3.1 由数组建立大顶堆的示例
由数组建立大顶堆的过程图解如下所示:
- 必须是完全二叉树
- 父节点一定比子节点大,如果子节点比父节点大,子节点需要和父节点交换。
需要强调的是,大顶堆并不是一次性建立的,而是一个一个节点加入到树中并动态调整得到的。
可见,大顶堆最上方的根节点是最大值;同样小顶堆最上方的根节点是最小值。
3.3.2 计算过程
算法示意图如下:
堆排序计算过程描述如下:
- 首先建立大顶堆或小顶堆。
- 取出根节点中的最值,放入有序区左端。
- 将堆最后一个叶子节点,作为树的根节点,并对堆进行调整,使堆符合规则。
- 重复步骤2,3,直到无序区为空,算法结束。
3.3.3 编码实现
项目地址:https://gitee.com/pivotfuture/SortAlgorithm/tree/master/src/heapSort
核心代码如下:
/**
* @brief buildMaxHeap
* 将数组转为大顶堆。将数组转为大顶堆的过程其实就是一个调整节点位置求最值的过程。
* @param array
* int数组
* @param size
* 数组大小
*/
void buildMaxHeap(int array[], size_t size)
{
// 对于有n个节点的完全二叉树,只有前 n/2(向下取整) 个节点为父节点
// 我们只需要遍历n/2次,将所有最多三个节点的小树建立成大顶堆。
// 同时我们要从最后一个父节点,向前调整,也就是从底层父节点调整到
// 顶层父节点,这个过程和冒泡很相似。这样整个树就是一个大顶堆。
for (int i = size / 2 - ; i >= 0; i--)
{
adjustParentNode(array, size, i);
}
}
/**
* @brief adjustParentNode
* 调整堆的某个节点,确保父节点大于子节点。递归处理所有父节点即可。
* 对于有n个节点的完全二叉树,只有前 n/2(向下取整)个节点为父节点
* @param array
* @param size
* @param parentIndex
*/
void adjustParentNode(int array[], size_t size, int currentParentIndex)
{
int leftChildIndex = currentParentIndex * 2 + 1; // 左孩子索引
int rightChildIndex = leftChildIndex + 1; // 右孩子索引
int maxValueIndex = currentParentIndex; // 最大值索引,默认指向当前父节点
// 左孩子不一定真实存在,这里需要进行检测
if (leftChildIndex < size)
{
// 左节点和根节点比较,记录较大值的索引
if (array[leftChildIndex] > array[currentParentIndex])
{
maxValueIndex = leftChildIndex;
}
}
// 右孩子不一定真实存在,这里需要进行检测
if (rightChildIndex < size)
{
if (array[rightChildIndex] > array[maxValueIndex])
{
maxValueIndex = rightChildIndex;
}
}
// 如果父节点比其孩子节点小
if (maxValueIndex != currentParentIndex)
{
// 交换二者,使父节点位置的值为最大值
swap(array[maxValueIndex], array[currentParentIndex]);
}
else
{
// 否则不动
}
}
/**
* @brief swap
* 数据交换函数
* @param a
* @param b
*/
void swap(int &a, int &b)
{
int temp = a;
a = b;
b = temp;
}
/**
* @brief heapSort
* 堆排序,结果存储在原数组中
* @param unordered_area 无序区数据指针
* @param data_count 需要排序的数据个数
*/
void heapSort(int unordered_area[], size_t data_count)
{
if (data_count < 0)
return;
// 记录未排序数据个数
int unordered_data_count = data_count;
// 建立大顶堆,数组第一个元素即为最大值
buildMaxHeap(unordered_area, data_count);
// 只需要遍历data_count - 1次,最后一个未排序的数,自己构成大顶堆,此时什么也不用做。
for (int i = 0; i < data_count - 1; i++)
{
// 将最大值和未排序区末尾的值交换,此时最大值成为有序区的一部分,无序区数值个数减1。
swap(unordered_area[0], unordered_area[unordered_data_count - 1]);
// 无序区数值个数减1
unordered_data_count--;
// 末尾值成为当前未排序区的树根,此时树不再是大顶堆,需要重新建立大顶堆。
buildMaxHeap(unordered_area, unordered_data_count);
}
// 此时无序区大小为0,有序区大小为data_count
// 打印有序区
qDebug("堆排序后的数据为:");
for (int j = 0; j < data_count; j++)
{
printf("%d ", unordered_area[j]);
}
printf("\n");
}
代码注释比较详细,对着代码调试能够更好的理解。
3.3.4 算法特点
以大顶堆为例,较大的值总是在上面,所以每次找最值相对更容易,不需要将全部元素遍历一遍,减少了遍历次数,理论上提高了排序效率。
4. 平均时间复杂度比较
冒泡排序、选择排序,每次计算最大值,都需要遍历一次无序区。对n个待排序数,第m次遍历次数为n-m,总共要遍历n-1次,所以总的遍历次数为:
( n − 1 ) + ( n − 2 ) + . . . + 1 = ( n − 1 ) n 2 (n-1)+(n-2)+...+1=\frac{(n-1)n}{2} (n−1)+(n−2)+...+1=2(n−1)n
转为平均时间复杂度,只需要看n的函数类型,这里为平方函数,所以冒泡和选择排序的数量级是 n 2 n^2 n2,即平均时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
堆排序平均时间复杂度计算比较复杂,为 O ( n l o g 2 n ) O(nlog_2 n) O(nlog2n)。计算过程大家可以自行查阅相关资料。堆排序理论上更加高效,而建堆的过程确实会消耗一些计算资源,实际应用中不可忽视,需要考虑。
5. 结语
本文讲解了最值法的相关排序算法。所有排序算法都可以进行优化,只要掌握其原理,每个人都可以对算法过程进行分析,提出优化改进方案。
下一篇我们研究由数值找排名相关排序算法。
本文原创发布于Qt未来工程师,后续内容已在公众号中发布,敬请关注。