2-4基础算法-离散化/贪心/01背包问题
文章目录
- 一.离散化
- 二.贪心
- 01背包问题
一.离散化
离散化是一种将数组的值域压缩,从而更加关注元素的大小关系的算法。
离散化数组要求内部有序(一般去重)
可以通过离散化下标得到值
也可以通过值得到离散化下标

#include 二.贪心
分析:先进行排序,从某个位置划分,左侧是a,右侧是b。则max a和min b是相邻的。只需计算相邻两数的差最小值
#include 分析:贪心:每次选择最小的两个部落合并
#include 或优先队列
#include 评测系统
#include 或
#include 4.分糖果

解读:
①字典序:apple排在banana前面,我们认为apple的字典序更小
②假设我们有6个糖果分给3个学生,可能的分法是:ab、cd、ef,则拿到ef的同学字典序最大
③使得字典序最大的字符串尽可能小:指的是字典序最大的字符串的字典序最小,而不是长度最短(除非只有一个种类的糖果)。一种可能的分法中,字典序最大的是abccd;另一种分法中,字典序最大的是d。我们会选择abccd这种分法作为最终结果
分析:
糖果的种类数可能有三种情况
①只有一个种类的糖果:应使分的字典序最大的(分的糖果数最多的)同学拿到的糖果尽可能少(字符串尽可能小)。也就是尽可能的均分。如我们有7个糖果,分为3个同学。应该是2/2/3的分法
②一共有n个糖果,分给x个同学。我们先将输入序列s排序,现在同种类的糖放在了一起。若第x个糖果的种类和第1个糖果的种类不一样。 我们将前x个糖果依次分给x个同学,则第x个同学拿到了字典序最大的,又由于序列是有序的,x对应的字典序一定是当前最小的。从x+1到n(若有)的糖果我们将其分给第一位同学,因为第一位同学的首字母一定小于第x位同学,所以该操作不会产生影响。
③一共有n个糖果,分给x个同学。我们先将输入序列s排序,现在同种类的糖放在了一起。**若第x个糖果的种类和第1个糖果的种类一样。**这时,第x个糖果的字典序一定是最小的(因为已经排序),我们直接输出[x,n]即为最终序列。如:aaaabbbbcccc,4人,显然最佳分配a/a/a/abbbbcccc>其他分配abbb/a/a/accc
#include 评测系统
注:最多进行k次,并非一定要进行k次
#include 分析:先求和,然后奇数位找最小的,偶数位找最大的,交换。
#include #include 8.四个瓷瓶的神秘游戏
评测系统
分析:当一个瓶子为空的时候,我们依然可以继续操作。当两个瓶子都为空的时候,我们无法操作。
在通过sort排序后,满足a[0]<=a[1]<=a[2]<=a[3]。我们先通过操作将a[0]变为空,可操作次数为a[0]内的珍珠数。此时最后一个瓶内珍珠数最多,为a[3]+2*a[0]
在此基础上,对其他瓶进行处理
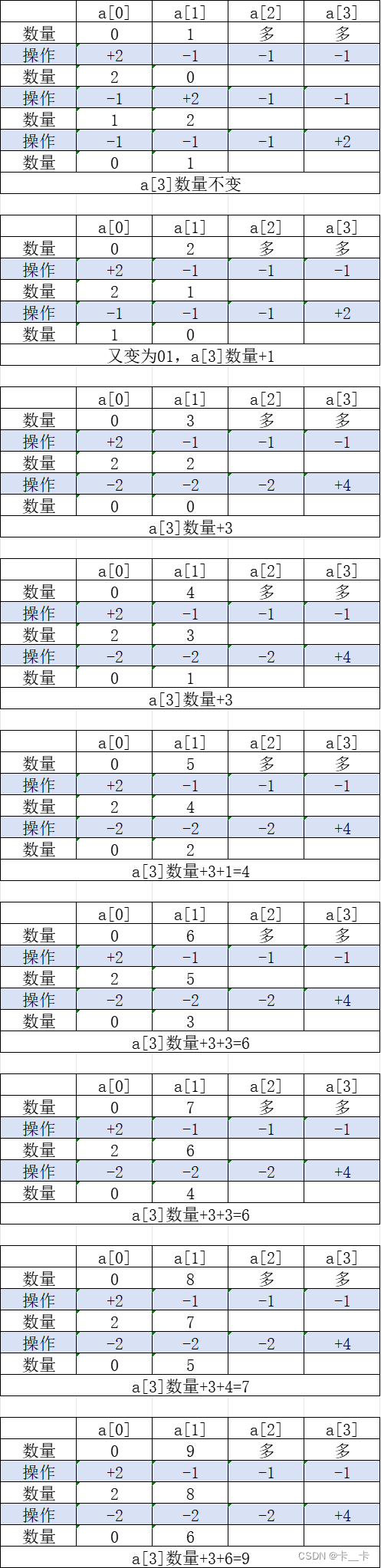
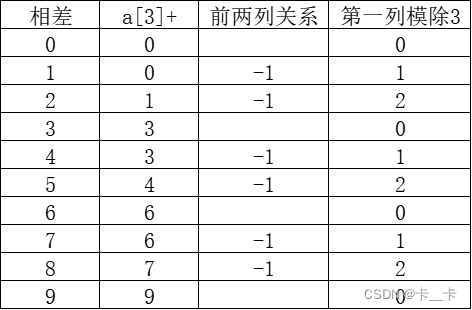
因为a[2]不小于a[1],所以能对a[1]进行的操作都可以对a[2]进行操作,我们假设a[2]和a[3]足够大。我们分别假设在a[0]为0时,a[1]分别取1~9,于是有:
以此类推,我们可以总结出
可以看出,相差模除为0时,a[1]和a[0]的差值就是a[3]要增加的值;差值模除为其他时,a[3]要增加的值为a[1]和a[0]的差值-1
于是有
#include 下面考虑a[3]或a[2]非足够大的情况,拥有最多珍珠的瓶子可能就不是a[3]:
在将a[0]变为0的基础上:
当瓶子内珍珠数为0111时,一次操作变为2000,此时瓶内最多珍珠数量为2,但按上述分析前两个瓶01时,a[3]数量不变,也就是1,和2差1
当瓶子内珍珠数为0112时,一次操作变为2001,此时瓶内最多珍珠数2,a[3]数量不变也正好是2,满足上述推理
当瓶子内珍珠数为0113时,一次操作变为2002,此时a[0]=2,a[3]数量不变为3,此时a[3]成为珍珠最多的瓶
当瓶子内珍珠数为0222时,一次操作变为4000,此时瓶内最多珍珠数4,但按上述分析前两个瓶02时,a[3]数量+1,也就是3,和4差1
以此类推
可以看出,当a[3]不是足够大时,或者说,a[3]如果不满足至少比a[2]或a[1]大1时,即a[1]、a[2]、a[3]相等时,a[0]反而成了珍珠最多的瓶
我们据此更新代码,考虑a[1]、a[2]、a[3]相等的情况,要在输出基础上+1
#include 分析:商品价格有正有负,计算过程中可抵消
#include 评测系统
分析:样例说明有一定的误导性,为了更高效的派出冒险者,应该从小到大排序
#include 评测系统
分析:在一轮中所有队员均可上场;对每个队员至多需要一次付费
引入:
01背包问题
对于一系列物品,每个物品有两个属性,价值v[i]和重量w[i];一个背包,它有一个最大承重限制W。在0-1背包问题中,每个物品只有两种状态:被选中和未被选中,这就是"0-1"的由来。不同于分数背包问题,我们不能选择物品的一部分,而必须决定是否完整地取用每个物品。0-1背包问题通常通过动态规划来解决。基本思想是使用一个二维数组dp[i][j]来表示当考虑到前i个物品,且背包容量为j时所能得到的最大价值。
我们的目标是选择一些物品装入背包,使得这些物品的总价值最大化,同时保证这些物品的总重量不超过背包的承重限制。

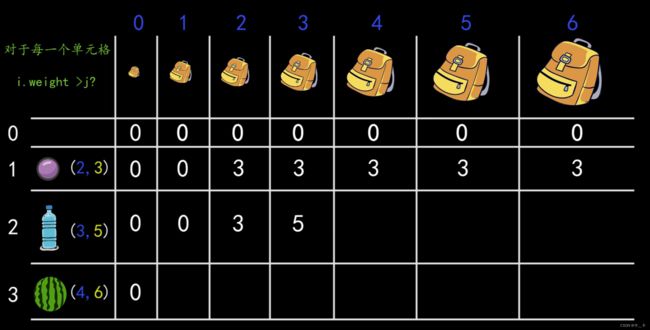
物品(重量w,价值v)
第0行:不考虑任何物品,背包的最大价值为0
第0列:当背包重量为0时,无法放入任何物品,最大价值为0
表格中的每个数字都表示:当考虑前i个物品时,在背包重量j下,能获得的最大价值

对于[1,1]
背包容量为1,1号物品重量为2,无法放入背包。
即当前物品重量大于背包容量,则背包价值与不放当前物品的价值一致(与只考虑前i-1个物品一致)
if(weight[i]>j){
dp[i][j]=dp[i-1][j]
}
对于[2,3]
当前物品重量为3≤当前背包容量3,允许放入
判断放入后是否能获得更大价值:max(不放入,放入)
若不放入:背包的最大价值=在同样的背包容量j下,能获得的最大价值,即dp[i-1][j]
若放入:背包内物品的总重量一定已经加上了当前物品的重量和价值,我们找到"不考虑当前物品的价值"和“减去当前物品重量”对应的最优值,再加上当前物品的价值,即可得到结果,即dp[i-1][j-weight[i]]+value[i]
if(weight[i]<=j){
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
}
对于另一个例子,我们给出完整的代码(注:weight和value数组下标从1开始存放数据,0号索引填充0)
这里使用vector表示,也可使用数组
#include >创建二维数组
//外层(行)有n + 1个元素(向量)
//对于每个外层元素都有W+1个内层元素(列),并将它们初始化为0
vector<vector<int>> dp(n + 1, vector<int>(W + 1, 0));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= W; j++) {
if (weight[i] <= j) {
dp[i][j] = max(dp[i-1][j], dp[i - 1][j - weight[i]] + value[i]);
}
else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[n][W];
}
int main() {
int W = 10;//背包最大容量
vector<int> weight = { 0,1,2,4,2,5 };//每个物品的重量
vector<int> value = { 0,5,3,5,3,2 };//每个物品的价值
cout << knapsack(W, weight, value);//在不超过背包承重限制的条件下,所能选择物品的最大总价值。
}
下面我们再看一个一维dp的例子
一维dp每次迭代只保留上一个物品计算的结果,减少了对空间的需求,空间复杂度有所降低。如果问题只要求最大价值而不需要具体的物品列表,一维DP是更好的选择。如果需要知道具体哪些物品被选中,则可能需要额外的逻辑或记录。二维dp可以具体到每个物品和每种容量下的最大价值。
若背包容量10,共有4件物品,(重量,价值)分别为(2,1),(3,3),(4,5),(7,9)
处理第一个物品:从右往左填写。第一个物品重量2<10,允许放入,直到j=2。检查价值最大化。
for (int j = W; j >= weight[i]; j--) { //逆序保证了在更新时用到的dp仍然是上一轮(没有考虑当前物品)的结果
dp[j] = max(dp[j], dp[j - weight[0]] + value[0]);
}
处理第二个物品:j=10前两件物品均可放入
j=4时
若不放入当前物品,dp[j]=1
若放入当前物品,在减去当前重量的情况下决策dp[j - weight[1]] + value[1]=0+3=3
for (int j = W; j >= weight[i]; j--) {
dp[j] = max(dp[j], dp[j - weight[1]] + value[1]);
}
对于另一个例子,我们给出完整的代码(注:weight和value数组下标从0开始存放数据),j是逆序的
这里使用vector表示,也可使用数组
#include 【回到题目】我们使用01背包一维dp找到最大的攻击力,再找到最多血量的敌人,即可计算最小的回合数
#include