【笔记 ing】计算机网络-网络安全基本原理-密码学基础

计算机之危机四伏

本讲主题

密码学基础

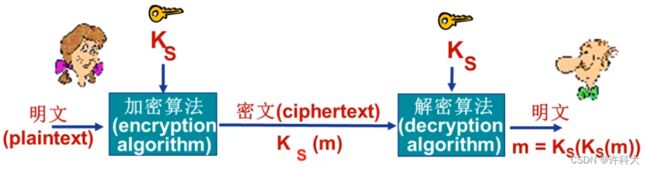
密码学（cryptography）术语

明文plaintext

加密算法encryption algorithm

密文ciphertext

解密decryption

解密算法decryption algorithm

m：明文
$K_A$(m)：密文，利用秘钥$K_A$加密

m=$K_B$($K_A$(m))：利用秘钥$K_B$解密

对称密钥加密

对称密钥加密：Bob和Alice共享相同（对称）秘钥：$K_S$
e.g.,单码替代密码的替代模式
Q：Bob和Alice如何确认秘钥值（秘钥分发）？

公开密钥加密

破解加密方法

1、唯密文攻击（cipher-text only attack），基于对密文的分析进行破解
两条路径：
暴力破解（brute force）：尝试所有可能的秘钥
统计分析
2、已知明文攻击（known-plaintext attack）：入侵者已知（部分）明文以及与之匹配的密文
e.g.,在单码替代密码（monoalphabetic cipher）中，入侵者已确认字母a,l,i,c,e,b,o的替换关系
3、选择明文攻击（chosen-plaintext attack）：入侵者可以获取针对选择的明文的密文

传统加密方法

替代密码（substitution cipher）：利用一种东西替代另一种东西
1、凯撒密码（Casesar cipher）：一个字母替代另一个字母
将一个字母利用字母表中该字母后面的第k个字母替代
如k=3，bob,i love you.alice -> ers,l oryh brx.dolfh
2、单码替代密码（monoalphabetic cipher）
明文：abcdefghijklmnopqrstuvwxyz
密文：mnbvcxzasdfghjklpoiuytrewq
e.g.,明文：bob,i love you.alice
密文：nkn,s gktc wky.mgsbc
加密秘钥：26个字母集合向26个字母集合的映射
3、多码（字母）替代加密（polyalphabetic cipher）：使用多个单码替代密码，明文中不同位置的字母使用不同的单码替代密码
例如，采用两个凯撒密码的多码替代加密：
Plaintext letter:abcdefghijklmnopqrstuvwxyz
$C_1$(k=5):fghijklmnopqrstuvwxyzabcde
$C_2$(k=19):tuvwxyzabcdefghijklmnopqrs
加密秘钥:($C_1$(k=5),$C_2$(k=19));$C_1$,$C_2$,$C_2$,$C_1$,$C_2$;…
明文：bob,i love you.
密文：ghu,n etox dhz.

换位（transpositions）密码：重新排列明文中的字母
1、置换法（permutation method）
将明文划分为固定长度（d）的组，每个组内的字母按置换规则（f）变换位置
秘钥：（d,f）
例如：
秘钥：d=4,f:=(1->3,2->1,3->4,4->2)

明文（m）：i love you
=》ilov eyou
密文（c）：lvioyueo
2、列置换加密
将明文按行组成一个矩阵，然后按给定列顺序输出得到密文
例如：
秘钥：k=4（矩阵列数），（2,3,1,4）（输出顺序）
明文（m）：bob,i love you.
加密
列数：k=4
b o b i
l o v e
y o u x
密文（c）：
按序（2,3,1,4）输出每列：
2 ooo
3 bvu
1 bly
4 iex
ooobvublyiex
解密
$\lceil$$\frac{length(c)}{k}$$\rceil$=3
列数：k=3
顺序：2,3,1,4
b l y
o o o
b v u
i e x
bobiloveyoux


列置换加密的秘钥包括列数和输出顺序
可以用一个单词来表示
单词长度表示列数，单词中的字母顺序表示输出顺序
例如：
秘钥：nice
明文（m）：bob i love you
加密：
k=4，顺序：cein：3421
bobi
love
youx
密文：bvuiexooobly
解密：
k=length/k=3,顺序：
1 bly 4
2 ooo 3
3 bvu 1
4 iex 2
bobiloveyou

现代加密技术

1、现代加密技术的基本操作包括经典的替代和置换
不再针对一个个字母，而是针对二进制位操作
2、现代加密技术主要分为：
对称秘钥加密
非对称密钥加密（公开密钥加密）
3、对称密钥加密
流密码（stream ciphers）
分组密码，也称块密码（block ciphers）

流密码

基本思想
首先利用秘钥K产生一个秘钥流：z=$z_0$$z_1$$z_2$
然后使用如下规则对明文串x=$x_0$$x_1$$x_2$…加密：
y=$y_0$$y_1$$y_2$…=$E{z}_0$($x_0$)$E{z}_1$($x_1$)$E{z}_2$($x_2$)
解密时，使用相同的秘钥流与密文做运算（XOR）

流密码工作流程

分组密码

将明文序列划分成长为m的明文组
各明文组在长为i的秘钥组的控制下变换成长度为n的密文组
通常取n=m
n>m扩展分组密码
n 典型分组密码结构：Feistel分组密码结构
在设计密码体制的过程中，Shannon提出了能够破坏对密码系统进行各种统计分析攻击的两个基本操作：扩散（diffusion）和混淆（confussion）
基于1949年Shannon提出的交替使用替代和置换方式构造密码体制

Feistel分组密码结构

基于“扩散”和“混乱”的思考，Feistel提出通过替代和置换交替操作方式构造密码
Feistel是一种设计原则，并非一个特殊的密码
加密：
将明文分为左、右两部分：
明文=（$L_0$,$R_0$）
每一轮i=1,2,…,n，计算：
$L_i$=$R_{i-1}$
$R_i$=$L_{i-1}$ $⨁$ F($R_{i-1}$,$K_i$)
其中F是轮函数；$K_i$是子密钥
解密：
密文=($L_n$,$R_n$)
每一轮i=n,n-1,…,1计算：
$R_{i-1}$=$L_i$
$L_{i-1}$=$R_i$ $⨁$ F($R_{i-1}$,$K_i$)
其中F是轮函数，$K_i$是子密钥
密文=($L_0$,$R_0$)

// 注：下图的$K_0$,$K_n$可能不太正确，下图的加密过程密钥K对应的下标n可能应为1->n+1，下图的解密过程密钥K对应的下标n可能应为n+1->1

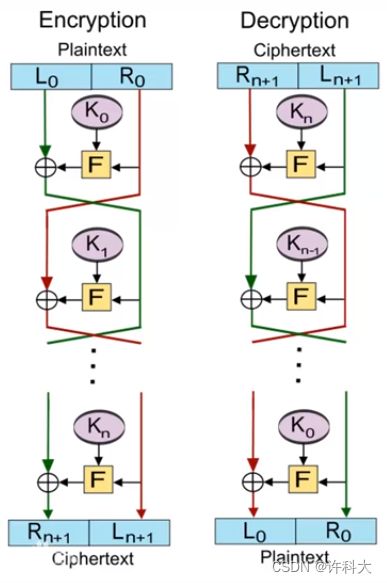
Feistel结构的分组密码安全性取决于：
1、分组长度
分组长度越大，安全性越高，加密速度越慢，效率越低
目前常用的分组加密算法的分组长度取64位
2、子密钥的大小
子密钥长度增加，安全性提高，加密速度降低
设计分组密码时需要在安全性和加密效率之间进行平衡
3、循环次数
循环越多，安全性越高，加密效率越低
4、子密钥产生算法
在初始秘钥给定的情况下，产生子密钥的算法越复杂，安全性越高
5、轮函数
一般情况下，轮函数越复杂，机密算法的安全性越高

数据加密标准：DES

DES：Data Encryption Standard
IBM公司研制
1972年，美国国家标准局NBS（National Bureau of Standards）开始实施计算机数据保护标准的开发计划
1973年5月13日，NBS征集在传输和存储数据中保护计算机数据的密码算法
1975年3月17日，首次公布DES算法描述
1977年1月15日，正式批准为加密标准（FIPS-46），当年7月1日正式生效
1994年1月的评估后决定1998年12月以后不再将DES作为数据加密标准
DES是16轮的Feistel结构密码
DES是一个包含16阶段的“替代-置换”的分组加密算法
DES的分组长度是64位：64位的分组明文序列作为加密算法的输入，经过16抡加密得到64位的密文序列
DES使用56位的密钥
DES的每一轮使用48的子密钥：每个子密钥是56位密钥的子集构成

DES算法结构

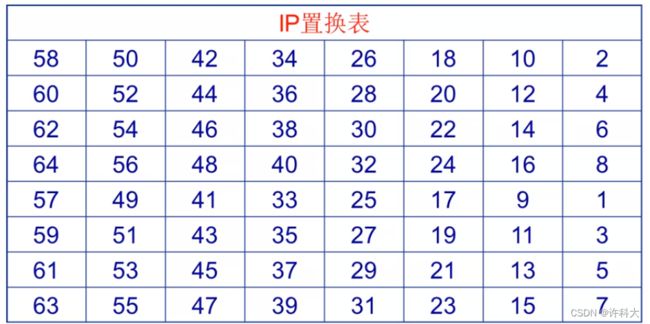
初始置换IP（Initial Permutation）

把输入的64位的排列顺序打乱，每位数据按照下列规则重新组合

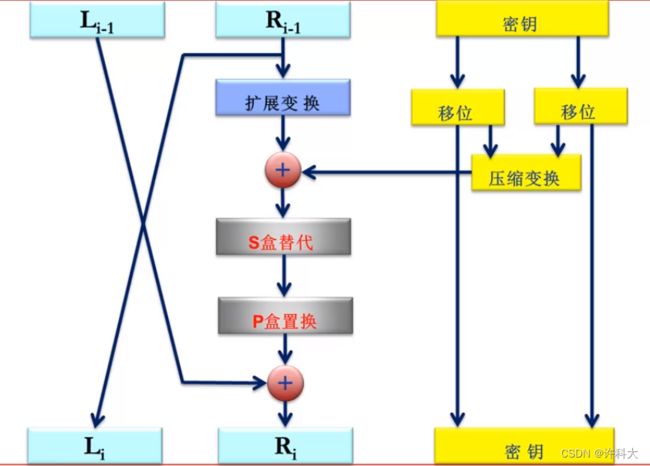
一轮DES加密过程

DES：f函数结构

黑盒变换
多个函数/操作（E扩展、异或、S替代、P置换）的组合函数

f函数的基本操作

扩展变换：扩展变换（Expansion Permutation，也被称为E-盒）将64为输入序列的右半部分从32位扩展到48位
确保最终的密文与所有的明文位都有关

S-盒替代（X-boxes Substitution）
6bit->4bit

P盒置换（P-boxes Permutation）

逆初始置换（Inverse Initial Permutation）

初始置换和对应的逆初始置换操作并不会增强DES算法的安全性
主要目的是为了更容易地将明文和密文数据以字节大小放入DES芯片中

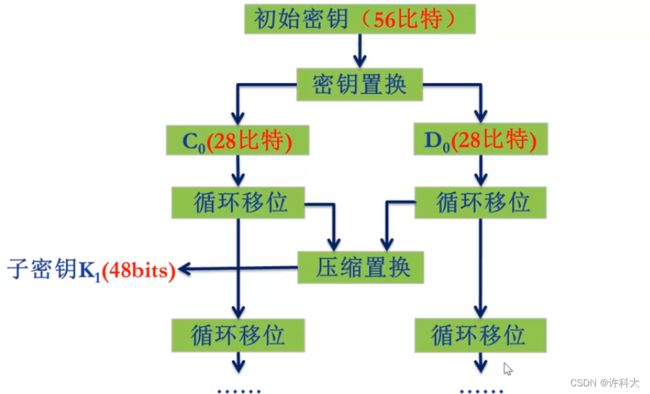
每轮子密钥的生成

————————————

仅用于本人学习

来源：中国大学慕课-计算机网络-哈尔滨工业大学-李全龙、聂兰顺