【详解】求解迷宫所有路径(递归实现)----直接打穿迷宫
目录
递归的模型:
栈帧:
递归调用深度:
编辑
用递归算法求解迷宫问题:
小结:
结语:
递归的小小总结,朋友们可以看看,有助于理解后面的递归程序。
递归的模型:
递归模型由递归出口和递归体两部分组成,递归出口即递归的结束条件,递归体确定递归求解时的递推关系。
这两步缺一不可,没出口会死循环,没有递归体求解不出答案。(建议大家做递归题时一定要在纸上把这两个写出来,递归代码实现不难,难的是思路)
栈帧:
单个函数调用操作所使用的函数调用栈被称为栈帧结构简单来说就是每个栈帧对应着一个未运行完的函数。栈帧中保存了该函数的返回地址和局部变量。
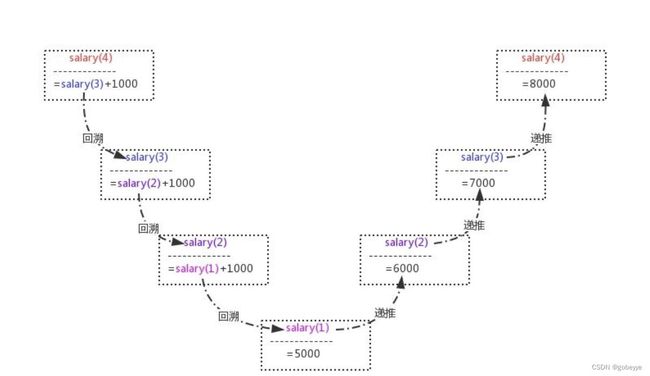
递归调用深度:
类似于这样的递归调用深度为4,其实就是大问题化到递归出口需要调用递归函数的次数。
深度不能太大,会栈溢出。
用递归算法求解迷宫问题:
自定义PathType来存储每一步的数据
Box为每个点的数据类型
用count来存储一共有几条路可以走
大部分解析都在代码里面了,我这里就不多叙述。
typedef struct
{
int i; //当前方块的行号
int j; //当前方块的列号
} Box;
typedef struct
{
Box data[MaxSize];
int length; //路径长度
} PathType; //定义路径类型
int count=0; //存放迷宫路径的条数求解迷宫函数mgpath参数xi,yi为当前的坐标,xe,ye为迷宫出口的坐标,path用来保存每一步,一但找到出口就把path输出(path其实是顺序表结构),可能有的朋友不太懂为什么要回退,这是因为我们要找迷宫的所有出口,进行回溯,这样递归就能进行全部查找,和树差不多(由于这样的空间消耗很大,和时间复杂度较高,所以迷宫不适合太大)。
void mgpath(int xi,int yi,int xe,int ye,PathType path)
//求解路径为:(xi,yi)->(xe,ye)
{
int di,k,i,j;
if (xi==xe && yi==ye) //找到了出口,输出路径
{
path.data[path.length].i = xi;
path.data[path.length].j = yi;
path.length++;
printf("迷宫路径%d如下:\n",++count);
for (k=0;k总代码:
#define _CRT_SECURE_NO_WARNINGS 1
//【例5.5】的算法:递归算法求解从入口到出口的所有迷宫路径
#include
#define MaxSize 100
#define M 4
#define N 4
int mg[M+2][N+2]={ {1,1,1,1,1,1},{1,0,0,0,1,1},{1,0,1,0,0,1},{1,0,0,0,1,1},{1,1,0,0,0,1},{1,1,1,1,1,1} };
typedef struct
{
int i; //当前方块的行号
int j; //当前方块的列号
} Box;
typedef struct
{
Box data[MaxSize];
int length; //路径长度
} PathType; //定义路径类型
int count=0; //存放迷宫路径的条数
void mgpath(int xi,int yi,int xe,int ye,PathType path)
//求解路径为:(xi,yi)->(xe,ye)
{
int di,k,i,j;
if (xi==xe && yi==ye) //找到了出口,输出路径
{
path.data[path.length].i = xi;
path.data[path.length].j = yi;
path.length++;
printf("迷宫路径%d如下:\n",++count);
for (k=0;k 小结:
递归问题一般都要先把解题思路想好,再进行解答,有时递归的深度比较大,可能要自己转换为递推形式,然后就相信函数,相信自己,有一些小细节不必深究(不然你可能就会陷入无穷的细节无法自拔)。
结语:
其实写博客不仅仅是为了教大家,同时这也有利于我巩固自己的知识点,和一个学习的总结,对文章有任何问题的还请指出,接受大家的批评,让我改进,如果大家有所收获的话还请不要吝啬你们的点赞和收藏,这可以激励我写出更加优秀的文章。