强化学习—模仿学习 行为克隆 生成式对抗网络模型
第十五章 模仿学习
15.1 简介
虽然强化学习不需要有监督学习中的数据标签,但它十分依赖奖励函数的设置。有时在奖励函数上做一些微小的改动,训练出来的策略就会天差地别。在很多现实场景中,奖励函数并未给定,或者奖励信号及其稀疏,此时随机设计奖励函数将无法保证强化学习训练出来的策略满足实际需要。例如,对于无人驾驶车辆智能体的规控,其观测是当时的环境感知恢复的3D局部环境,动作是车辆接下来数秒的具体路径规划,那么奖励是什么?如果只是规定正常行驶而不发生碰撞的奖励为+1,发生碰撞为-100,那么智能体学习的结果则很可能是找个地方停滞不前。具体能帮助无人驾驶小车规控的奖励函数往往需要专家的精心设计和调试。
假设存在一个专家智能体,其策略可以看成最优策略,我们就可以直接模仿这个专家在环境中交互的状态动作数据来训练一个策略,并且不需要用到环境提供的奖励信号。模仿学习研究的便是这一类问题,在模仿学习的框架下,专家能够提供一系列状态动作对 { ( s t , a t ) } \left\{(s_t,a_t)\right\} {(st,at)},表示专家在 s t s_t st环境下做出了 a t a_t at的动作,而模仿者的任务则是利用这些专家数据进行训练,无须奖励信号就可以达到一个接近专家的策略。目前学术界模仿学习的方法基本上可以分为三类:
- 行为克隆(BC)
- 逆强化学习(RL)
- 生成式对抗模仿学习(GAIL)
在本章将主要介绍行为克隆方法和生成式对抗模仿学习方法。尽管逆强化学习有良好的学术贡献,但由于其计算复杂度较高,实际应用价值较小。
15.2 行为克隆
行为克隆(BC)就是直接使用监督学习方法,将专家数据中 ( s t , a t ) (s_t,a_t) (st,at)的 s t s_t st看作样本输入, a t a_t at视为标签,学习的目标为
θ ∗ = a r g m i n θ E ( s , a ) B [ L ( π θ ( s ) , a ) ] \theta^*=arg\text{}\underset{\theta}{min} \mathbb E_{(s,a)~B}[\mathcal L(\pi_\theta(s),a)] θ∗=argθminE(s,a) B[L(πθ(s),a)]
其中,B是专家数据集, L \mathcal L L是对应监督学习框架下的损失函数。若动作是离散的,该损失函数可以是最大似然估计得到的。若动作是连续的,该损失函数可以是均方误差函数。
在训练数据量比较大的时候,BC能够很快地学习到一个不错的策略。例如,围棋人工智能AlphaGo就是首先在16万盘棋局的3000万次落子数据中学习人类选手是如何下棋的,仅仅凭借这个行为克隆方法,AlphaGo的棋力就已经超过了很多业余围棋爱好者。由于BC的实现十分简单,因此在很多实际场景下他都可以作为策略预训练的方法。BC能使得策略无须在较差时仍然低效地通过和环境交互来探索较好的动作,而是通过模仿专家智能体的行为数据来快速达到较高水平,为接下来的强化学习创造一个高起点。
BC也存在很大的局限性,该局限性在数据量比较小的时候犹为明显。具体来说,由于通过BC学习得到的策略只是拿小部分专家数据进行训练,因此BC只能在专家数据的状态分布下预测的比较准。然而,强化学习面对的是一个序贯决策问题,通过BC学习得到的策略在和环境交互过程中不可能完全学成最优,只要存在一点偏差,就有可能导致下一个遇到的状态是在专家数据中没有见过。此时,由于没有在此状态(或者比较相近的状态)下训练过,策略可能就会随机选择一个动作,这会导致下一个状态进一步偏离专家策略遇到的数据分布。最终,该策略在真实环境下不能得到比较好的效果,这被称为行为克隆的复合误差问题。
15.3 生成式对抗模仿学习
生成式对抗模仿学习(GAIL)是2016年由斯坦福大学研究团队提出的基于生成式对抗网络的模仿学习,他诠释了生成式对抗网络的本质其实就是模仿学习。GAIL实质上是模仿了专家策略的占用度量 ρ E ( s , a ) \rho_E(s,a) ρE(s,a),即尽量使得策略在环境中的所有状态对 ( s , a ) (s,a) (s,a)的占用度量 ρ π ( s , a ) \rho_\pi(s,a) ρπ(s,a)和专家策略的占用度量一致。为了达成这个目标,策略需要和环境进行交互,收集下一个状态的信息并进一步做出动作。这一点和BC不同,BC完全不需要和环境交互。GAIL算法中有一个判别器和一个策略,策略 π \pi π就相当于是生成式对抗网络中的生成器,给定一个状态,策略会输出这个状态下应该采取的动作,而判别器D将状态动作对 ( s , a ) (s,a) (s,a)作为输入,输出一个0到1之间的实数,表示判别器认为该状态动作对 ( s , a ) (s,a) (s,a)是来自智能体策略而非专家的概率。判别器D的目标是尽量将专家数据的输出靠近0,将模仿者策略的输出靠近1,这样就可以将两组数据分辨开来。于是判别器D的损失函数为
L ( Φ ) = − E ρ π [ l o g D Φ ( s , a ) ] − E ρ E [ l o g ( 1 − D Φ ( s , a ) ) ] \mathcal L(\varPhi )=-\mathbb E_{\rho_\pi}[logD_\varPhi(s,a)]-\mathbb E_{\rho_E}[log(1-D_{\varPhi}(s,a))] L(Φ)=−Eρπ[logDΦ(s,a)]−EρE[log(1−DΦ(s,a))]
其中 Φ \varPhi Φ是判别器D的参数。有了判别器D之后,模仿者策略的目标就是其交互产生的轨迹能被判别器误认为专家轨迹。于是,我们可以用判别器D的输出来作为奖励函数来训练模仿者策略。具体来说,若模范者策略在环境中采样到状态 s s s,并且采取动作 a a a,此时该状态动作对 ( s , a ) (s,a) (s,a)会输入到判别器D中,输出 D ( s , a ) D(s,a) D(s,a)的值,然后将奖励设置为 r ( s , a ) = − l o g D ( s , a ) r(s,a)=-logD(s,a) r(s,a)=−logD(s,a) (当判别器输出越靠近0奖励值越大,输出越靠近1奖励值越小)。于是,我们可以用任意强化学习算法,使用这些数据继续训练模仿者策略。最后,在对抗过程不断进行后,模仿者策略生成的数据分布将接近真实的专家数据分布,达到模仿学习的目标。GAIL的优化目标如图15-2所示。
第三章介绍过一个策略和给定MDP交互的占用度量呈一一对应的关系。因此,模仿学习的本质就是通过更新策略使其占用度量尽量靠近专家的占用度量,而这正是GAIL的训练目标。由于一旦策略改变,其占用度量就会改变,因此为了训练好最新的判别器,策略需要不断和环境做交互,采样出最新的状态对样本。
15.4 代码实践
15.4.1 生成专家数据
首先,我们需要有一定量的专家数据,为此,预先通过PPO算法训练出一个表现良好的专家模型,再利用专家模型生成专家数据。本次代码实践的环境是CartPole-V0,以下是PPO代码内容。
import gym
import torch
import torch.nn.functional as F
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
import random
import rl_utils
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return F.softmax(self.fc2(x), dim=1)
class ValueNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim):
super(ValueNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
return self.fc2(x)
class PPO:
''' PPO算法,采用截断方式 '''
def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr,
lmbda, epochs, eps, gamma, device):
self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
self.critic = ValueNet(state_dim, hidden_dim).to(device)
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(),
lr=actor_lr)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(),
lr=critic_lr)
self.gamma = gamma
self.lmbda = lmbda
self.epochs = epochs # 一条序列的数据用于训练轮数
self.eps = eps # PPO中截断范围的参数
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.actor(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample()
return action.item()
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
self.device)
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'],
dtype=torch.float).view(-1, 1).to(self.device)
td_target = rewards + self.gamma * self.critic(next_states) * (1 -
dones)
td_delta = td_target - self.critic(states)
advantage = rl_utils.compute_advantage(self.gamma, self.lmbda,
td_delta.cpu()).to(self.device)
old_log_probs = torch.log(self.actor(states).gather(1,
actions)).detach()
for _ in range(self.epochs):
log_probs = torch.log(self.actor(states).gather(1, actions))
ratio = torch.exp(log_probs - old_log_probs)
surr1 = ratio * advantage
surr2 = torch.clamp(ratio, 1 - self.eps,
1 + self.eps) * advantage # 截断
actor_loss = torch.mean(-torch.min(surr1, surr2)) # PPO损失函数
critic_loss = torch.mean(
F.mse_loss(self.critic(states), td_target.detach()))
self.actor_optimizer.zero_grad()
self.critic_optimizer.zero_grad()
actor_loss.backward()
critic_loss.backward()
self.actor_optimizer.step()
self.critic_optimizer.step()
actor_lr = 1e-3
critic_lr = 1e-2
num_episodes = 250
hidden_dim = 128
gamma = 0.98
lmbda = 0.95
epochs = 10
eps = 0.2
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
"cpu")
env_name = 'CartPole-v0'
env = gym.make(env_name)
env.seed(0)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
ppo_agent = PPO(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, lmbda,
epochs, eps, gamma, device)
return_list = rl_utils.train_on_policy_agent(env, ppo_agent, num_episodes)
接下来开始生成专家数据,因为车杆环境比较简单,我们只生成了一条轨迹,并且从中采样30个状态动作对样本 ( s , a ) (s,a) (s,a)。我们只用这三十个专家数据样本来训练模仿策略。
def sample_expert_data(n_episode): # PPO算法生成的数据为专家数据
states = []
actions = []
for episode in range(n_episode):
state = env.reset()
done = False
while not done:
action = ppo_agent.take_action(state)
states.append(state)
actions.append(action)
next_state, reward, done, _ = env.step(action)
state = next_state
return np.array(states), np.array(actions)
env.seed(0)
torch.manual_seed(0)
random.seed(0)
n_episode = 1
expert_s, expert_a = sample_expert_data(n_episode)
n_samples = 30 # 采样30个数据
random_index = random.sample(range(expert_s.shape[0]), n_samples)
expert_s = expert_s[random_index]
expert_a = expert_a[random_index]
生成的专家数据(s,a) 前面是状态 后面是对应的动作
(s,a) [[ 1.54347057e-01 -3.43056279e-01 -7.70492116e-02 5.51903570e-01]
[ 1.40483075e-01 5.10391136e-02 -8.70243223e-02 -1.20774844e-01]
[ 8.53656083e-02 -5.33215846e-01 2.11255998e-02 7.33306250e-01]
[-2.37716142e-02 4.42306990e-02 -3.58161693e-03 2.99248916e-02]
[-6.42688771e-02 4.07792185e-02 9.05907638e-02 1.06461104e-01]
[ 1.30428031e-01 4.32922922e-01 -2.90091407e-02 -5.21424615e-01]
[ 7.44860918e-02 4.47529654e-02 4.13841868e-02 1.83654516e-02]
[ 1.28033513e-01 -5.33910287e-01 -3.77957219e-02 7.49323969e-01]
[ 3.33001522e-02 2.28139000e-01 4.63557199e-03 -1.54802321e-02]
[ 7.65677327e-02 4.57650880e-02 3.54701770e-02 -3.97965965e-03]
[ 1.32793656e-01 2.34499986e-01 -6.32762748e-02 -1.56095334e-01]
[ 1.21362307e-01 2.47391438e-01 -8.50646364e-03 -4.40147026e-01]
[-4.36434478e-02 -5.31503951e-01 5.61687891e-02 6.96368974e-01]
[ 1.17870690e-01 6.27867066e-01 -1.28081134e-02 -8.10051364e-01]
[ 1.43620682e-02 2.39895483e-01 -2.10476261e-02 -2.74778330e-01]
[-9.04775722e-03 8.14272876e-01 3.59555507e-02 -9.11410591e-01]
[ 9.68223893e-02 2.40729952e-01 -2.69143913e-02 -2.93312025e-01]
[-7.28989279e-03 4.55692369e-02 -5.34946634e-03 3.97161250e-04]
[ 1.34915664e-01 -3.33830500e-01 -4.62595955e-02 3.46929473e-01]
[-6.20700550e-02 4.31279078e-02 8.20664935e-02 5.44040639e-02]
[ 1.55225861e-01 4.63181913e-02 -5.42231122e-02 -1.62086725e-02]
[ 1.38340755e-01 5.38084587e-02 -4.17946127e-02 -1.81554343e-01]
[ 2.78662042e-02 2.40571359e-01 -3.80236866e-02 -2.89820441e-01]
[ 4.63268155e-02 6.18254207e-01 -1.80797233e-03 -5.98012477e-01]
[-6.37850805e-03 -1.49475588e-01 -5.34152311e-03 2.91387477e-01]
[-8.83664588e-03 4.50975376e-02 -1.16732780e-02 1.08033569e-02]
[ 9.25768483e-02 4.24631370e-01 -3.89568339e-02 -3.38608191e-01]
[ 8.64215859e-02 -3.43774621e-01 1.85695112e-02 5.65904325e-01]
[ 1.42492914e-01 -1.44510647e-01 -3.36920013e-02 1.81913908e-01]
[ 2.12581314e-02 2.44272827e-01 7.50505314e-02 -3.72528169e-01]] [1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1]
Process finished with exit code 0
这里用的是PPO算法,用别的算法也可以,或者就不用强化学习算法生成的专家数据也是完全可以的,目的就是为了寻找专家数据。
15.4.2 行为克隆的代码实践
在BC中,我们将专家数据中的 ( s t , a t ) (s_t,a_t) (st,at)中的 a t a_t at视为标签,BC则转化成监督学习中经典的分类问题,采用最大似然估计的训练方法可得到分类结果。
class BehaviorClone:
def __init__(self, state_dim, hidden_dim, action_dim, lr):
self.policy = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
self.optimizer = torch.optim.Adam(self.policy.parameters(), lr=lr)
def learn(self, states, actions): # 输入的状态和动作是专家数据 行为克隆学习这一部分
states = torch.tensor(states, dtype=torch.float).to(device)
actions = torch.LongTensor(actions).view(-1, 1).to(device)
print(torch.tensor(actions))
log_probs = torch.log(self.policy(states).gather(1, actions))
bc_loss = torch.mean(-log_probs) # 最大似然估计 输出的是每一行的平均值
self.optimizer.zero_grad() # 对策略进行更新
bc_loss.backward()
self.optimizer.step()
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(device)
probs = self.policy(state) # 已经优化过的策略
action_dist = torch.distributions.Categorical(probs) # 将传入的值做归一化处理
action = action_dist.sample() # 随机选择一个动作
return action.item()
def test_agent(agent, env, n_episode):
return_list = []
for episode in range(n_episode):
episode_return = 0
state = env.reset()
done = False
while not done:
action = agent.take_action(state)
next_state, reward, done, _ = env.step(action)
state = next_state
episode_return += reward
return_list.append(episode_return)
return np.mean(return_list)
env.seed(0)
torch.manual_seed(0)
np.random.seed(0)
lr = 1e-3
bc_agent = BehaviorClone(state_dim, hidden_dim, action_dim, lr)
n_iterations = 1000
batch_size = 64
test_returns = []
with tqdm(total=n_iterations, desc="进度条") as pbar:
for i in range(n_iterations):
sample_indices = np.random.randint(low=0,
high=expert_s.shape[0],
size=batch_size)
print(torch.tensor(expert_a[sample_indices]))
bc_agent.learn(expert_s[sample_indices], expert_a[sample_indices])
current_return = test_agent(bc_agent, env, 5)
test_returns.append(current_return)
if (i + 1) % 10 == 0:
pbar.set_postfix({'return': '%.3f' % np.mean(test_returns[-10:])})
pbar.update(1)
iteration_list = list(range(len(test_returns)))
plt.plot(iteration_list, test_returns)
plt.xlabel('Iterations')
plt.ylabel('Returns')
plt.title('BC on {}'.format(env_name))
plt.show()
报错信息:原网站上的代码有一点问题,报错一下信息
Traceback (most recent call last):
File "", line 201, in <module>
bc_agent.learn(expert_s[sample_indices], expert_a[sample_indices])
File "", line 155, in learn
log_probs = torch.log(self.policy(states).gather(1, actions))
RuntimeError: gather(): Expected dtype int64 for index
经过不断查资料,发现gather只能索引int64类型的数据,所以将原来的actions = torch.tensor(actions).view(-1, 1).to(device)即actions的类型转换为int64 经过输出发现原来的actions为int32类型的
当出现RuntimeError这个错误信息的时候大概率是因为索引类型不对,追根溯源找到应该的索引类型,再找到错误源进行更改即可
进度条: 100%|██████████| 1000/1000 [03:05<00:00, 5.40it/s, return=199.320]
实验结果表明BC无法学习到最优策略(不同设备运行结果可能会有不同),这主要是因为在数据量比较少的情况下,学习容易发生过拟合。
15.4.3 生成式对抗模仿学习的代码实践
首先实现判别器模型,其模型架构为一个两层的全连接网络,模型输入为一个状态动作对,输出一个概率标量。
class Discriminator(nn.Module): # 判别器模型
def __init__(self, state_dim, hidden_dim, action_dim):
super(Discriminator, self).__init__()
self.fc1 = torch.nn.Linear(state_dim + action_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, 1)
def forward(self, x, a):
cat = torch.cat([x, a], dim=1)
x = F.relu(self.fc1(cat))
return torch.sigmoid(self.fc2(x))
接下来正式实现GAIL的代码。每一轮迭代中,GAIL中的策略和环境交互,采样新的状态动作对。基于专家数据和策略新采样的数据,首先训练判别器,然后将判别器的输出转换为策略的奖励信号,指导策略用PPO算法做训练。
class GAIL:
def __init__(self, agent, state_dim, action_dim, hidden_dim, lr_d):
self.discriminator = Discriminator(state_dim, hidden_dim, action_dim).to(device) # 判别器模型
self.discriminator_optimizer = torch.optim.Adam(self.discriminator.parameters(), lr=lr_d)
self.agent = agent
def learn(self, expert_s, expert_a, agent_s, agent_a, next_s, dones): # 专家数据和采样得到的数据
expert_states = torch.tensor(expert_s, dtype=torch.float).to(device)
expert_actions = torch.tensor(expert_a).to(device)
agent_states = torch.tensor(agent_s, dtype=torch.float).to(device)
agent_actions = torch.tensor(agent_a).to(device)
expert_actions = F.one_hot(expert_actions.to(torch.int64), num_classes=2).float() # 将专家数据的动作进行独热编码
agent_actions = F.one_hot(agent_actions.to(torch.int64), num_classes=2).float()
expert_prob = self.discriminator(expert_states, expert_actions)
agent_prob = self.discriminator(agent_states, agent_actions)
# BCELoss是二分类的交叉熵损失函数
discriminator_loss = nn.BCELoss()(agent_prob,
torch.ones_like(agent_prob)) + nn.BCELoss()(expert_prob, torch.zeros_like(expert_prob))
self.discriminator_optimizer.zero_grad()
discriminator_loss.backward() # 根据交叉熵损失函数将GAIL判别器参数进行更新
self.discriminator_optimizer.step()
rewards = -torch.log(agent_prob).detach().cpu().numpy()
transition_dict = {
'states': agent_s,
'actions': agent_a,
'rewards': rewards, # 奖励不再是根据环境得到而是根据专家数据的判别器输出得到
'next_states': next_s,
'dones': dones
}
self.agent.update(transition_dict)
env.seed(0)
torch.manual_seed(0)
lr_d = 1e-3
agent = PPO(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, lmbda,
epochs, eps, gamma, device)
gail = GAIL(agent, state_dim, action_dim, hidden_dim, lr_d)
n_episode = 500
return_list = []
with tqdm(total=n_episode, desc="进度条") as pbar:
for i in range(n_episode):
episode_return = 0
state = env.reset()
done = False
state_list = []
action_list = []
next_state_list = []
done_list = []
while not done:
action = agent.take_action(state)
next_state, reward, done, _ = env.step(action)
state_list.append(state)
action_list.append(action)
next_state_list.append(next_state)
done_list.append(done)
state = next_state
episode_return += reward
return_list.append(episode_return)
gail.learn(expert_s, expert_a, state_list, action_list,
next_state_list, done_list)
if (i + 1) % 10 == 0:
pbar.set_postfix({'return': '%.3f' % np.mean(return_list[-10:])})
pbar.update(1)
iteration_list = list(range(len(return_list)))
plt.plot(iteration_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
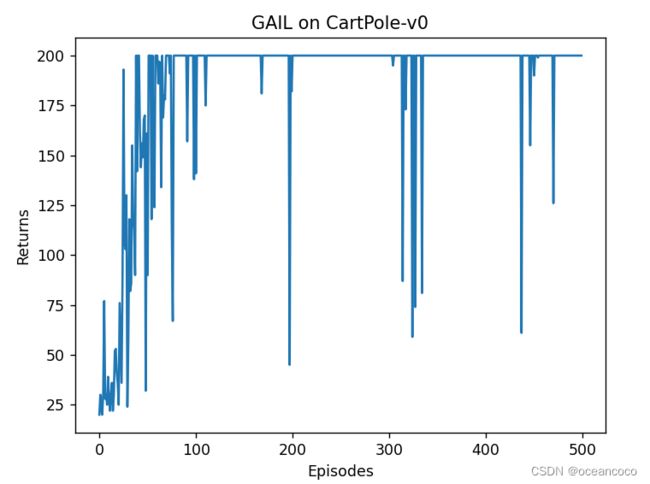
plt.title('GAIL on {}'.format(env_name))
plt.show()
生成对抗式网络是构造一个判别器模型,将智能体的状态动作和专家数据的状态动作进行交叉熵损失拟合,并且将结果用于作为状态动作的奖励,奖励就不再使用环境得到的奖励了,而是根据专家数据的判别器得到
进度条: 100%|██████████| 500/500 [00:35<00:00, 14.20it/s, return=200.000]
python
nn.BCELoss()
交叉熵损失函数
交叉熵主要是用来判定实际的输出与期望的输出的接近程度。在做分类训练的时候,如果一个样本属于第K类,那么这个类别所对应的输出节点的输出值应该为1,而其他节点的输出为0,即[0,0,0,1,0……,0,0],这个数组也就是样本的Lable,是神经网络最期望的输出结果。也就是说用它来衡量网络的输出与标签的差异,利用这种差异经过反向传播去更新网络参数。
在多分类问题中输出层的函数是Softmax函数,在二分类问题中的输出层的函数时Sigmod函数。
CrossEntropy损失函数适用于总共有N个类别的分类。当N=2时,即二分类任务,只需要判断是还是否的问题,就可以使用二分类交叉损失函数BCELoss
交叉熵原理
**信息量:**用来衡量一个事件的不确定性;一个事件发生的概率越大,不确定性越小,则它所携带的信息量就越小。假设X是一个离散型随机变量,其取值集合为X,概率分布函数为 p ( x ) = P ( X = x ) , x ∈ X p(x)=P(X=x),x\in X p(x)=P(X=x),x∈X,我们定义事件 X = x 0 X=x_0 X=x0的信息量为: I ( x 0 ) = − l o g ( p ( x 0 ) ) I(x_0)=-log(p(x_0)) I(x0)=−log(p(x0))当 p ( x 0 ) = 1 p(x_0)=1 p(x0)=1时,信息量将等于0,也就是说该事件的发生不会导致任何信息量的增加。
**熵:**用来衡量一个系统的混乱程度,代表一个系统中信息量的总和;信息量总和越大,表明这个系统不确定性就越大。
**交叉熵:**它主要刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。假设概率分布p为期望输出,概率分布q为实际输出,H(p,q)为交叉熵,则
H ( p , q ) = − Σ x ( p ( x ) l o g q ( x ) ) + ( 1 − p ( x ) ) l o g ( 1 − q ( x ) ) ) H(p,q)=-\varSigma _x(p(x)logq(x))+(1-p(x))log(1-q(x))) H(p,q)=−Σx(p(x)logq(x))+(1−p(x))log(1−q(x)))
当实际输出概率和期望概率差不多时,交叉熵会小
pytorch交叉熵实现
交叉熵损失是分类中最常用的一个损失函数。在Pytorch中是基于下面的公式实现的。
L o s s ( x ^ , x ) = Σ n i = 1 x log ( x ^ ) Loss\left( \widehat{x},x \right) =\underset{i=1}{\overset{n}{\varSigma}}x\log \left( \widehat{x} \right) Loss(x ,x)=i=1Σnxlog(x )
其中 x x x是真实标签, x ^ \widehat x x 是预测的类分布(通常是使用softmax将模型输出转换为概率分布)
BCELoss
L o s s = − 1 N Σ n i = 1 [ y i l o g ( p i ) + ( 1 − y i ) l o g ( 1 − p i ) ] Loss=-\frac{1}{N}\underset{i=1}{\overset{n}{\varSigma}}[y_i log(p_i)+(1-y_i)log(1-p_i)] Loss=−N1i=1Σn[yilog(pi)+(1−yi)log(1−pi)]
crossentropyloss
H ( p , q ) = − Σ x ( p ( x ) l o g q ( x ) ) + ( 1 − p ( x ) ) l o g ( 1 − q ( x ) ) ) H(p,q)=-\varSigma _x(p(x)logq(x))+(1-p(x))log(1-q(x))) H(p,q)=−Σx(p(x)logq(x))+(1−p(x))log(1−q(x)))
L o s s ( x ^ , x ) = Σ n i = 1 x log ( x ^ ) Loss\left( \widehat{x},x \right) =\underset{i=1}{\overset{n}{\varSigma}}x\log \left( \widehat{x} \right) Loss(x ,x)=i=1Σnxlog(x )
crossentropyloss()和BCELoss()原理是一样的,但是具体的计算结果是不一样的,首先是公式就不一样
import torch
import torch.nn as nn
from math import log
bce_loss = nn.BCELoss()
pred_pro = torch.tensor([0.8, 0.2, 0.4], dtype=torch.float)
label = torch.tensor([1, 0, 0], dtype=torch.float)
print(bce_loss(pred_pro, label))
cro = nn.CrossEntropyLoss()
print(cro(pred_pro, label))
tensor(0.3190)
tensor(0.7971)
实验证明两个结果是不一样的,但是经过计算发现不止是公式不同,本人知识有限,没有再深究了 欢迎各位补充
大概知道什么意思能能用就行
right)$$
crossentropyloss()和BCELoss()原理是一样的,但是具体的计算结果是不一样的,首先是公式就不一样
import torch
import torch.nn as nn
from math import log
bce_loss = nn.BCELoss()
pred_pro = torch.tensor([0.8, 0.2, 0.4], dtype=torch.float)
label = torch.tensor([1, 0, 0], dtype=torch.float)
print(bce_loss(pred_pro, label))
cro = nn.CrossEntropyLoss()
print(cro(pred_pro, label))
tensor(0.3190)
tensor(0.7971)
实验证明两个结果是不一样的,但是经过计算发现不止是公式不同,本人知识有限,没有再深究了 欢迎各位补充
大概知道什么意思能能用就行