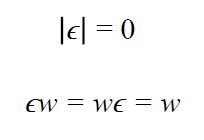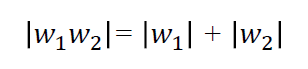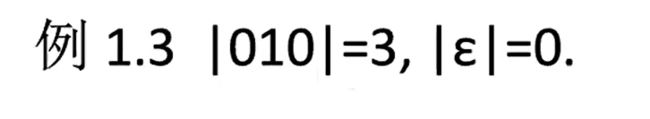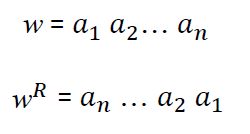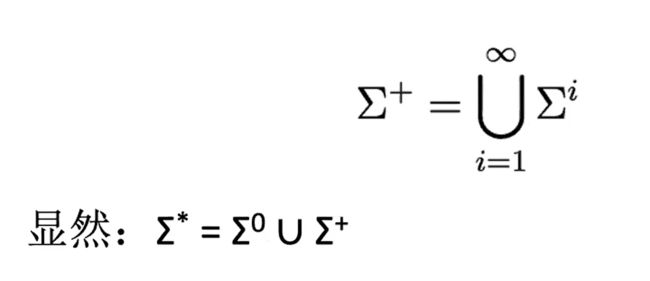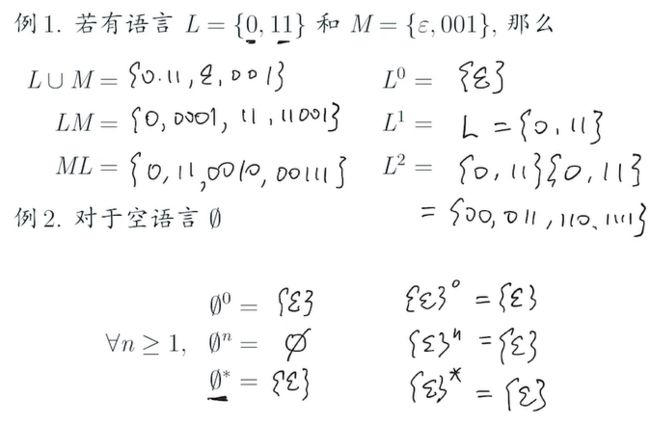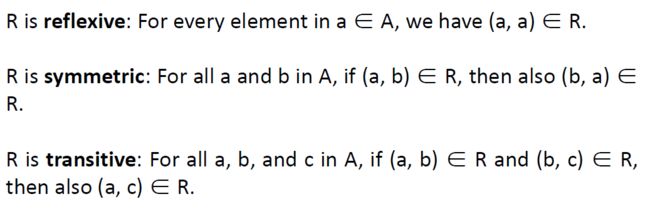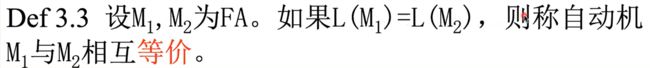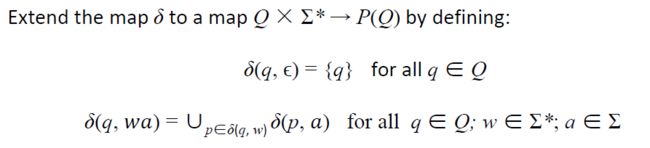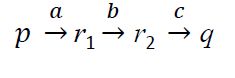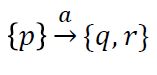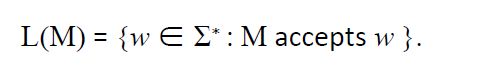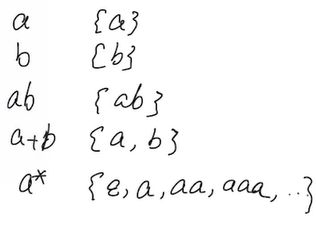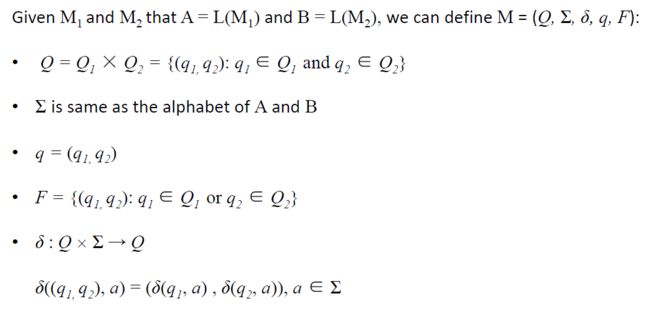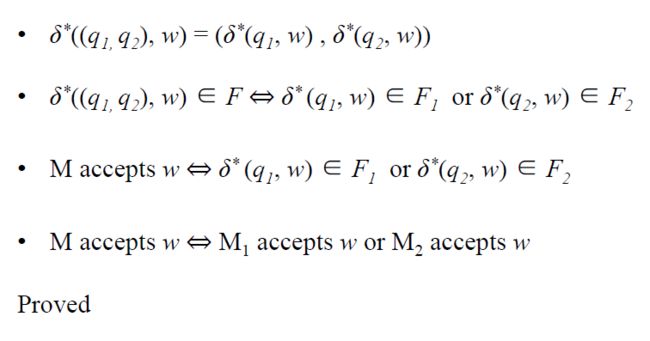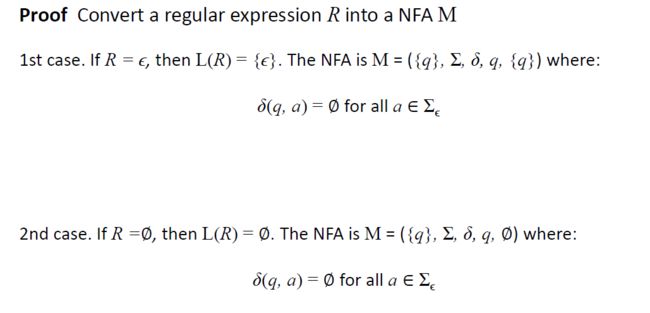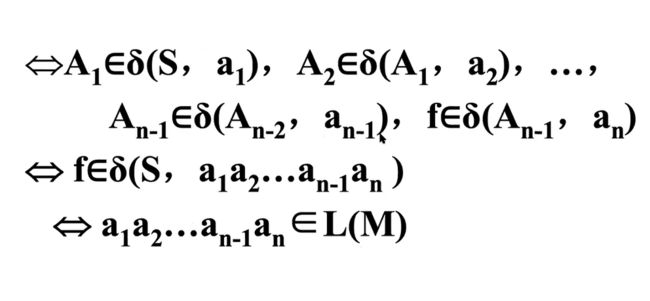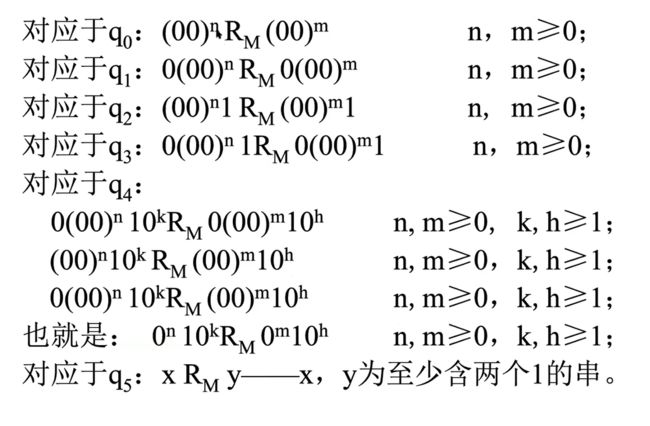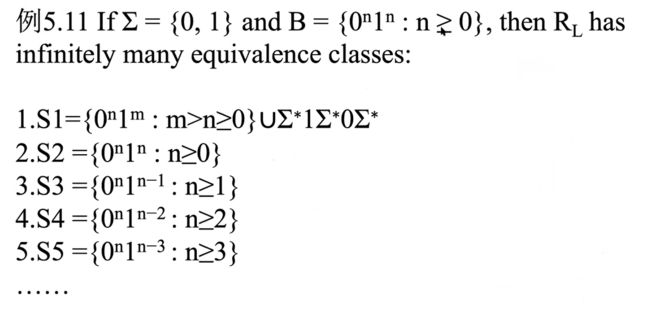INT201 形式语言与自动机笔记(上)
Lec1 Overview
Alphabet and String 字母表与字符串
Alphabet(字母表) a finite, nonempty set ∑ of symbols.
String (word) – a finite sequence of symbols from the alphabet
e.g
∑ = {a, b}, then abab, aaaabbba are strings on ∑
ε Empty string (word) 空字符串
the string with no symbols, denoted as ε
|w| length of a string 字符串长度
字符串中符号的数目 |w|
w reverse of a string 字符串反转
通过逆序书写符号得到 w
回文(palindrome)是一个字符串w满足 w =wR
concatenation 字符串连接
是通过将符号附加到右端来获得的(连接是关联的).
如果u, v, w是字符串,且w=uv,则u是w的前缀(prefix),v是w的后缀(suffix)。w的适当前缀是不等于w的前缀(类似于适当后缀)。
Wn是表示w的n个拷贝的连接
字母表的幂
如果∑是一个字母表,则用指数记号来表示这个字母表某个长度的所有串的集合。即∑^k 是长度为k的串的集合,这些串的每个符号都属∑。
任何集合的0次幂都是集合本身
closure 闭包
∑* star closure of∑ 表示∑上所有字符串(词)的集合。
∑+ positive closure of ∑ 表示∑上所有非空字符串(词)的集合。
∑* Kleene Closure 克林闭包
∑+ Positive Closore 正闭包
Language语言
alphabet ∑上的语言L(或形式语言formal language)是 ∑*的子集,语言就是字符串string的集合
我们可以使用连接和闭包来用其他语言来表达新的语言:
研究主要包括:
1.表示(representation)无穷语言的表示
2.有穷描述(finite description)
3.结构(structure)
表示方法:
1.L是有限集合
列举法
2.L无限集合
方法一:文法 产生系统:由定义的文法规则产生出语言的每个句子
方法二:机器识别系统:当一个字符串能被一个语言的识别系统接受,则这个字符串是改语言的一个句子,否则不属于该语言
语言的计算
Gramma 文法
生成语法正确的程序/句子的规则集。
Lexical Analysis 词法分析
将字符序列划分为标记,如变量名、操作符、标签等。在自然语言中,标记是由连续字母组成的字符串(很容易识别!)
Parse Tree 解析树
识别令牌token之间的关系
解析树或解析树或派生树或具体语法树是一种有序的、有根的树,它根据一些与上下文无关的语法表示字符串的语法结构。
定义
α→β是α产生β的意思
约定
e.g
推导(derives),句型(sentential form),句子(sentence),规约(reduce)
注意,句子是由终结符构成的的T*,句型是由终结符和变元构成的(VUT)*
?
文法产生的语言
文法等价
文法的乔姆斯基体系
|α|<|β|指的是alpha长度小于β长度
e.g
liner 线性文法&线性语言
Automata 自动机
自动机是数字计算机的抽象模型
可计算性理论(Computability Theory): 的中心问题:将问题分为可解的和不可解的。
自动机理论中心问题:这些模型是否具有相同的能力,或者一个模型可以比另一个模型解决更多的问题? 自动机理论处理不同类型的“计算模型”的定义和性质。
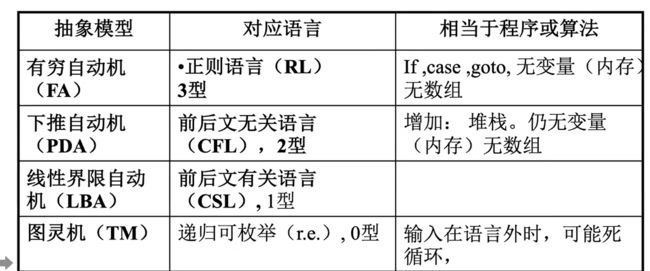
•有限自动机 Finite Automata。它们用于文本处理、编译器和硬件设计。
•上下文无关语法 Context-Free Grammars 。它们用于定义编程语言和人工智能。
•图灵机 Turing Machines。这些构成了一个简单的抽象模型,一个“真正的”计算机,如你在家里的个人电脑。
1. Finite Automata 有限状态自动机
Regular language 正则语言(RL)3型语言
2. Push down Automata 下推自动机
前后文无关语言 CFL 2型语言
3. Linear Bounded Automata 线性有界自动机
前后文有关语言 CSL 3型语言
4. Turing Machine
递归可枚举 0型语言
数学预备知识
这一块跟离散还是很像的!
Set 集合
集合是定义良好的对象的集合
如果A和B是集合,则A是B的一个子集,记为 A ⊆ B A的每个元素也是B的一个元素。
Relation and function
function
一个从A到B的函数f,记作f: A→B,是一个二元关系R,它具有这样的性质:对于每个元素A∈A,在R中存在一个有序对,其第一个分量是A。我们也可以说f(A) = B,或者f映射A到B,或者A在f下的像是B。集合A称为f的定义域,集合A称为f的定义域,然后集合{b ∈ B : there is an a ∈ A with f(a) = b}被称为f域
函数f: A→B是一对一的(或单射),如果对于A中的任意两个不同的元素A和A′,则有f(A)≠f(A′)。函数f是映上的(或满射),如果对于每个元素b∈b,存在一个元素a∈a,使得f(a) = b;换句话说,f的值域等于集合b,函数f是一个双射,如果f既是单射又是满射。
Binary relation
两个集合A和B上的二元关系是A × B的子集(A与B的笛卡尔积)。
等价 equivalence relation 满足
图 Graph
图G = (V, E)是由集合V和集合E组成的一对,集合V的元素称为顶点vertices,集合E的每个元素是一对不同的顶点。E中的元素叫做边edges。
顶点v的度数,用deg(v)表示,定义为与v相关的边的个数。
path 图中的路径 是由边连接的顶点序列。
circle 如果路径的起点和终点都在同一个顶点,那么它就是一个循环。
simple path 简单路径是没有任何重复顶点的路径。
connected 如果每个顶点对之间都有一条路径,那么这个图就是连通的。
证明
技术
Axiom, statement, theorem, proof
策略
直接证明 Direct
建设性证明 Constructive
非建设性证明 Non-Constructive
矛盾证明 Contradiction
归纳证明 Induction
Lec2 Deterministic Finite Automata(DFA) 确定性有穷自动机
有穷自动机
有穷自动机是一种有限状态机,它通过运行由字符串唯一确定的状态序列来接受或拒绝给定的符号字符串。
它的发明是为了识别一类特殊的形式语言
e.g Lexical analysis, Model checking
可以描述:
任意字符串的有限集合
各种字符串的无限集合 e.g 超过6个字母的字符串
不可描述:
1)包含a多于b的字符串集 2)如果你从头到尾读它们,所有的单词保持不变3)格式良好的算术表达式,如果没有嵌套括号的限制
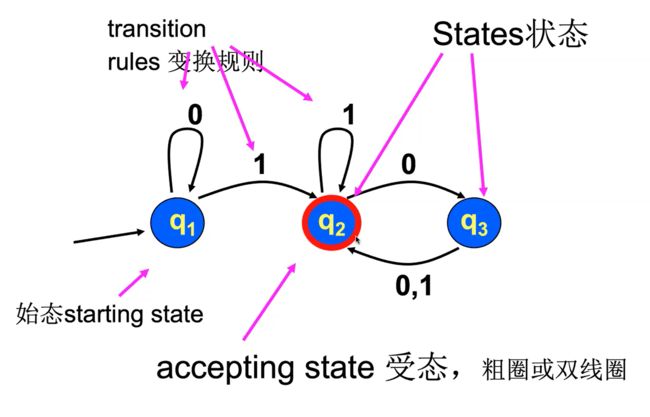
定义
M = (Q, Σ, δ, q, F)
-
Q 是有限状态集合(Finite Set of States): 这表示自动机中存在一个有限数量的不同状态。每个状态代表了自动机在某个特定时刻的内部状态。这些状态可以用符号或名称表示。
-
Σ 是有限符号集合(Finite Set of Symbols,即字母表): 这是自动机操作的输入符号的有穷的非空集合,通常称为自动机的字母表或输入字母表。它包含了自动机能够接受和处理的所有可能输入符号。(字符串:从某个字母表中选择的符号的有穷序列)
-
δ : Q × Σ → Q 是转移函数(Transition Function): 这个函数描述了自动机如何从一个状态通过某个输入符号转移到另一个状态。它接受一个当前状态和一个输入符号,然后返回下一个状态。这个函数是有限自动机的核心,它定义了状态转移规则。
-
q ∈ Q 是初始状态(Initial State): 这表示自动机在开始运行时处于的初始状态。初始状态是自动机的起点,从这里开始处理输入。
-
F ⊆ Q 是接受/终止状态集合(Set of Accepting/Terminal States): 这是自动机可能达到的状态的子集。当自动机在某个状态属于 F 时,它被认为已经接受了输入字符串。这些状态通常表示自动机在识别输入时的终止状态。
state
机器的状态告诉您有关目前已读取的前缀的一些信息。如果字符串是感兴趣的语言的成员,当整个字符串被扫描时达到的状态将是一个接受状态(F的成员)。
Transition function
转换函数δ告诉你当DFA读取一个额外的字母时状态应该如何变化。
我们可以扩展转换函数δ的定义,让它告诉我们在扫描一个单词(不仅仅是一个字母)后我们到达了哪个状态:
δ* 是在自动机理论中常用的符号,表示自动机的状态转移函数的闭包操作。具体来说,对于一个给定的自动机 M,δ* 表示状态转移函数 δ 的闭包,它表示从自动机的初始状态出发,可以经过零次或多次状态转移,达到一个或多个状态的集合。更具体地说,如果 q 是自动机 M 的一个状态,那么 δ*(q, w) 表示从状态 q 出发,通过状态转移函数 δ,可以接受一个输入字符串 w(可能为空串 ε),并最终到达的状态集合。
Transition Grapth
DFA M = (Q, Σ, δ, Q, F)通常被描述为一个有向图GM(称为过渡图)有|Q|个顶点,每个顶点标记为不同的qi∈Q。对于每个transition function δ(qi, A) = qj,图的边(qi, qj)标记为(a), (b)和(a, b),。与q1相关的顶点称为初始顶点initial vertex,而标记为qf的顶点称为最终顶点 final vertices。
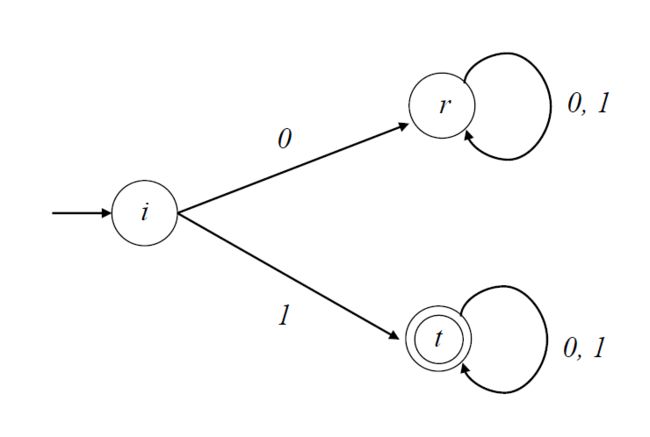
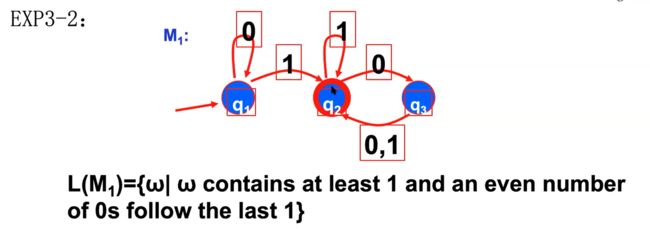
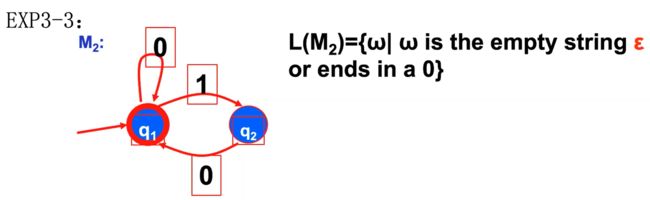
e.g1
e.g2
由DFA定义的语言
假设我们有一个DFA M,如果δ*(q0, w)∈F,就说单词w∈Σ*被M接受accept或识别recognized,否则就说它被拒绝rejected。M接受的所有单词的集合称为M接受的语言,用L(M)表示。因此
任何有限的语言都被某些DFA所接受
eg.1
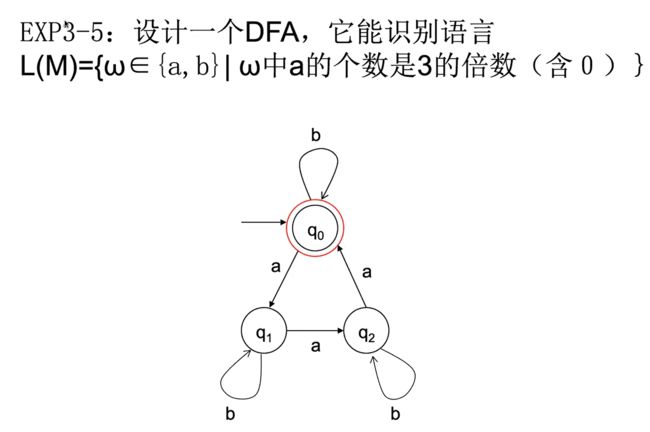
如何设计有穷自动机
e.g1
e.g2
正则语言regular
如果存在一个有限自动机M,使得A = L(M),则称为正则语言A。
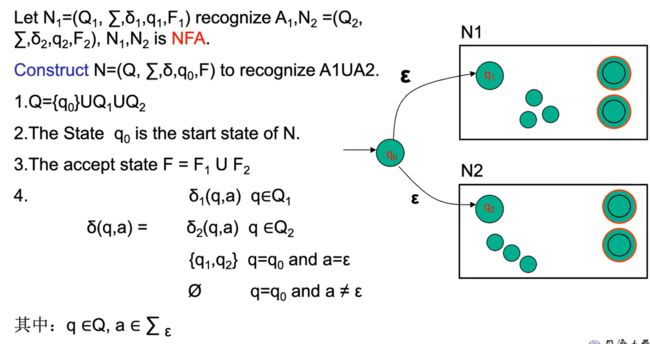
正则语言的集合在联合运算下是封闭的,即如果A和B是相同字母表Σ上的正则语言,那么A∪B也是正则语言。
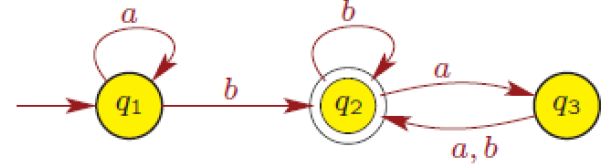
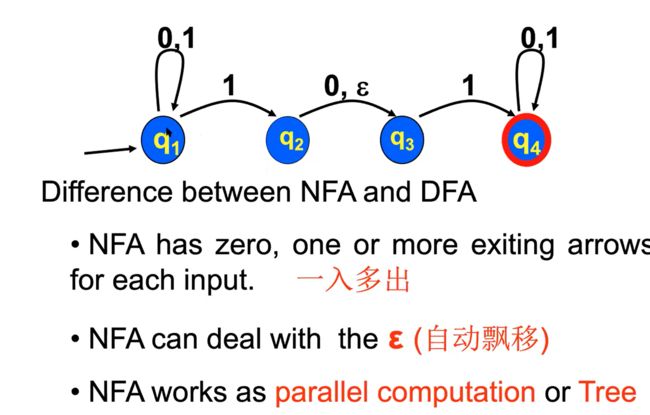
Lec3 Nondeterministic Finite Automata(NFA) 不确定的有穷自动机
有限自动机是确定性的deterministic,如果机器在任何给定符号上的下一个状态是唯一确定的。
DFA对每个符号只有一个离开每个状态的转换。
NFA处于具有多种继续方式的状态,例如状态q1有两条转换路径,路径为1。
e.g1
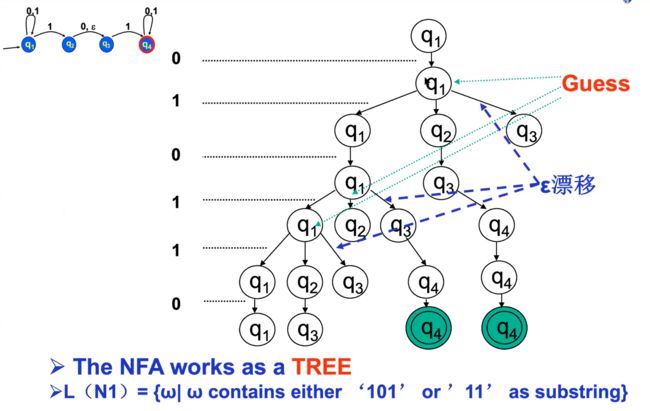
机器分裂成自身的多个副本(线程):
•每个副本都独立地进行计算。
•nfa可能处于一组状态,而不是单一状态。
•nfa遵循所有可能的并行计算路径。
•如果副本处于某种状态,并且下一个输入符号没有出现在该状态的任何输出边缘上,则副本死亡或崩溃。
定义
对于任意字母Σ,我们定义Σϵ为状态集合,而非一个状态
![]()
回想幂集的概念: 对于任意集合Q,幂集P(Q)是Q的所有子集的集合:
非确定性有限自动机(NFA)是一个5元组M = (Q, Σ, δ, Q, F),其中
1. Q是有限状态的集合。
2. Σ是一组有限的符号,称为自动机的字母表,
3。δ: Q × Σϵ→P(Q)是一个函数,称为过渡函数 其中 P(Q)是一个状态集合
4。q∈q称为初始/开始状态,
5。F: Q是一组接受状态/终结状态。
e.g1
e.g2
![]()
你看这里q1-1就是一个状态的集合
NFA和DFA对比
dfa具有过渡函数δ: Q ×Σ→Q
nfa具有过渡函数δ: Q ×Σϵ→P(Q)
nfa
返回一组状态而不是单个状态。
允许ϵ-transition,因为Σϵ = Σ∪{ϵ}。
每个DFA也是一个NFA。
因此,δ(q, w)是在状态q下接收输入w时可能出现的所有可能状态的集合,只要δ(q, w)包含一个接受状态,那么w是可以接受的。
* accepting/rejecting paths
假设,在DFA中,我们可以通过用单词w标记的转换从状态p到状态q。然后我们说状态p和q通过一个标签为w的路径连接。
如果w = abc两个中间态分别是r1和r2我们可以这样写
在NFA中,如果(p,a)= {q, r},我们可以这样写:
如果RHS上的任何状态都是可接受的状态,那么这就是一条可接受的路径,否则就是一条被拒绝的路径。
由NFA定义的语言
设M = (Q, Σ, δ, Q, F)为NFA。M所接受的语言L(M)定义为
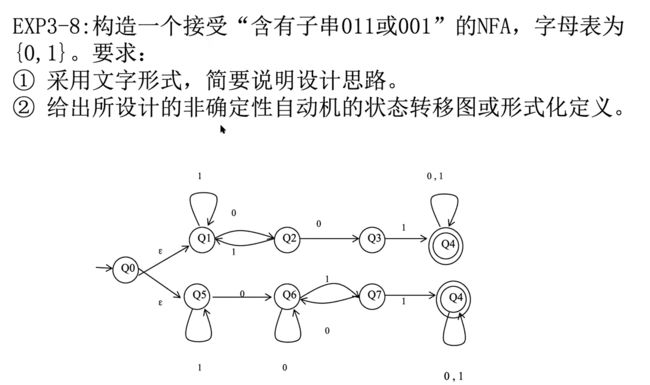
NFA自动机设计
?为什么不能一条线解决?
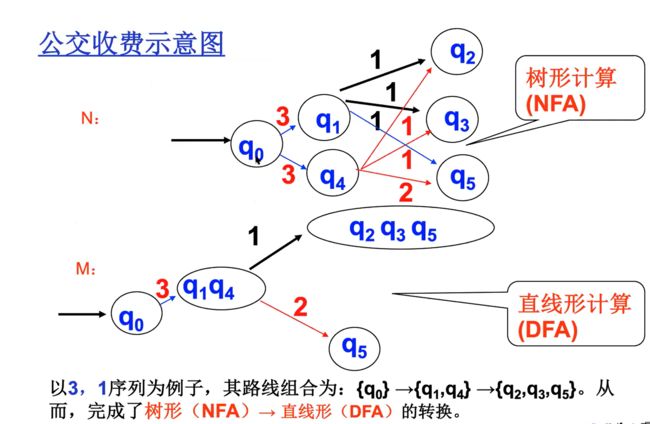
DFA和NFA等价
如果两台机器(任何类型)识别相同的语言,则它们是等效的。
DFA是NFA的一种限制形式:
•每个NFA都有一个等价的DFA。
•我们可以将任意的NFA转换为接受相同语言的DFA。
•dfa具有与NFA相同的权力
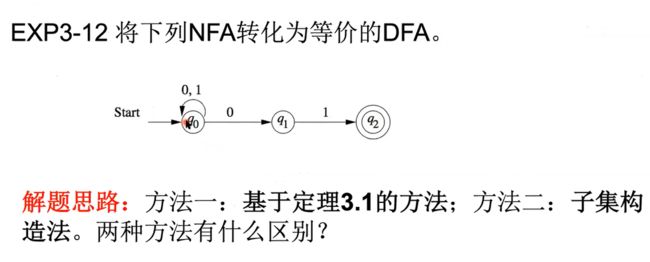
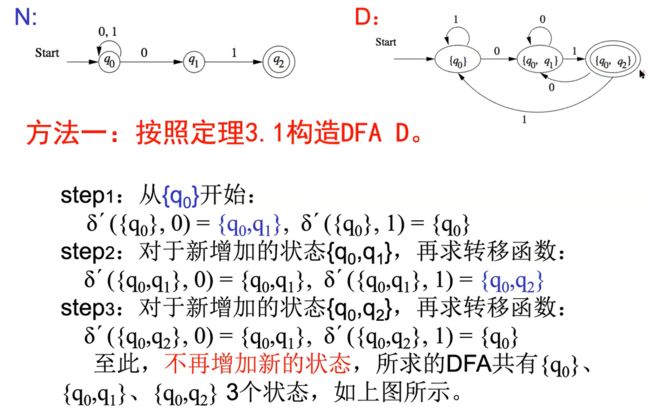
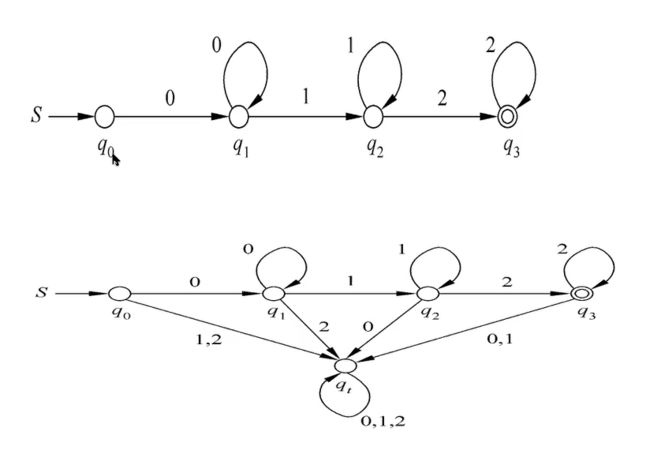
e.g1
e.g2
e.g3
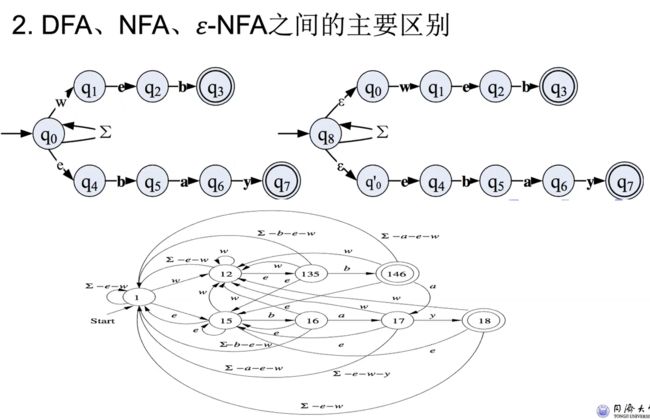
主要区别
e.g
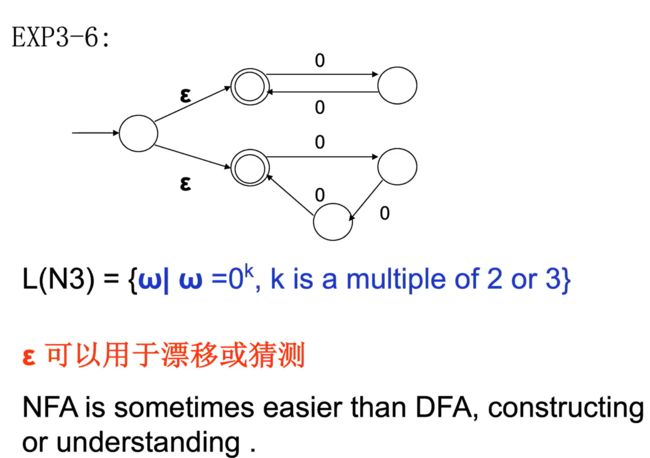
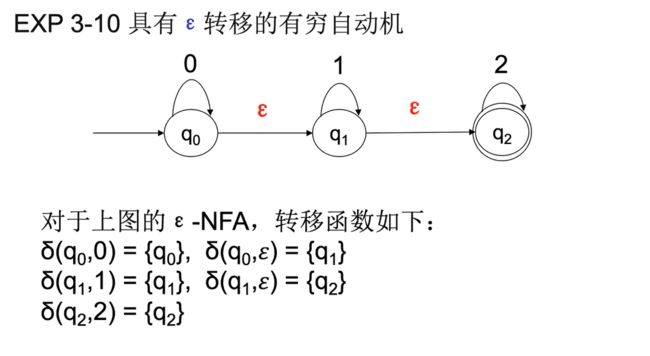
带空转移的有穷自动机 ε-NFA
e.g1
0步集*
这个不需要掌握吧?
扩充转移函数δ^*
这个不需要掌握吧?
文本搜索的NFA *
补充概念
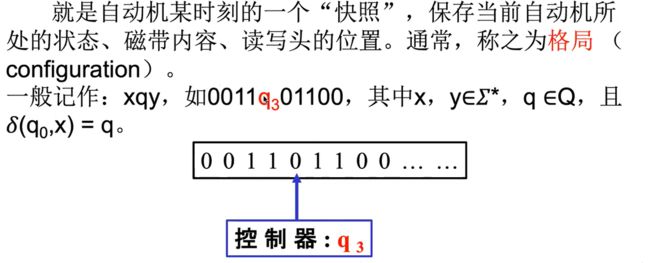
instrantaneous description ID 即时描述
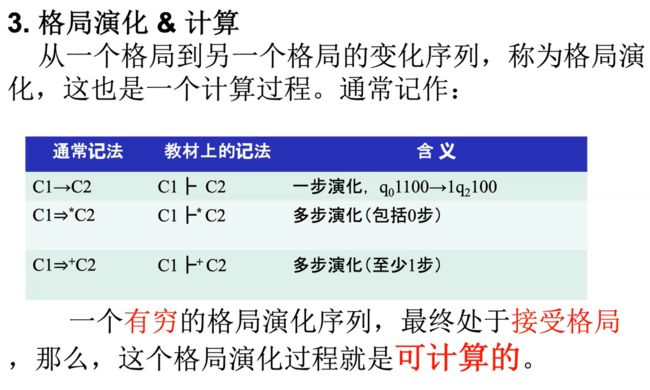
陷进状态
Lec4-5 Regular Language 正则语言
定义
以前:如果一种语言被某些DFA识别,那么它就是正则语言
现在:当且仅当某些NFA识别该语言时,该语言才是正则语言。
语言上的一些操作:Union, concatation和Kleene *
运算
e.g1
e.g2
Closed封闭性
如果对S中的成员应用f总是返回一个仍在S中的对象,则对象集合S在操作f下关闭。
常规语言在常规操作(例如联合、连接、星号)下确实是封闭的。
Under Union
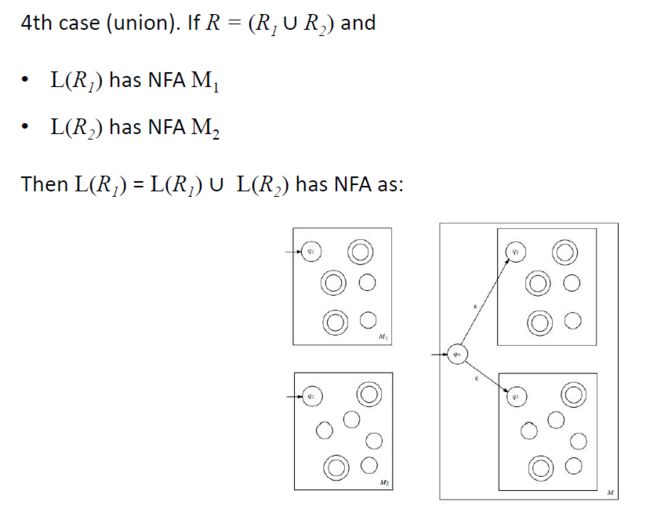
正则语言集在联合操作下是封闭的。
即A和B是相同字母表上的正则语言Σ,那么A∪B也是正则语言。
证明
1.
2.
3.
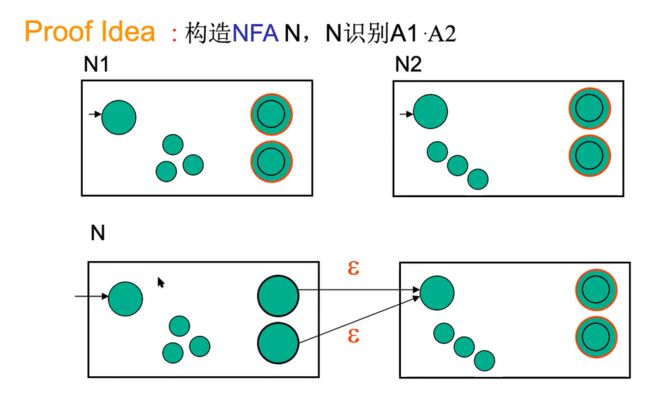
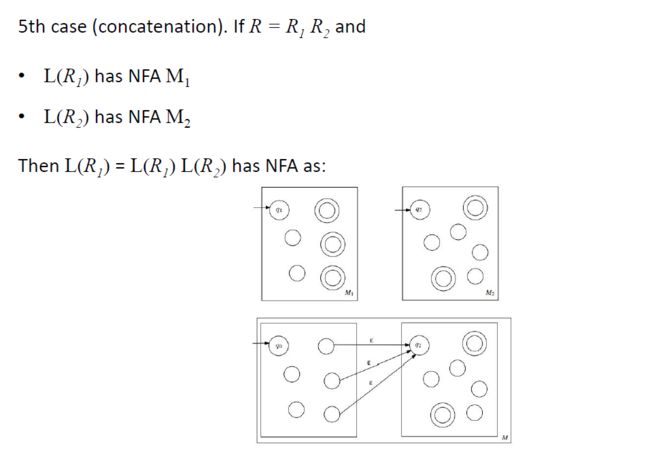
Under Concatenation
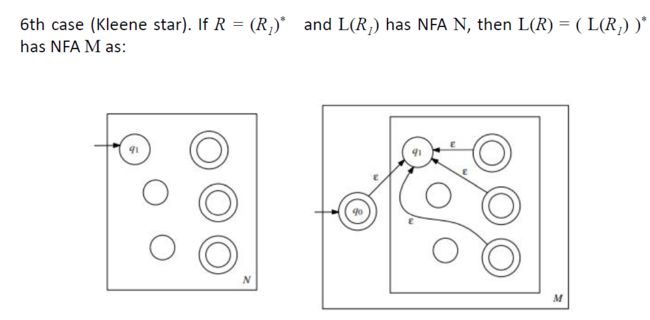
Under kleene star
Under Complement and Interaction
Regular Expression 正则表达式
正则表达式是描述某些语言的方法。
*运算就是把里面的东西不断重复
正式定义
让Σ为非空字母表
1. ϵ是正则表达式。
2. ∅是一个正则表达式。
3. 对于每个a∈Σ, a为正则表达式。
4. 若R1和R2为正则表达式,则R1∪R2为正则表达式。
5. 如果R1和R2是正则表达式,则R1 R2是正则表达式。
6. 如果R是正则表达式,则R *也是正则表达式。
如果R是正则表达式,则L(R)是由R生成(或描述或定义)的语言。
让Σ为非空字母表
1. 正则表达式ε描述了语言{ε}。
2. 正则表达式∅描述语言∅。
3. 对于每个a∈Σ,正则表达式a描述语言{a}。
4. 设R1和R2为正则表达式,L1和L2分别为它们所描述的语言。正则表达式R1∪R2描述了语言L1∪L2。
5. 设R1和R2为正则表达式,L1和L2分别为它们所描述的语言。正则表达式R1R2描述了语言L1L2。
6. 设R是一个正则表达式,L是它所描述的语言。正则表达式R *描述语言L *。
e.g 1
构造正则表达式
e.g1
e.g2
e.g3
e.g5
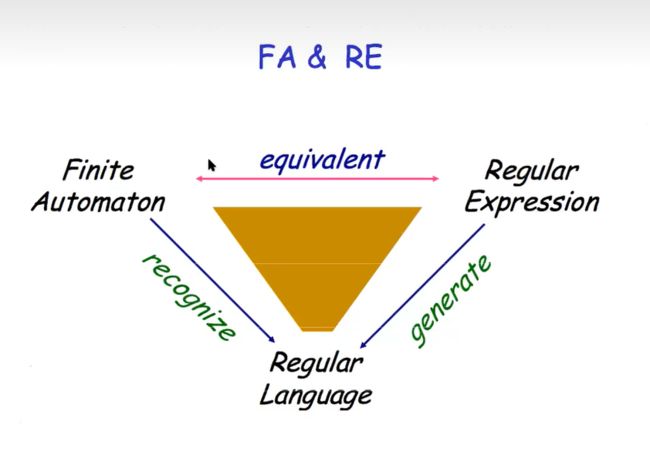
Kleene's Theorem 克林正则集定理
正则表达式与FA等价关系
1)如果一种语言是正则的,那么它有一个正则表达式
e.g1
e.g2
e.g3
2) 如果一种语言是用正则表达式描述的,那么它就是正则的。
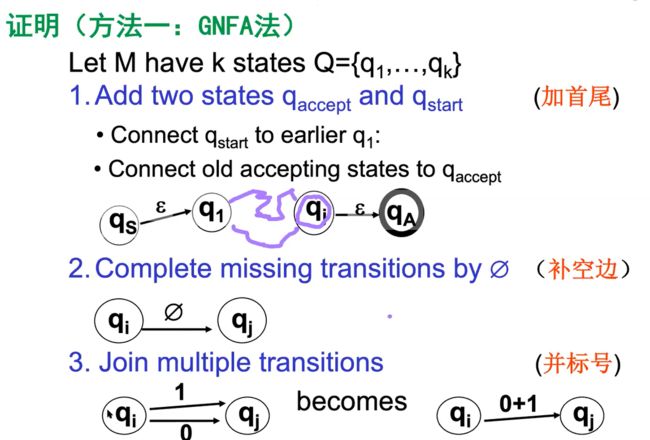
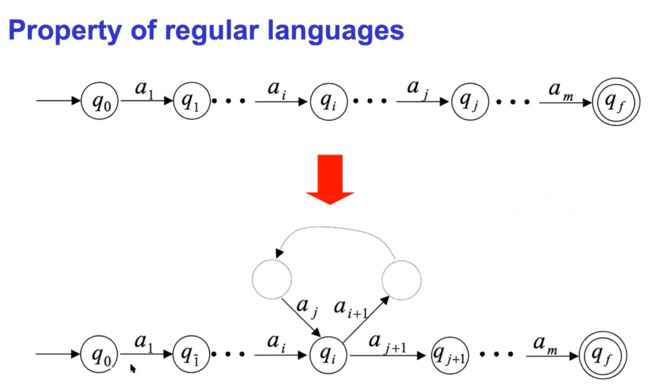
Generalized NFA (GNFA)
GNFA可以定义为一个5元组(Q, Σ, δ, {s}, {t})
•有限状态集Q;
•一个称为字母表Σ的有限集合;
•一个转换函数(δ:(Q∖{t})×(Q∖{s})→R);
•起始状态(s∈Q);
•接受状态(t∈Q);
其中R是字母表上所有正则表达式的集合Σ
特点
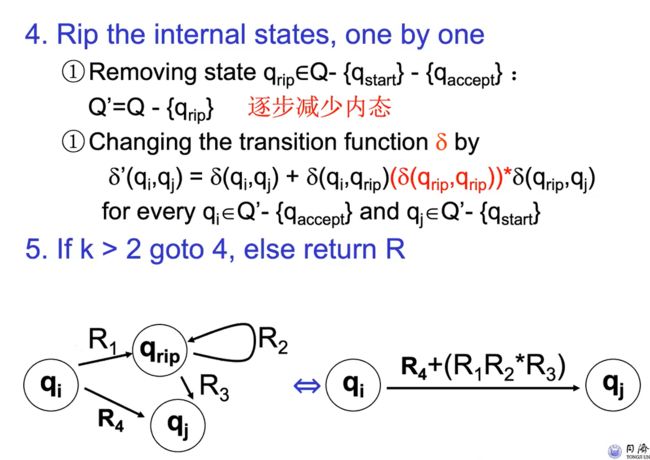
证明步骤
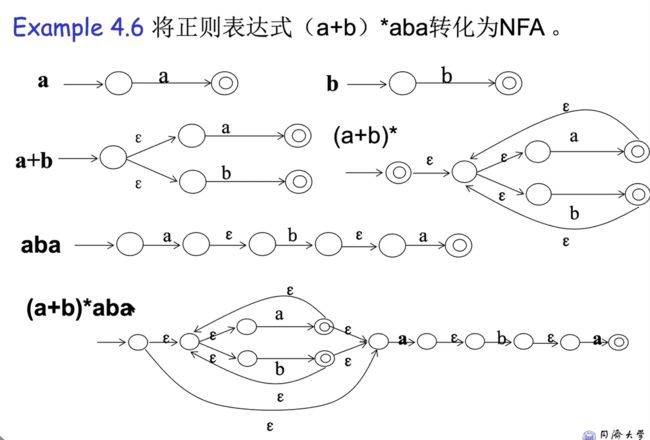
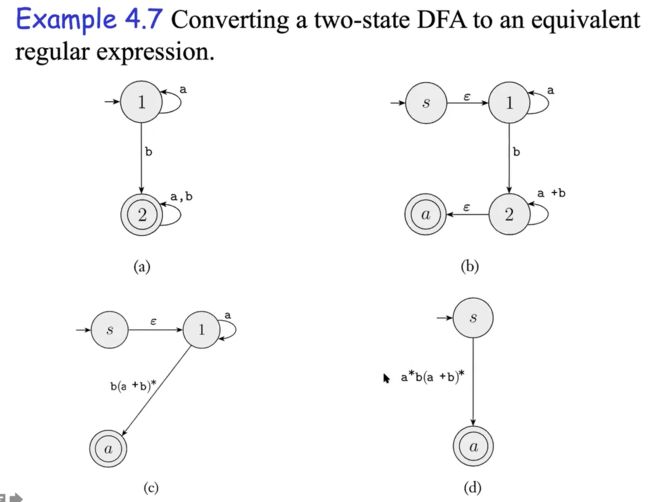
e.g1
删到两个状态后剩下的正则表达式就是我们所需要的
e.g1
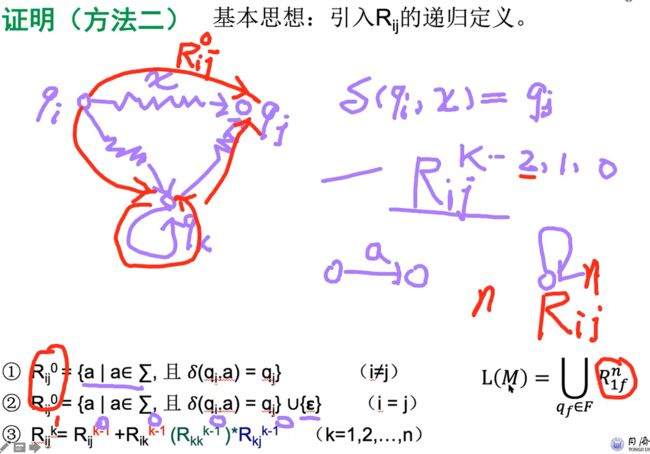
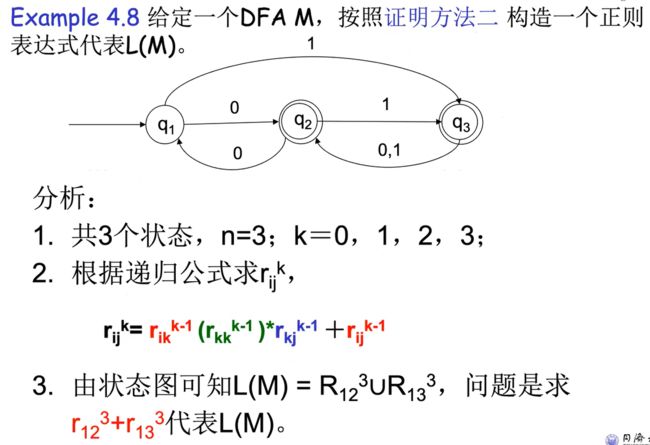
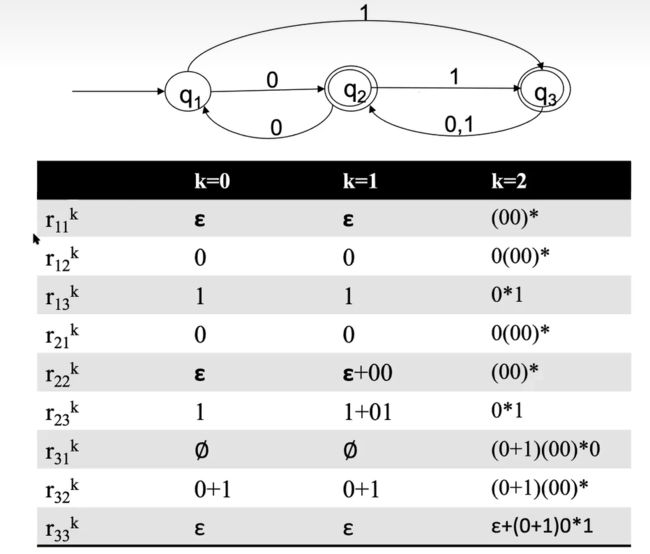
Rijk迭代法
将DFA M = (Q, Σ, δ, Q, F)转换为正则表达式的迭代过程
1. 将DFA M = (Q, Σ, δ, Q, F)转换为等效GFNA G:
•引入新的启动状态
•引入新的开始状态t
•将边缘标签更改为正则表达式,例如,“a, b”变为“a∪b”
2. 从GNFA G中迭代地消除一个状态,直到只剩下2个状态:开始start和接受accept
•需要考虑所有可能的先前路径。
•永远不要消除新的开始状态或新的接受状态
步骤
对不起我已经晕晕了
e.g1
q1到q2(R123,3式因为q1到q2可以经过任何状态,小于3就ok)U q1到q3
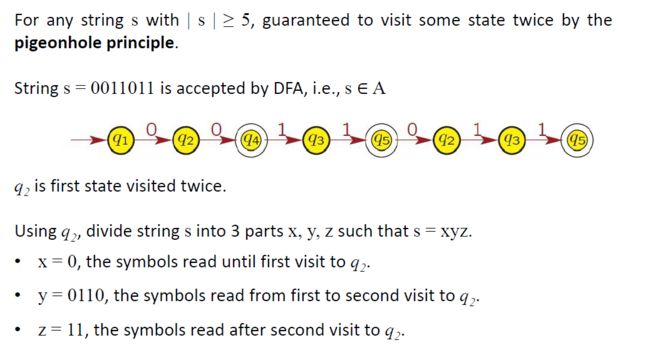
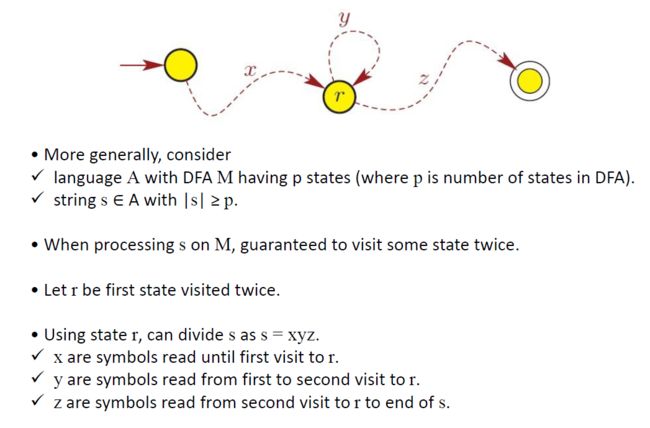
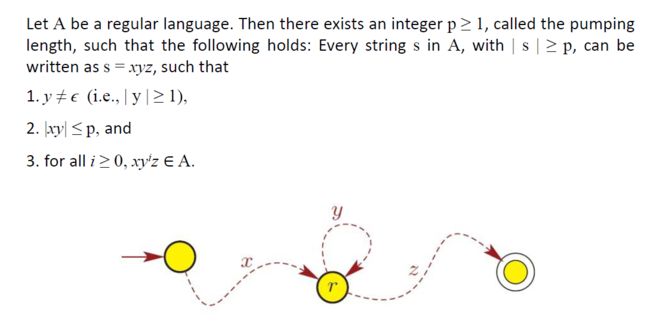
Pumping Lemma for Regular Languages 正则语言的泵引论
一种可以用来证明某些语言不正规的工具。这个定理说明所有的规则语言都有一个特殊的性质。
该属性指出,如果语言中的所有字符串至少与某个特殊值(称为抽运长度pumping length)一样长,则可以“抽运pumped”。
• 如果语言L是正则的,它总是满足抽运引理。如果存在至少一根由抽运而成的字符串不在L中,那么L肯定不是规则的。
• 相反的情况可能并不正确。如果抽运引理成立,并不意味着语言是规则的。
状态有重复
大于P的时候打圈
e.g1
e.g2
e.g3
有穷的,所以可以枚举
e.g4
e.g5
素数p0的(1+|y|)次方就不是素数了
e.g6
e.g7
e.g8
正则表达式的代数定律
![]()
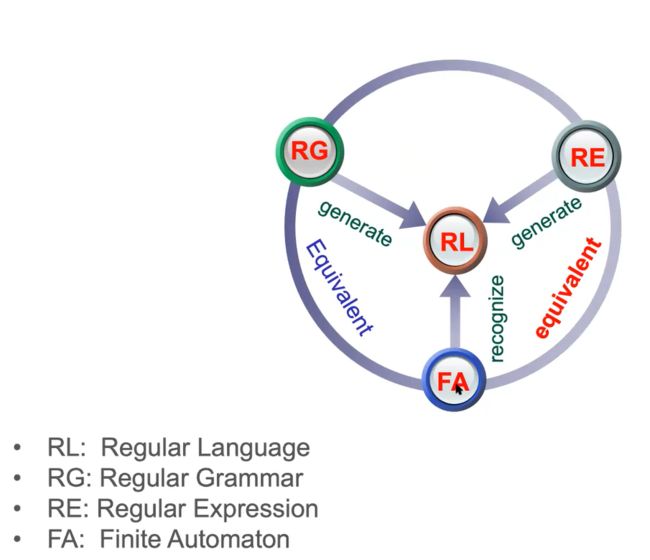
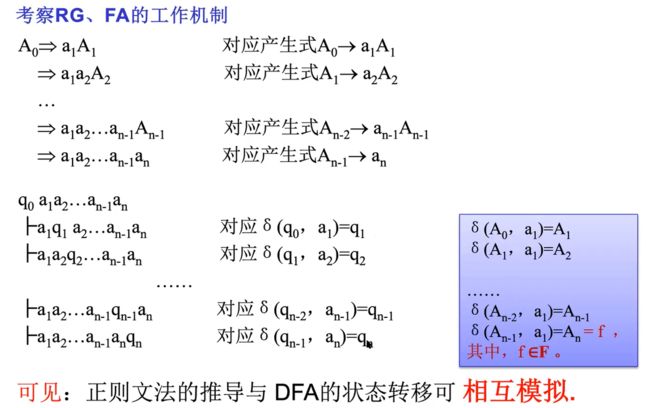
FA与RG的等价性
FA接受的语言是正则语言
L(G)是文法产生,L(M)是DFA产生
e.g1
正则语言可以由FA接受
e.g1
e.g2
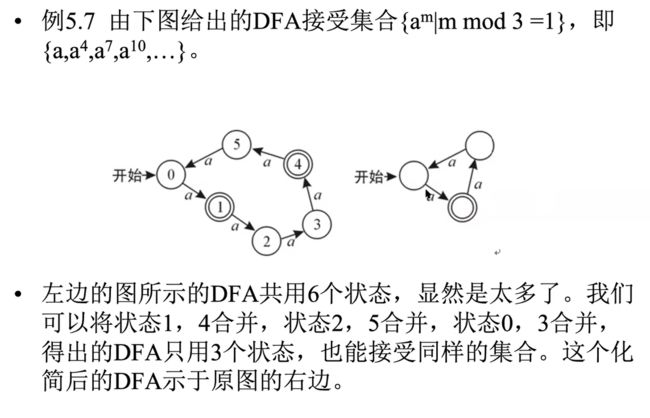
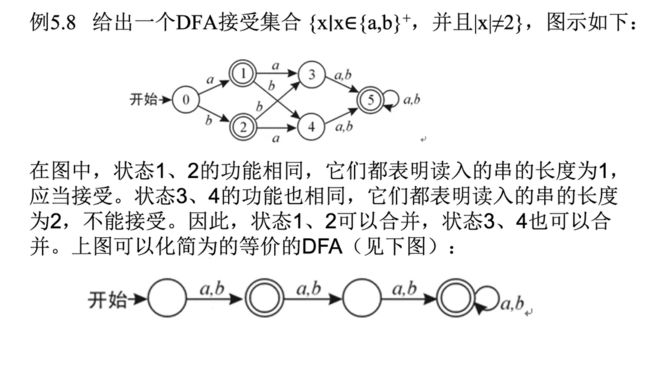
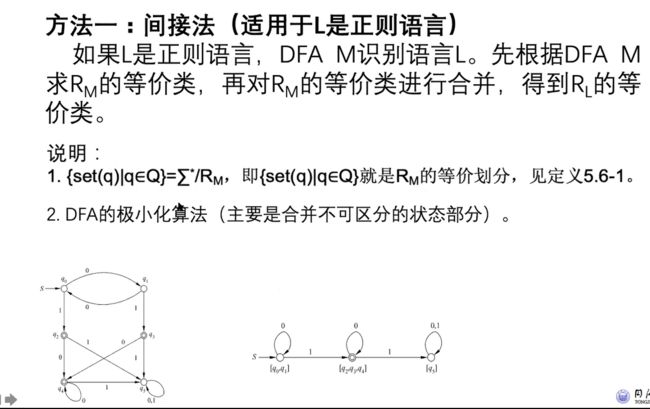
FA最小化
e.g1
e.g2
等价关系
e.g1
等价性
e.g1
e.g2
e.g3
右不变等价
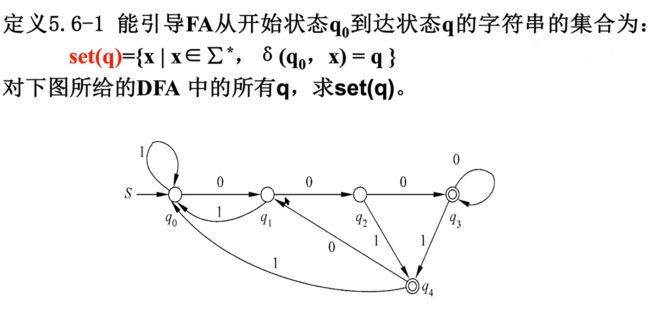
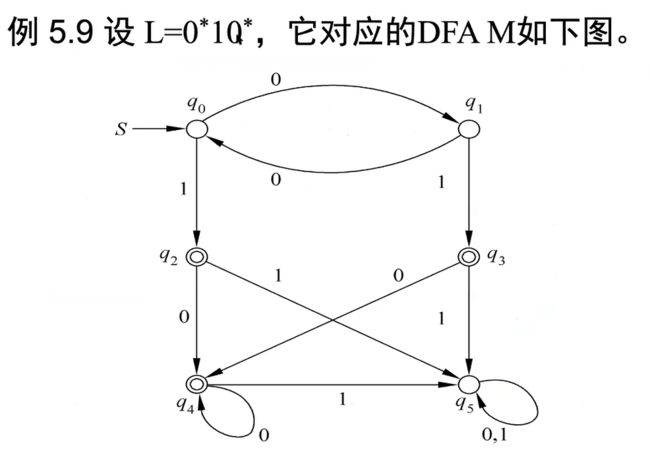
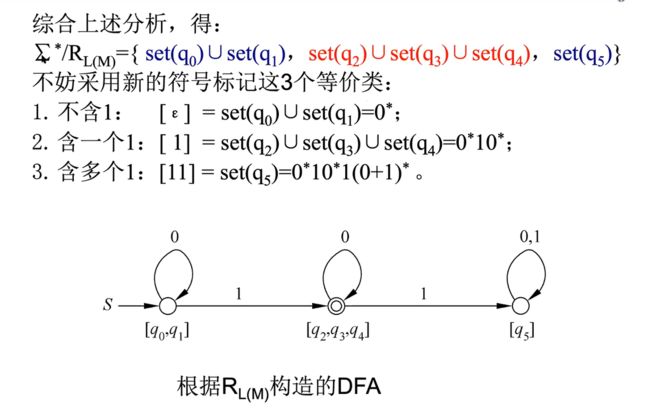
求RL的等价类
e.g2
e.g3
Myhill-Nerode定理*
应用
e.g1
光是考虑0都无穷了
DFA同构*
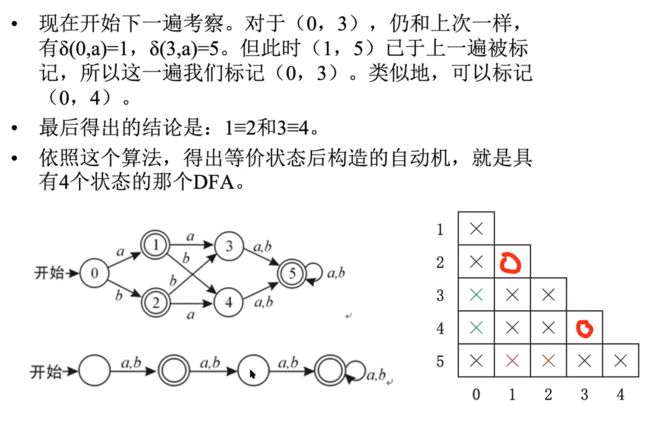
可区分 distinguishable
极小化算法
e.g1
e.g2