计算机导论02-计算机运算基础

数制及其转换

进位计数制

数码、基数、位权

术语	定义
数码	表示基本数值大小的不同数字符号。例如，十进制的数码有0、1、2、3、4、5、6、7、8、9。
基数	数制所使用的数码的个数。例如，十进制的基数为10。
位权	数码在不同位置上所代表的值不同，每个数码所表示的数值等于该数码乘以位权。在十进制中，数字6在十位数位置上表示60。每个位置的位权是与数码所在位置相关的常数。

N进制数制的特点

1. 基数为N： N进制数制的基数即为N，表示该数制所使用的数码的个数。

2. 数码范围： 共有0, 1, …, N-1共N个数码，最大的数码为N-1。此外，还包括一个符号“小数点”，用于表示小数部分。

3. 进位原则： N进制数制采用“逢N进一”的进位原则。当某一位的数码达到N时，就要向高位进位，并将该位的数码重新从0开始。这类似于十进制中当个位数达到9时，就进位到十位，重新从0开始。

计算机中常用的数制

数制	基数	数码	计数规则
十进制	10	0、1、2、3、4、5、6、7、8、9	逢10进1
二进制	2	0、1	逢2进1
八进制	8	0、1、2、3、4、5、6、7	逢8进1
十六进制	16	0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F	逢16进1（A、B、C、D、E、F对应10-15）

计算机使用二进制的原因

技术实现简便

1. 二进制中的0和1分别对应硬件中电路的接通和断开，电流的强弱，电位的高低等基本状态。这使得计算机硬件的设计和实现更加容易。

运算规则简单
二进制运算规则简单明确，例如二进制加法只有四种可能的结果：0、1、10、11，而二进制乘法也仅有0和1的组合。这简化了计算机中的运算过程。

二进制加法法则	二进制乘法法则
0+0=0, 0+1=1+0=1, 1+1=10	0×0=0, 0×1=1×0=0, 1×1=1

可靠性高
由于二进制计算规则简单，电路实现也相对简单，因此计算机硬件工作更为稳定，可靠性更高。

逻辑判断方便
二进制只有两个可能的状态，即0和1，与逻辑计算中的真假、True和False完美对应。这使得计算机在进行逻辑判断时更为方便和直观。

不同数制间的转换

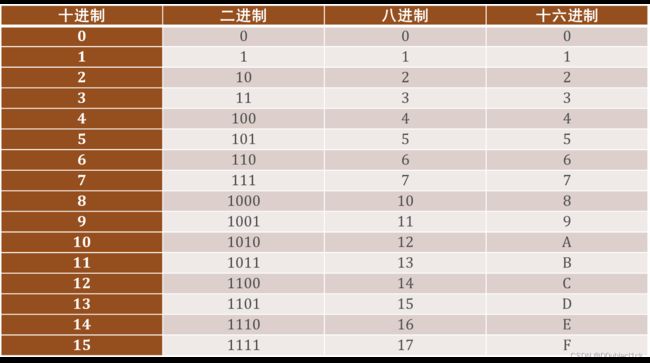
十进制与二进制、八进制、十六进制对应关系

图片来源教材配套课件

非常感谢你的提问！我理解你想要整理一下关于非十进制数转换为十进制数的笔记。以下是对你的笔记内容的整理：

非十进制数转换为十进制数

在计算机科学中，将非十进制数转换为十进制数的方法采用按位权展开再求和的方式。任何一个R进制数N（包括整数和小数部分）均可表示为如下形式：

其中：

例：

考虑二进制数 10001101.11转为十进制数：

=141.75

十进制转化成非十进制

除基取余法

除基取余，逆序排列，商零终止
除以基数取余数，逆序排列（先得到的余数排在低位，后得到的余数排在高位），商为零终止。用于整数部分

例

求：35转化成2进制

35的二进制为100011

乘基取整，顺序排列，余零终止
乘以基数取整数，顺序排列（先得到的整数排在高位，后得到的整数排在低位），余零终止（备注：十进制小数转换为非十进制小数的过程可能是无限的，即得不到余数为零的结果，此时根据有效数字的要求直接间断）

例：十进制0.25转化成二进制

整数及小数部分分别转换，结果用小数点连接

例：求十进制35.25的二进制
根据上面的结果，再相加为100011.01

二进制转化成八进制

转换原则
整数部分从低位到高位每三位为一组（不足3位在高位用0补足），小数部分从高位到低位每三位为一组（不足3位在低位用0补足），然后将每组三位二进制数转换成对应的一位八进制数。一组一组地转换成对应的八进制数，即得到转换的结果。

整、小独立，合三为一，不足补零
整数部分和小数部分分别独立转换，小数点向前或向后合三位二进制码为一位八进制码，不足三位的数码以零补足为三位

八进制	二进制
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

例：求二进制1001011.11101的八进制

八进制数转换为二进制数

整、小独立，一分为三
整数部分和小数部分分别独立转换，一位八进制码分成三位二进制码

例：八进制261.34转化成二进制

二进制和16进制转换

类似地，十六进制数与二进制数的转换原则是，十六进制数中的每一位用4位二进制数来表示。

十六进制	二进制
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
A	1010
B	1011
C	1100
D	1101
E	1110
F	1111

计算机中数据的表示

数的机器码表示

机器数和真值

1. 机器数
   • 用“0”表示正号，“1”表示负号，符号位在最高数值位之前。
   • 例如：[N1]原=01101101，[N2]原=11101101
2. 真值
   • 表示数的符号用“+”、“-”，与机器数不同。
   • N1=+1101101，N2=-1101101

原码

• 符号位为0表示正数，为1表示负数，数值部分用二进制数的绝对值表示。
• 例如：+59的原码为00111011，-59的原码为10111011。

注意：0的原码有两个值，分为“正零”和“负零”。

• [+0]原=00000000
• [-0]原=10000000

反码

• 为了便于求负数的补码。
• 正数的反码与原码相同，负数的反码是符号位不变，数值位逐位取反。

例如：[+59]反=[+59]原=00111011，[-59]反=11000100

补码

• 将某数X加上模数K，称为以K为模的X的补码。
• 正数的补码最高位为符号“0”，数值部分为该数本身。
• 负数的补码最高位为符号“1”，数值部分为用模减去该数的绝对值。

二进制数的补码简便求法：

• 正数的补码与其原码相同。
• 负数的补码是符号位不变，数值位逐位取反（求反码），然后在最低位加1（求反加1）。

例如：

• [+59]补=[+59]原=00111011
• [-59]原=10111011，[-59]反=11000100
• [-59]补=[-59]反+1=11000100+1=11000101

数值数据的表示

定点数表示

所谓定点格式，即约定机器中所有数据的小数点位置是固定不变的。通常将定点数据表示成纯小数或纯整数。为了将数表示成纯小数，通常把小数点固定在数值部分的最高位之前；而为了把数表示成纯整数，则把小数点固定在数值部分的最后面

浮点数表示

浮点表示法就是把一个数的有效数字和数的范围在计算机中分别予以表示。这种把数的范围和精度分别表示的方法，相当于数的小数点位置随比例因子的不同而在一定范围内自由浮动。因此称为浮点表示法。

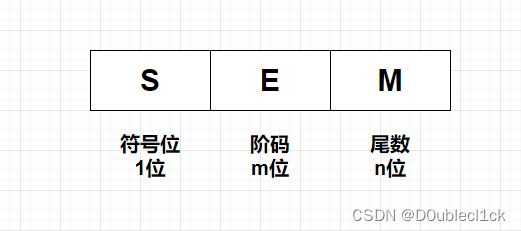
S为尾数的符号位，放在最高一位；E为阶码，紧跟在符号位之后，占m位；M为尾数，放在低位部分，占n位。

位数	类型	描述
1	符号	符号位，表示数字的正负
m	阶码	阶码位数，影响数字的大小
n	尾码	尾码位数，影响数字的精度
总计	64	机器字长总位数

设机器字长是64，则64 = 1 + m + n，
m越大，则n越小，X越大；阶码越大（越小），数的绝对值越大（越小），有效数字越少（越多），符合越大（越小）的数字精度越低（越高）的要求。

非数值数据的表示

西文字符的表示 - ASCII码

编码方法：
高三位（区号，0到7列），低四位（位号0到15行）
占用1B空间，8位二进制码的最高位（表示校验码，或ASCII的版本号）

二进制	十进制	十六进制	字符/缩写	解释
00000000	0	00	NUL (NULL)	空字符
00000001	1	01	SOH (Start Of Headling)	标题开始
00000010	2	02	STX (Start Of Text)	正文开始
00000011	3	03	ETX (End Of Text)	正文结束
00000100	4	04	EOT (End Of Transmission)	传输结束
00000101	5	05	ENQ (Enquiry)	请求
00000110	6	06	ACK (Acknowledge)	回应/响应/收到通知
00000111	7	07	BEL (Bell)	响铃
00001000	8	08	BS (Backspace)	退格
00001001	9	09	HT (Horizontal Tab)	水平制表符
00001010	10	0A	LF/NL(Line Feed/New Line)	换行键
00001011	11	0B	VT (Vertical Tab)	垂直制表符
00001100	12	0C	FF/NP (Form Feed/New Page)	换页键
00001101	13	0D	CR (Carriage Return)	回车键
00001110	14	0E	SO (Shift Out)	不用切换
00001111	15	0F	SI (Shift In)	启用切换
00010000	16	10	DLE (Data Link Escape)	数据链路转义
00010001	17	11	DC1/XON (Device Control 1/Transmission On)	设备控制1/传输开始
00010010	18	12	DC2 (Device Control 2)	设备控制2
00010011	19	13	DC3/XOFF (Device Control 3/Transmission Off)	设备控制3/传输中断
00010100	20	14	DC4 (Device Control 4)	设备控制4
00010101	21	15	NAK (Negative Acknowledge)	无响应/非正常响应/拒绝接收
00010110	22	16	SYN (Synchronous Idle)	同步空闲
00010111	23	17	ETB (End of Transmission Block)	传输块结束/块传输终止
00011000	24	18	CAN (Cancel)	取消
00011001	25	19	EM (End of Medium)	已到介质末端/介质存储已满/介质中断
00011010	26	1A	SUB (Substitute)	替补/替换
00011011	27	1B	ESC (Escape)	逃离/取消
00011100	28	1C	FS (File Separator)	文件分割符
00011101	29	1D	GS (Group Separator)	组分隔符/分组符
00011110	30	1E	RS (Record Separator)	记录分离符
00011111	31	1F	US (Unit Separator)	单元分隔符
00100000	32	20	(Space)	空格
00100001	33	21	!
00100010	34	22	"
00100011	35	23	#
00100100	36	24	$
00100101	37	25	%
00100110	38	26	&
00100111	39	27	’
00101000	40	28	(
00101001	41	29	)
00101010	42	2A	*
00101011	43	2B	+
00101100	44	2C	,
00101101	45	2D	-
00101110	46	2E	.
00101111	47	2F	/
00110000	48	30	0
00110001	49	31	1
00110010	50	32	2
00110011	51	33	3
00110100	52	34	4
00110101	53	35	5
00110110	54	36	6
00110111	55	37	7
00111000	56	38	8
00111001	57	39	9
00111010	58	3A	:
00111011	59	3B	;
00111100	60	3C	<
00111101	61	3D	=
00111110	62	3E	>
00111111	63	3F	?
01000000	64	40	@
01000001	65	41	A
01000010	66	42	B
01000011	67	43	C
01000100	68	44	D
01000101	69	45	E
01000110	70	46	F
01000111	71	47	G
01001000	72	48	H
01001001	73	49	I
01001010	74	4A	J
01001011	75	4B	K
01001100	76	4C	L
01001101	77	4D	M
01001110	78	4E	N
01001111	79	4F	O
01010000	80	50	P
01010001	81	51	Q
01010010	82	52	R
01010011	83	53	S
01010100	84	54	T
01010101	85	55	U
01010110	86	56	V
01010111	87	57	W
01011000	88	58	X
01011001	89	59	Y
01011010	90	5A	Z
01011011	91	5B	[
01011100	92	5C	\
01011101	93	5D	]
01011110	94	5E	^
01011111	95	5F	_
01100000	96	60	`
01100001	97	61	a
01100010	98	62	b
01100011	99	63	c
01100100	100	64	d
01100101	101	65	e
01100110	102	66	f
01100111	103	67	g
01101000	104	68	h
01101001	105	69	i
01101010	106	6A	j
01101011	107	6B	k
01101100	108	6C	l
01101101	109	6D	m
01101110	110	6E	n
01101111	111	6F	o
01110000	112	70	p
01110001	113	71	q
01110010	114	72	r
01110011	115	73	s
01110100	116	74	t
01110101	117	75	u
01110110	118	76	v
01110111	119	77	w
01111000	120	78	x
01111001	121	79	y
01111010	122	7A	z
01111011	123	7B	{
01111100	124	7C	|
01111101	125	7D	}
01111110	126	7E	~

汉字的表示

• GB2312字符集。
• BIG5字符集。
• GBK字符集。
• GB18030字符集。

汉字编码占用2B空间，区位码，国标码，机内码；
GB18030-2000字符集

Unicode码

Unicode为每种语言中的每个字符设定了统一并且唯一的二进制编码，以满足跨语言、跨平台进行文本转换、处理的要求。

Universal-code：通用编码，统一编码，16位字符集，每个字符占2B空间，计可表示216个不同字符，可扩展到32位字符集。

数据存储与数据运算

数据存储

存储单元

在计算机中最小的信息单位是bit，也就是一个二进制位（b），8个bit组成一个Byte，也就是字节（B）。一个存储单元（memory cell）可以存储一个字节，也就是8个二进制位。
存储单元的地址称为存储地址（memory address），一般用十六进制数表示，从0开始顺序编号。

数据的存储单位

中文单位	中文简称	英文单位	英文简称
字节	字节	Byte	B
千字节	开	KiloByte	KB
兆字节	兆	MegaByte	MB
吉字节	吉	GigaByte	GB
太字节	太	TeraByte	TB
拍字节	拍	PetaByte	PB
艾字节	艾	ExaByte	EB
泽字节	泽	ZettaByte	ZB
尧字节	尧	YottaByte	YB

数据运算

定点加、减法运算

定点加、减法运算属于算术运算，要考虑参加运算数据的符号和编码格式。在计算机中，定点数据主要有原码、反码、补码三种形式。

补码运算时，可以将符号位与数值位一起处理，因此，现代计算机的运算器一般都采用补码形式进行加减法运算。

（1）补码加法
补码加法的公式是：
[x]补+[y]补=[x+y]补

（2）补码减法
由于减去一个数就是加上这个数的负数，因此
[x-y]补=[x+(-y)]补=[x]补+[-y]补

从[y]补求[-y]补的法则：当已知[y]补要求[-y]补时，只要将[y]补连同符号位“取反且最低位加1”即可。

（3）溢出及其判断
如果两数进行加减运算之后的运算结果超出了给定的取值范围，这就称为溢出。
正溢: 两个正数相加，结果大于机器所能表示的最大正数
负溢: 两个负数相加，结果小于机器所能表示的最小负数

定点乘除法运算

实现乘除法运算的方式主要有三种：

1. 软件实现： 通过编写软件算法来完成乘除法运算。

2. 硬件实现（基本运算电路的增强）： 在原有的基本运算电路基础上，引入左右移位和计数器等逻辑电路，同时增加专门的乘除法指令，以实现乘除法运算。

3. 硬件实现（单元阵列乘除法器）： 随着大规模集成电路的发展，出现了高速的单元阵列乘除法器。这些乘除法器采用并行计算的方式，通过流水线处理乘除法运算，也可以通过专门的乘除法指令来调用。

逻辑运算

• 逻辑非运算（NOT）
• 逻辑与运算（AND）
• 逻辑或运算（OR）
• 逻辑异或运算（XOR）