递归的递归之书：第十章到第十四章

十、文件查找器

原文：Chapter 10 - File Finder

译者：飞龙

协议：CC BY-NC-SA 4.0

在本章中，你将编写自己的递归程序，根据自定义需求搜索文件。你的计算机已经有一些文件搜索命令和应用程序，但通常它们只能根据部分文件名检索文件。如果你需要进行奇特、高度特定的搜索怎么办？例如，如果你需要找到所有具有偶数字节的文件，或者文件名包含每个元音字母的文件？

你可能永远不需要专门进行这些搜索，但是你可能会有奇怪的搜索条件。如果你不能自己编写这个搜索，你就会很倒霉。

正如你所学到的，递归特别适用于具有树状结构的问题。你的计算机上的文件系统就像一棵树，就像你在图 2-6 中看到的那样。每个文件夹都分成子文件夹，这些子文件夹又可以分成其他子文件夹。我们将编写一个递归函数来遍历这棵树。

完整的文件搜索程序

让我们首先看一下递归文件搜索程序的完整源代码。本章的其余部分将逐个解释代码的每个部分。将文件搜索程序的源代码复制到名为fileFinder.py的文件中：

import os

def hasEvenByteSize(fullFilePath):
    """Returns True if fullFilePath has an even size in bytes,
    otherwise returns False."""
    fileSize = os.path.getsize(fullFilePath)
    return fileSize % 2 == 0

def hasEveryVowel(fullFilePath):
    """Returns True if the fullFilePath has a, e, i, o, and u,
    otherwise returns False."""
    name = os.path.basename(fullFilePath).lower()
    return ('a' in name) and ('e' in name) and ('i' in name) and ('o' in name) and ('u' in name)

def walk(folder, matchFunc):
    """Calls the match function with every file in the folder and its
    subfolders. Returns a list of files that the match function
    returned True for."""
    matchedFiles = [] # This list holds all the matches.
    folder = os.path.abspath(folder) # Use the folder's absolute path.

    # Loop over every file and subfolder in the folder:
    for name in os.listdir(folder):
        filepath = os.path.join(folder, name)
        if os.path.isfile(filepath):
            # Call the match function for each file:
            if matchFunc(filepath):
                matchedFiles.append(filepath)
        elif os.path.isdir(filepath):
            # Recursively call walk for each subfolder, extending
            # the matchedFiles with their matches:
            matchedFiles.extend(walk(filepath, matchFunc))
    return matchedFiles

print('All files with even byte sizes:')
print(walk('.', hasEvenByteSize))
print('All files with every vowel in their name:')
print(walk('.', hasEveryVowel))

文件搜索程序的主要函数是walk()，它在基本文件夹及其子文件夹中“遍历”整个文件范围。它调用另外两个实现自定义搜索条件的函数中的一个。在这个程序的上下文中，我们将这些称为匹配函数。匹配函数调用返回True，如果文件符合搜索条件；否则，返回False。

walk()函数的工作是为它遍历的每个文件夹中的每个文件调用匹配函数。让我们更详细地看一下代码。

匹配函数

在 Python 中，你可以将函数本身作为参数传递给函数调用。在下面的示例中，callTwice()函数调用其函数参数两次，无论是sayHello()还是sayGoodbye()：

Python

>>> def callTwice(func):
...     func()
...     func()
...
>>> def sayHello():
...     print('Hello!')
...
>>> def sayGoodbye():
...     print('Goodbye!')
...
>>> callTwice(sayHello)
Hello!
Hello!
>>> callTwice(sayGoodbye)
Goodbye!
Goodbye!

callTwice()函数调用作为func参数传递给它的任何函数。请注意，我们从函数参数中省略了括号，而是写成callTwice(sayHello)，而不是callTwice(sayHello())。这是因为我们传递的是sayHello()函数本身，而不是调用sayHello()并传递其返回值。

walk()函数接受一个匹配函数参数作为其搜索条件。这使我们能够自定义文件搜索的行为，而无需修改walk()函数本身的代码。我们稍后会看一下walk()。首先，让我们看一下程序中的两个示例匹配函数。

查找具有偶数字节的文件

第一个匹配函数找到具有偶数字节大小的文件：

Python

import os

def hasEvenByteSize(fullFilePath):
    """Returns True if fullFilePath has an even size in bytes,
    otherwise returns False."""
    fileSize = os.path.getsize(fullFilePath)
    return fileSize % 2 == 0

我们导入os模块，该模块在整个程序中用于通过getsize()、basename()等函数获取有关计算机上文件的信息。然后我们创建一个名为hasEvenByteSize()的匹配函数。所有匹配函数都接受一个名为fullFilePath的字符串参数，并返回True或False来表示匹配或不匹配。

os.path.getsize()函数确定fullFilePath中文件的大小（以字节为单位）。然后我们使用%模运算符来确定这个数字是否是偶数。如果是偶数，return语句返回True；如果是奇数，返回False。例如，让我们考虑 Windows 操作系统中附带的记事本应用程序的大小（在 macOS 或 Linux 上，尝试在*/bin/ls*程序上运行这个函数）：

Python

>>> import os
>>> os.path.getsize('C:/Windows/system32/notepad.exe')
211968
>>> 211968 % 2 == 0
True

hasEvenByteSize()匹配函数可以使用任何 Python 函数来查找有关fullFilePath文件的更多信息。这使您能够为任何搜索条件编写代码。当walk()对文件夹和子文件夹中的每个文件调用匹配函数时，匹配函数会为每个文件返回True或False。这告诉walk()文件是否匹配。

查找包含所有元音字母的文件名

让我们来看下一个匹配函数：

def hasEveryVowel(fullFilePath):
    """Returns True if the fullFilePath has a, e, i, o, and u,
    otherwise returns False."""
    name = os.path.basename(fullFilePath).lower()
    return ('a' in name) and ('e' in name) and ('i' in name) and ('o' in name) and ('u' in name)

我们调用os.path.basename()来从文件路径中删除文件夹名称。Python 对字符串进行区分大小写的比较，这确保了hasEveryVowel()不会因为文件名中的元音字母是大写而漏掉任何元音字母。例如，调用os.path.basename('C:/Windows/system32/notepad.exe')返回字符串notepad.exe。这个字符串的lower()方法调用返回字符串的小写形式，这样我们只需要检查其中的小写元音字母。本章后面的“用于处理文件的有用 Python 标准库函数”探讨了一些更多用于获取文件信息的函数。

我们使用一个带有长表达式的return语句，如果name包含a、e、i、o或u，则表达式求值为True，表示文件符合搜索条件。否则，return语句返回False。

递归walk()函数

匹配函数检查文件是否符合搜索条件，而walk()函数找到所有要检查的文件。递归的walk()函数会传入一个要搜索的基础文件夹的名称，以及一个要对文件夹中的每个文件调用的匹配函数。

walk()函数也会递归地对基础文件夹中的每个子文件夹进行调用。这些子文件夹成为递归调用中的基础文件夹。让我们对这个递归函数提出三个问题：

1. 什么是基本情况？当函数完成对给定基础文件夹中的每个文件和子文件夹的处理时。

2. 递归函数调用传递了什么参数？要搜索的基础文件夹和用于查找匹配文件的匹配函数。对于该文件夹中的每个子文件夹，都会使用子文件夹作为新的文件夹参数进行递归调用。

3. 这个参数如何变得更接近基本情况？最终，函数要么在所有子文件夹上递归调用自身，要么遇到没有任何子文件夹的基础文件夹。

图 10-1 显示了一个示例文件系统以及对walk()的递归调用，它以C:\为基础文件夹进行调用。

图 10-1：一个示例文件系统和递归的walk()函数对其的调用

让我们来看一下walk()函数的代码：

def walk(folder, matchFunc):
    """Calls the match function with every file in the folder and its
    subfolders. Returns a list of files that the match function
    returned True for."""
    matchedFiles = [] # This list holds all the matches.
    folder = os.path.abspath(folder) # Use the folder's absolute path.

walk()函数有两个参数：folder是要搜索的基础文件夹的字符串（我们可以传入’.'来指代 Python 程序所在的当前文件夹），matchFunc是一个 Python 函数，它接受一个文件名并在函数说它是搜索匹配时返回True。否则，函数返回False。

函数的下一部分检查folder的内容：

Python

 # Loop over every file and subfolder in the folder:
    for name in os.listdir(folder):
        filepath = os.path.join(folder, name)
        if os.path.isfile(filepath):

for循环调用os.listdir()返回folder文件夹内容的列表。此列表包括所有文件和子文件夹。对于每个文件，我们通过将文件夹与文件或文件夹的名称连接起来创建完整的绝对路径。如果名称指的是文件，则os.path.isfile()函数调用返回True，我们将检查文件是否是搜索匹配项：

Python

 # Call the match function for each file:
            if matchFunc(filepath):
                matchedFiles.append(filepath)

我们调用匹配函数，将for循环当前文件的完整绝对文件路径传递给它。请注意，matchFunc是walk()的一个参数的名称。如果hasEvenByteSize()，hasEveryVowel()或另一个函数作为matchFunc参数的参数传递，则walk()将调用该函数。如果filepath包含根据匹配算法匹配的文件，则将其添加到matches列表中：

Python

 elif os.path.isdir(filepath):
            # Recursively call walk for each subfolder, extending
            # the matchedFiles with their matches:
            matchedFiles.extend(walk(filepath, matchFunc))

否则，如果for循环的文件是子文件夹，则os.path.isdir()函数调用返回True。然后我们将子文件夹传递给递归函数调用。递归调用返回子文件夹（及其子文件夹）中所有匹配文件的列表，然后将其添加到matches列表中：

 return matchedFiles

for循环完成后，matches列表包含此文件夹（及其所有子文件夹）中的所有匹配文件。此列表成为walk()函数的返回值。

调用 walk()函数

现在我们已经实现了walk()函数和一些匹配函数，我们可以运行我们自定义的文件搜索。我们将'.'字符串作为walk()的第一个参数传递，这是一个特殊的目录名称，表示当前目录，以便它使用程序运行的文件夹作为基本文件夹进行搜索：

Python

print('All files with even byte sizes:')
print(walk('.', hasEvenByteSize))
print('All files with every vowel in their name:')
print(walk('.', hasEveryVowel))

此程序的输出取决于计算机上的文件，但这演示了您如何为任何搜索条件编写代码。例如，输出可能如下所示：

Python

All files with even byte sizes:
['C:\\Path\\accesschk.exe', 'C:\\Path\\accesschk64.exe', 
'C:\\Path\\AccessEnum.exe', 'C:\\Path\\ADExplorer.exe', 
'C:\\Path\\Bginfo.exe', 'C:\\Path\\Bginfo64.exe', 
'C:\\Path\\diskext.exe', 'C:\\Path\\diskext64.exe', 
'C:\\Path\\Diskmon.exe', 'C:\\Path\\DiskView.exe', 
'C:\\Path\\hex2dec64.exe', 'C:\\Path\\jpegtran.exe', 
'C:\\Path\\Tcpview.exe', 'C:\\Path\\Testlimit.exe', 
'C:\\Path\\wget.exe', 'C:\\Path\\whois.exe']
All files with every vowel in their name:
['C:\\Path\\recursionbook.bat']

用于处理文件的有用的 Python 标准库函数

让我们看看一些函数，这些函数在编写自己的匹配函数时可能会对您有所帮助。Python 附带的标准库模块中有几个有用的函数，用于获取有关文件的信息。其中许多位于os和shutil模块中，因此您的程序必须在调用这些函数之前运行import os或import shutil。

查找有关文件名称的信息

传递给匹配函数的完整文件路径可以使用os.path.basename()和os.path.dirname()函数分解为基本名称和目录名称。您还可以调用os.path.split()将这些名称作为元组获取。在 Python 的交互式 shell 中输入以下内容。在 macOS 或 Linux 上，尝试使用/bin/ls作为文件名：

Python

>>> import os
>>> filename = 'C:/Windows/system32/notepad.exe'
>>> os.path.basename(filename)
'notepad.exe'
>>> os.path.dirname(filename)
'C:/Windows/system32'
>>> os.path.split(filename)
('C:/Windows/system32', 'notepad.exe')
>>> folder, file = os.path.split(filename)
>>> folder
'C:/Windows/system32'
>>> file
'notepad.exe'

您可以在这些字符串值上使用 Python 的任何字符串方法来帮助评估文件是否符合您的搜索条件，例如hasEveryVowel()匹配函数中的lower()。

查找有关文件时间戳的信息

文件具有指示它们创建时间、上次修改时间和上次访问时间的时间戳。Python 的os.path.getctime()，os.path.getmtime()和os.path.getatime()分别将这些时间戳作为浮点值返回，指示自Unix 纪元以来的秒数，即 1970 年 1 月 1 日协调世界时（UTC）时区的午夜。在交互式 shell 中输入以下内容：

Python

> import os
> filename = 'C:/Windows/system32/notepad.exe'
> os.path.getctime(filename)
1625705942.1165037
> os.path.getmtime(filename)
1625705942.1205275
> os.path.getatime(filename)
1631217101.8869188

这些浮点值对程序来说很容易使用，因为它们只是单个数字，但您需要使用 Python 的time模块中的函数使它们对人类更容易阅读。time.localtime()函数将 Unix 纪元时间戳转换为计算机所在时区的struct_time对象。struct_time对象具有几个属性，其名称以tm_开头，用于获取日期和时间信息。在交互式 shell 中输入以下内容：

Python

>>> import os
>>> filename = 'C:/Windows/system32/notepad.exe'
>>> ctimestamp = os.path.getctime(filename)
>>> import time
>>> time.localtime(ctimestamp)
time.struct_time(tm_year=2021, tm_mon=7, tm_mday=7, tm_hour=19, 
tm_min=59, tm_sec=2, tm_wday=2, tm_yday=188, tm_isdst=1)
>>> st = time.localtime(ctimestamp)
>>> st.tm_year
2021
>>> st.tm_mon
7
>>> st.tm_mday
7
>>> st.tm_wday
2
>>> st.tm_hour
19
>>> st.tm_min
59
>>> st.tm_sec
2

请注意，tm_mday属性是月份的日期，范围是1到31。tm_wday属性是星期几，从星期一的0开始，星期二的1，依此类推，直到星期日的6。

如果需要time_struct对象的简短、可读的字符串，请将其传递给time.asctime()函数：

Python

>>> import os
>>> filename = 'C:/Windows/system32/notepad.exe'
>>> ctimestamp = os.path.getctime(filename)
>>> import time
>>> st = time.localtime(ctimestamp)
>>> time.asctime(st)
'Wed Jul  7 19:59:02 2021'

而time.localtime()函数返回本地时区的struct_time对象，time.gmtime()函数返回 UTC 或格林威治标准时间时区的struct_time对象。将以下内容输入交互式 shell：

Python

>>> import os
>>> filename = 'C:/Windows/system32/notepad.exe'
>>> ctimestamp = os.path.getctime(filename)
>>> import time
>>> ctimestamp = os.path.getctime(filename)
>>> time.localtime(ctimestamp)
time.struct_time(tm_year=2021, tm_mon=7, tm_mday=7, tm_hour=19, 
tm_min=59, tm_sec=2, tm_wday=2, tm_yday=188, tm_isdst=1)
>>> time.gmtime(ctimestamp)
time.struct_time(tm_year=2021, tm_mon=7, tm_mday=8, tm_hour=0, 
tm_min=59, tm_sec=2, tm_wday=3, tm_yday=189, tm_isdst=0)

这些os.path函数（返回 Unix 纪元时间戳）与time函数（返回struct_time对象）之间的交互可能会令人困惑。图 10-2 显示了从文件名字符串开始的代码链，以获取时间戳的各个部分。

图 10-2：从文件名到时间戳的各个属性

最后，time.time()函数返回自 Unix 纪元以来到当前时间的秒数。

修改您的文件

walk()函数返回与您的搜索条件匹配的文件列表后，您可能希望对它们进行重命名、删除或执行其他操作。Python 标准库中的shutil和os模块具有执行此操作的函数。此外，第三方模块send2trash也可以将文件发送到操作系统的回收站，而不是永久删除它们。

要移动文件，请使用shutil.move()函数并提供两个参数。第一个参数是要移动的文件，第二个是要将其移动到的文件夹。例如，您可以调用以下内容：

Python

>>> import shutil
>>> shutil.move('spam.txt', 'someFolder')
'someFolder\\spam.txt'

shutil.move()函数返回文件的新文件路径字符串。您还可以指定文件名以同时移动和重命名文件：

Python

>>> import shutil
>>> shutil.move('spam.txt', 'someFolder\\newName.txt')
'someFolder\\newName.txt'

如果第二个参数缺少文件夹，您可以只指定一个新名称以在当前文件夹中重命名文件：

Python

>>> import shutil
>>> shutil.move('spam.txt', 'newName.txt')
'newName.txt'

请注意，shutil.move()函数既移动又重命名文件，类似于 Unix 和 macOS 的mv命令移动和重命名文件。没有单独的shutil.rename()函数。

要复制文件，请使用shutil.copy()函数并提供两个参数。第一个参数是要复制的文件的文件名，第二个参数是副本的新名称。例如，您可以调用以下内容：

Python

>>> import shutil
>>> shutil.copy('spam.txt', 'spam-copy.txt')
'spam-copy.txt'

shutil.copy()函数返回副本的名称。要删除文件，请调用os.unlink()函数并将要删除的文件的名称传递给它：

Python

>>> import os
>>> os.unlink('spam.txt')
>>>

使用unlink而不是delete的名称是因为它删除了与文件链接的文件名的技术细节。但由于大多数文件只有一个链接的文件名，这种取消链接也会删除文件。如果您不理解这些文件系统概念，也没关系，只需知道os.unlink()会删除文件。

调用os.unlink()会永久删除文件，如果程序中的错误导致函数删除错误的文件，这可能是危险的。相反，您可以使用send2trash模块的send2trash()函数将文件放入操作系统的回收站。要安装此模块，请在 Windows 命令提示符上运行run python -m pip install --user send2trash，或在 macOS 或 Linux 终端上运行run python3 -m pip install。安装模块后，您将能够使用import send2trash导入它。

将以下内容输入交互式 shell：

Python

>>> open('deleteme.txt', 'w').close() # Create a blank file.
>>> import send2trash
>>> send2trash.send2trash('deleteme.txt')

此示例创建一个名为deleteme.txt的空文件。调用send2trash.send2trash()（模块和函数同名），此文件将被移除到回收站。

摘要

本章的文件搜索项目使用递归来“遍历”文件夹及其所有子文件夹的内容。文件查找程序的walk()函数递归地导航这些文件夹，将自定义搜索条件应用于每个子文件夹中的每个文件。搜索条件被实现为匹配函数，这些函数被传递给walk()函数。这使我们能够通过编写新函数而不是修改walk()中的代码来更改搜索条件。

我们的项目有两个匹配函数，用于查找文件大小为偶数字节或包含其名称中的每个元音字母，但您可以编写自己的函数传递给walk()。这就是编程的力量；您可以为自己的需求创建商业应用程序中不可用的功能。

进一步阅读

Python 内置的os.walk()函数的文档（类似于文件查找器项目中的walk()函数）位于docs.python.org/3/library/os.html#os.walk。您还可以在我的书Automate the Boring Stuff with Python第九章中了解有关计算机文件系统和 Python 文件函数的更多信息，第 2 版（No Starch Press，2019）位于automatetheboringstuff.com/2e/chapter9。

Python 标准库中的datetime模块还有更多与时间戳数据交互的方法。您可以在Automate the Boring Stuff with Python第十七章中了解更多信息，第 2 版位于automatetheboringstuff.com/2e/chapter17。

十一、迷宫生成器

原文：Chapter 11 - Maze Generator

译者：飞龙

协议：CC BY-NC-SA 4.0

第四章描述了一个解决迷宫的递归算法，但另一个递归算法生成迷宫。在本章中，我们将以第四章中迷宫求解程序相同的格式生成迷宫。因此，无论您是迷宫的解决者还是创建者，现在您都有能力将编程应用于此任务。

该算法通过访问迷宫中的一个起始空间，然后递归地访问相邻的空间来工作。随着算法继续访问相邻空间，迷宫的走廊被“刻出”。如果算法到达没有相邻空间的死胡同，它会回溯到先前的空间，直到找到一个未访问的相邻空间，并继续从那里访问。当算法回溯到起始空间时，整个迷宫已经生成。

我们将在这里使用的递归回溯算法生成的迷宫倾向于具有长走廊（连接分支交叉点的迷宫空间）并且相当容易解决。但是，这种算法比许多其他迷宫生成算法（如 Kruskal 算法或 Wilson 算法）更容易实现，因此它是该主题的很好介绍。

完整的迷宫生成器程序

让我们首先看一下程序的完整 Python 和 JavaScript 源代码，该程序使用递归回溯算法生成迷宫。本章的其余部分将逐个解释代码的每个部分。

将此 Python 代码复制到名为mazeGenerator.py的文件中：

Python

import random

WIDTH = 39 # Width of the maze (must be odd).
HEIGHT = 19 # Height of the maze (must be odd).
assert WIDTH % 2 == 1 and WIDTH >= 3
assert HEIGHT % 2 == 1 and HEIGHT >= 3
SEED = 1
random.seed(SEED)

# Use these characters for displaying the maze:
EMPTY = ' '
MARK = '@'
WALL = chr(9608) # Character 9608 is '█'
NORTH, SOUTH, EAST, WEST = 'n', 's', 'e', 'w'

# Create the filled-in maze data structure to start: 
maze = {}
for x in range(WIDTH):
    for y in range(HEIGHT):
        maze[(x, y)] = WALL # Every space is a wall at first.

def printMaze(maze, markX=None, markY=None):
    """Displays the maze data structure in the maze argument. The
    markX and markY arguments are coordinates of the current
    '@' location of the algorithm as it generates the maze."""

    for y in range(HEIGHT):
        for x in range(WIDTH):
            if markX == x and markY == y:
                # Display the '@' mark here:
                print(MARK, end='')
            else:
                # Display the wall or empty space:
                print(maze[(x, y)], end='')
        print() # Print a newline after printing the row.

def visit(x, y):
    """"Carve out" empty spaces in the maze at x, y and then
    recursively move to neighboring unvisited spaces. This
    function backtracks when the mark has reached a dead end."""
 maze[(x, y)] = EMPTY # "Carve out" the space at x, y.
    printMaze(maze, x, y) # Display the maze as we generate it.
    print('\n\n')

    while True:
        # Check which neighboring spaces adjacent to
        # the mark have not been visited already:
        unvisitedNeighbors = []
        if y > 1 and (x, y - 2) not in hasVisited:
            unvisitedNeighbors.append(NORTH)

        if y < HEIGHT - 2 and (x, y + 2) not in hasVisited:
            unvisitedNeighbors.append(SOUTH)

        if x > 1 and (x - 2, y) not in hasVisited:
            unvisitedNeighbors.append(WEST)

        if x < WIDTH - 2 and (x + 2, y) not in hasVisited:
            unvisitedNeighbors.append(EAST)

        if len(unvisitedNeighbors) == 0:
            # BASE CASE
            # All neighboring spaces have been visited, so this is a
            # dead end. Backtrack to an earlier space:
            return
        else:
            # RECURSIVE CASE
            # Randomly pick an unvisited neighbor to visit:
            nextIntersection = random.choice(unvisitedNeighbors)

            # Move the mark to an unvisited neighboring space:

            if nextIntersection == NORTH:
                nextX = x
                nextY = y - 2
                maze[(x, y - 1)] = EMPTY # Connecting hallway.
            elif nextIntersection == SOUTH:
                nextX = x
                nextY = y + 2
                maze[(x, y + 1)] = EMPTY # Connecting hallway.
            elif nextIntersection == WEST:
                nextX = x - 2
                nextY = y
                maze[(x - 1, y)] = EMPTY # Connecting hallway.
            elif nextIntersection == EAST:
                nextX = x + 2
                nextY = y
                maze[(x + 1, y)] = EMPTY # Connecting hallway.

            hasVisited.append((nextX, nextY)) # Mark as visited.
            visit(nextX, nextY) # Recursively visit this space.

# Carve out the paths in the maze data structure:
hasVisited = [(1, 1)] # Start by visiting the top-left corner.
visit(1, 1)

# Display the final resulting maze data structure:
printMaze(maze)

将此 JavaScript 代码复制到名为mazeGenerator.html的文件中：

JavaScript

<script type="text/javascript">

const WIDTH = 39; // Width of the maze (must be odd).
const HEIGHT = 19; // Height of the maze (must be odd).
console.assert(WIDTH % 2 == 1 && WIDTH >= 2);
console.assert(HEIGHT % 2 == 1 && HEIGHT >= 2);

// Use these characters for displaying the maze:
const EMPTY = " ";
const MARK = "@";
const WALL = "█"; // Character 9608 is ′█′
const [NORTH, SOUTH, EAST, WEST] = ["n", "s", "e", "w"];

// Create the filled-in maze data structure to start:
let maze = {};
for (let x = 0; x < WIDTH; x++) {
    for (let y = 0; y < HEIGHT; y++) {
        maze[[x, y]] = WALL; // Every space is a wall at first.
    }
}

function printMaze(maze, markX, markY) {
    // Displays the maze data structure in the maze argument. The
    // markX and markY arguments are coordinates of the current
    // '@' location of the algorithm as it generates the maze.
    document.write('');
    for (let y = 0; y < HEIGHT; y++) {
        for (let x = 0; x < WIDTH; x++) {
            if (markX === x && markY === y) {
                // Display the ′@′ mark here:
                document.write(MARK);
            } else {
                // Display the wall or empty space:
                document.write(maze[[x, y]]);
            }
        }
        document.write('
'); // Print a newline after printing the row.
    }
    document.write('');
}

function visit(x, y) {
    // "Carve out" empty spaces in the maze at x, y and then
    // recursively move to neighboring unvisited spaces. This
    // function backtracks when the mark has reached a dead end.

 maze[[x, y]] = EMPTY; // "Carve out" the space at x, y.
    printMaze(maze, x, y); // Display the maze as we generate it.
    document.write('


');

    while (true) {
        // Check which neighboring spaces adjacent to
        // the mark have not been visited already:
        let unvisitedNeighbors = [];
        if (y > 1 && !JSON.stringify(hasVisited).includes(JSON.stringify([x, y - 2]))) {
            unvisitedNeighbors.push(NORTH);
        }
        if (y < HEIGHT - 2 && 
        !JSON.stringify(hasVisited).includes(JSON.stringify([x, y + 2]))) {
            unvisitedNeighbors.push(SOUTH);
        }
        if (x > 1 && 
        !JSON.stringify(hasVisited).includes(JSON.stringify([x - 2, y]))) {
            unvisitedNeighbors.push(WEST);
        }
        if (x < WIDTH - 2 && 
        !JSON.stringify(hasVisited).includes(JSON.stringify([x + 2, y]))) {
            unvisitedNeighbors.push(EAST);
        }

        if (unvisitedNeighbors.length === 0) {
            // BASE CASE
            // All neighboring spaces have been visited, so this is a
            // dead end. Backtrack to an earlier space:
            return;
        } else {
            // RECURSIVE CASE
            // Randomly pick an unvisited neighbor to visit:
            let nextIntersection = unvisitedNeighbors[
            Math.floor(Math.random() * unvisitedNeighbors.length)];

            // Move the mark to an unvisited neighboring space:
            let nextX, nextY;
            if (nextIntersection === NORTH) {
                nextX = x;
                nextY = y - 2;
                maze[[x, y - 1]] = EMPTY; // Connecting hallway.
            } else if (nextIntersection === SOUTH) {
                nextX = x;
                nextY = y + 2;
                maze[[x, y + 1]] = EMPTY; // Connecting hallway.
            } else if (nextIntersection === WEST) {
                nextX = x - 2;
                nextY = y;
                maze[[x - 1, y]] = EMPTY; // Connecting hallway.
            } else if (nextIntersection === EAST) {
                nextX = x + 2;
                nextY = y;
                maze[[x + 1, y]] = EMPTY; // Connecting hallway.
            }
 hasVisited.push([nextX, nextY]); // Mark space as visited.
            visit(nextX, nextY); // Recursively visit this space.
        }
    }
}

// Carve out the paths in the maze data structure:
let hasVisited = [[1, 1]]; // Start by visiting the top-left corner.
visit(1, 1);

// Display the final resulting maze data structure:
printMaze(maze);
</script>

当您运行此程序时，它会产生大量文本，将填满终端窗口或浏览器，并显示迷宫构建的每一步。您将不得不向上滚动以查看整个输出。

迷宫数据结构开始时是一个完全填满的二维空间。递归回溯算法在这个迷宫中给出一个起始点，然后访问一个先前未访问的相邻空间，在这个过程中“挖出”任何走廊空间。然后它在一个以前未访问过的相邻空间上递归调用自身。如果所有相邻空间都已经被访问过，算法就会陷入死胡同，并回溯到先前访问过的空间以访问它的未访问的邻居。当算法回溯到起始位置时，程序结束。

通过运行迷宫生成器程序，您可以看到这个算法的运行过程。当迷宫被挖出时，它会使用@字符显示当前的 x，y 坐标。这个过程看起来像图 11-1。请注意，右上角的第五张图在到达死胡同后回溯到了一个先前的空间，以探索从那个空间的新邻居方向。

图 11-1：递归回溯算法“挖出”的迷宫

让我们更详细地看一下代码。

设置迷宫生成器的常量

迷宫生成器使用了几个常量，我们可以在运行程序之前更改这些常量以改变迷宫的大小和外观。这些常量的 Python 代码如下：

Python

import random

WIDTH = 39 # Width of the maze (must be odd).
HEIGHT = 19 # Height of the maze (must be odd).
assert WIDTH % 2 == 1 and WIDTH >= 3
assert HEIGHT % 2 == 1 and HEIGHT >= 3
SEED = 1
random.seed(SEED)

JavaScript 代码如下：

JavaScript

<script type="text/javascript">

const WIDTH = 39; // Width of the maze (must be odd).
const HEIGHT = 19; // Height of the maze (must be odd).
console.assert(WIDTH % 2 == 1 && WIDTH >= 3);
console.assert(HEIGHT % 2 == 1 && HEIGHT >= 3);

常量WIDTH和HEIGHT决定了迷宫的大小。它们必须是奇数，因为我们的迷宫数据结构要求迷宫的访问空间之间有墙壁，留下奇数维度。为了确保WIDTH和HEIGHT常量被正确设置，我们使用断言来阻止程序如果常量不是奇数或太小的话。

程序依赖于一个随机种子值来根据相同的种子值重现相同的迷宫。这个程序的 Python 版本让我们通过调用random.seed()函数来设置这个值。不幸的是，JavaScript 没有一种明确设置种子值的方法，每次运行程序都会生成不同的迷宫。

Python 代码继续设置一些常量：

Python

# Use these characters for displaying the maze:
EMPTY = ' '
MARK = '@'
WALL = chr(9608) # Character 9608 is '█'
NORTH, SOUTH, EAST, WEST = 'n', 's', 'e', 'w'

这些常量的 JavaScript 代码如下：

JavaScript

// Use these characters for displaying the maze:
const EMPTY = " ";
const MARK = "@";
const WALL = "█"; // Character 9608 is ′█′
const [NORTH, SOUTH, EAST, WEST] = ["n", "s", "e", "w"];

EMPTY和WALL常量影响了迷宫在屏幕上的显示方式。MARK常量用于指出算法在迷宫中的位置。NORTH，SOUTH，EAST和WEST常量表示标记可以通过迷宫的方向，并用于使代码更易读。

创建迷宫数据结构

迷宫数据结构是一个 Python 字典或 JavaScript 对象，它的键是 Python 元组或 JavaScript 数组，表示迷宫中每个空间的 x，y 坐标。这些键的值是WALL或EMPTY常量的字符串。这个字符串表示这个空间是迷宫中的阻挡墙还是可通过的空白空间。

例如，图 11-2 中的迷宫由以下数据结构表示：

{(0, 0): '█', (0, 1): '█', (0, 2): '█', (0, 3): '█', (0, 4): '█', 
(0, 5): '█', (0, 6): '█', (1, 0): '█', (1, 1): ' ', (1, 2): ' ', 
(1, 3): ' ', (1, 4): ' ', (1, 5): ' ', (1, 6): '█', (2, 0): '█', 
(2, 1): '█', (2, 2): '█', (2, 3): '█', (2, 4): '█', (2, 5): ' ', 
(2, 6): '█', (3, 0): '█', (3, 1): ' ', (3, 2): '█', (3, 3): ' ', 
(3, 4): ' ', (3, 5): ' ', (3, 6): '█', (4, 0): '█', (4, 1): ' ', 
(4, 2): '█', (4, 3): ' ', (4, 4): '█', (4, 5): '█', (4, 6): '█', 
(5, 0): '█', (5, 1): ' ', (5, 2): ' ', (5, 3): ' ', (5, 4): ' ', 
(5, 5): ' ', (5, 6): '█', (6, 0): '█', (6, 1): '█', (6, 2): '█', 
(6, 3): '█', (6, 4): '█', (6, 5): '█', (6, 6): '█'}

图 11-2：一个可以用数据结构表示的示例迷宫

程序必须从每个空间设置为WALL开始。然后递归的visit()函数通过将空间设置为EMPTY来挖出迷宫的走廊和交叉点：

Python

# Create the filled-in maze data structure to start:
maze = {}
for x in range(WIDTH):
    for y in range(HEIGHT):
        maze[(x, y)] = WALL # Every space is a wall at first.

相应的 JavaScript 代码如下：

JavaScript

// Create the filled-in maze data structure to start:
let maze = {};
for (let x = 0; x < WIDTH; x++) {
    for (let y = 0; y < HEIGHT; y++) {
        maze[[x, y]] = WALL; // Every space is a wall at first.
    }
}

我们在maze全局变量中创建空字典（在 Python 中）或对象（在 JavaScript 中）。for循环遍历每个可能的 x，y 坐标，将每个设置为WALL，以创建一个完全填充的迷宫。调用visit()将从这个数据结构中刻出迷宫的走廊，将其中的空间设置为EMPTY。

打印迷宫数据结构

为了表示迷宫作为数据结构，Python 程序使用字典，JavaScript 程序使用对象。在这个结构中，键是包含两个整数的列表或数组，分别代表 x 和 y 坐标，而值要么是WALL要么是EMPTY单字符字符串。因此，我们可以在 Python 代码中通过maze[(x, y)]或在 JavaScript 代码中通过maze[[x, y]]访问迷宫中坐标 x，y 的墙壁或空走廊空间。

printMaze()的 Python 代码如下开始：

Python

def printMaze(maze, markX=None, markY=None):
    """Displays the maze data structure in the maze argument. The
    markX and markY arguments are coordinates of the current
    '@' location of the algorithm as it generates the maze."""

    for y in range(HEIGHT):
        for x in range(WIDTH):

printMaze()的 JavaScript 代码如下开始：

JavaScript

function printMaze(maze, markX, markY) {
    // Displays the maze data structure in the maze argument. The
    // markX and markY arguments are coordinates of the current
    // '@' location of the algorithm as it generates the maze.
    document.write('');
 for (let y = 0; y < HEIGHT; y++) {
        for (let x = 0; x < WIDTH; x++) {

printMaze()函数在屏幕上打印作为迷宫参数传递的迷宫数据结构。可选地，如果传递了markX和markY整数参数，则在打印的迷宫中，MARK常量（我们设置为@）将出现在这些 x，y 坐标上。为了确保迷宫以等宽字体打印，JavaScript 版本在打印迷宫本身之前写入 HTML 标签。没有这个 HTML 标签，迷宫将在浏览器中显示扭曲。

在函数内部，嵌套的for循环遍历迷宫数据结构中的每个空间。这些for循环分别从0到HEIGHT的 y 坐标和从0到WIDTH的 x 坐标进行迭代。

在内部的for循环中，如果当前的 x，y 坐标与标记的位置（算法当前正在刻划的位置）匹配，程序会在MARK常量中显示@。Python 代码如下：

Python

 if markX == x and markY == y:
                # Display the '@' mark here:
                print(MARK, end='')
            else:
                # Display the wall or empty space:
                print(maze[(x, y)], end='')

        print() # Print a newline after printing the row.

JavaScript 代码如下：

JavaScript

 if (markX === x && markY === y) {
                // Display the ′@′ mark here:
                document.write(MARK);
            } else {
                // Display the wall or empty space:
                document.write(maze[[x, y]]);
            }
        }
        document.write('
'); // Print a newline after printing the row.
    }
    document.write('');
}

否则，程序通过在maze数据结构中打印maze[(x, y)]（在 Python 中）或maze[[x, y]]（在 JavaScript 中）来显示WALL或EMPTY常量的字符。在内部的for循环完成对 x 坐标的迭代后，我们在行末打印一个换行符，为下一行做准备。

使用递归回溯算法

visit()函数实现了递归回溯算法。该函数有一个列表（在 Python 中）或数组（在 JavaScript 中），用于跟踪先前的visit()函数调用已经访问过的 x，y 坐标。它还就地修改了存储迷宫数据结构的全局maze变量。visit()的 Python 代码如下开始：

Python

def visit(x, y):
    """"Carve out" empty spaces in the maze at x, y and then
    recursively move to neighboring unvisited spaces. This
    function backtracks when the mark has reached a dead end."""
    maze[(x, y)] = EMPTY # "Carve out" the space at x, y.
    printMaze(maze, x, y) # Display the maze as we generate it.
    print('\n\n')

visit()的 JavaScript 代码如下开始：

JavaScript

function visit(x, y) {
    // "Carve out" empty spaces in the maze at x, y and then
    // recursively move to neighboring unvisited spaces. This
    // function backtracks when the mark has reached a dead end.

    maze[[x, y]] = EMPTY; // "Carve out" the space at x, y.
    printMaze(maze, x, y); // Display the maze as we generate it.
    document.write('


');

visit()函数接受 x，y 坐标作为迷宫中算法正在访问的位置的参数。然后函数将maze中这个位置的数据结构更改为空格。为了让用户看到迷宫生成的进展，它调用printMaze()，将x和y参数作为标记的当前位置传递进去。

接下来，递归回溯调用visit()，使用先前未访问的相邻空间的坐标。Python 代码继续如下：

Python

 while True:
        # Check which neighboring spaces adjacent to
        # the mark have not been visited already:
        unvisitedNeighbors = []
        if y > 1 and (x, y - 2) not in hasVisited:
            unvisitedNeighbors.append(NORTH)

        if y < HEIGHT - 2 and (x, y + 2) not in hasVisited:
            unvisitedNeighbors.append(SOUTH)

        if x > 1 and (x - 2, y) not in hasVisited:
            unvisitedNeighbors.append(WEST)

        if x < WIDTH - 2 and (x + 2, y) not in hasVisited:
            unvisitedNeighbors.append(EAST)

JavaScript 代码继续如下：

 while (true) {
        // Check which neighboring spaces adjacent to
        // the mark have not been visited already:
        let unvisitedNeighbors = [];
        if (y > 1 && !JSON.stringify(hasVisited).includes(JSON.stringify([x, y - 2]))) {
            unvisitedNeighbors.push(NORTH);
        }
        if (y < HEIGHT - 2 && !JSON.stringify(hasVisited).includes(JSON.stringify([x, y + 2]))) {
            unvisitedNeighbors.push(SOUTH);
        }
        if (x > 1 && !JSON.stringify(hasVisited).includes(JSON.stringify([x - 2, y]))) {
            unvisitedNeighbors.push(WEST);
        }
        if (x < WIDTH - 2 && !JSON.stringify(hasVisited).includes(JSON.stringify([x + 2, y]))) {
            unvisitedNeighbors.push(EAST);
        }

while循环会继续循环，只要迷宫中这个位置还有未访问的相邻空间。我们在unvisitedNeighbors变量中创建一个未访问的相邻空间的列表或数组。四个if语句检查当前的 x，y 位置是否不在迷宫的边界上（这样我们仍然有相邻的空间要检查），以及相邻空间的 x，y 坐标是否已经出现在hasVisited列表或数组中。

如果所有相邻空间都已经被访问，函数将返回，以便可以回溯到较早的空间。Python 代码继续检查基本情况：

Python

 if len(unvisitedNeighbors) == 0:
            # BASE CASE
            # All neighboring spaces have been visited, so this is a
            # dead end. Backtrack to an earlier space:
            return

JavaScript 代码如下所示：

JavaScript

 if (unvisitedNeighbors.length === 0) {
            // BASE CASE
            // All neighboring spaces have been visited, so this is a
            // dead end. Backtrack to an earlier space:
            return;

递归回溯算法的基本情况是当没有未访问的相邻空间时发生。在这种情况下，函数简单地返回。visit()函数本身没有返回值。相反，递归函数调用visit()以副作用的方式修改全局maze变量中的迷宫数据结构。当对maze()的原始函数调用返回时，maze全局变量包含完全生成的迷宫。

Python 代码继续到这样的递归情况：

Python

 else:
            # RECURSIVE CASE
            # Randomly pick an unvisited neighbor to visit:
            nextIntersection = random.choice(unvisitedNeighbors)

            # Move the mark to an unvisited neighboring space:

            if nextIntersection == NORTH:
                nextX = x
                nextY = y - 2
                maze[(x, y - 1)] = EMPTY # Connecting hallway.
            elif nextIntersection == SOUTH:
                nextX = x
                nextY = y + 2
                maze[(x, y + 1)] = EMPTY # Connecting hallway.
            elif nextIntersection == WEST:
                nextX = x - 2
                nextY = y
                maze[(x - 1, y)] = EMPTY # Connecting hallway.
            elif nextIntersection == EAST:
                nextX = x + 2
                nextY = y
                maze[(x + 1, y)] = EMPTY # Connecting hallway.

            hasVisited.append((nextX, nextY)) # Mark space as visited.
            visit(nextX, nextY) # Recursively visit this space.

JavaScript 代码如下继续：

JavaScript

 } else {
            // RECURSIVE CASE
            // Randomly pick an unvisited neighbor to visit:
            let nextIntersection = unvisitedNeighbors[
            Math.floor(Math.random() * unvisitedNeighbors.length)];

            // Move the mark to an unvisited neighboring space:
            let nextX, nextY;
            if (nextIntersection === NORTH) {
                nextX = x;
                nextY = y - 2;
                maze[[x, y - 1]] = EMPTY; // Connecting hallway.
            } else if (nextIntersection === SOUTH) {
                nextX = x;
                nextY = y + 2;
                maze[[x, y + 1]] = EMPTY; // Connecting hallway.
            } else if (nextIntersection === WEST) {
                nextX = x - 2;
                nextY = y;
                maze[[x - 1, y]] = EMPTY; // Connecting hallway.
            } else if (nextIntersection === EAST) {
                nextX = x + 2;
                nextY = y;
 maze[[x + 1, y]] = EMPTY;    // Connecting hallway.
            }
            hasVisited.push([nextX, nextY]); // Mark space as visited.
            visit(nextX, nextY);             // Recursively visit this space.
        }
    }
}

unvisitedNeighbors列表或数组包含一个或多个NORTH、SOUTH、WEST和EAST常量。我们选择其中一个方向作为下一个递归调用visit()的方向，然后使用这个方向的相邻空间的坐标设置nextX和nextY变量。

之后，我们将nextX和nextY的 x、y 坐标添加到hasVisited列表或数组中，然后对这个相邻空间进行递归调用。这样，visit()函数将继续访问相邻空间，通过将maze中的位置设置为EMPTY来 carve out 迷宫走廊。当前空间和相邻空间之间的连接走廊也被设置为EMPTY。

当没有相邻空间存在时，基本情况简单地返回到较早的位置。在visit()函数中，执行跳回到while循环的开始。while循环中的代码再次检查哪些相邻空间尚未被访问，并对其中一个进行递归visit()调用，或者如果所有相邻空间已经被访问，则返回。

随着迷宫填满走廊并且每个空间都被访问，递归调用将继续返回，直到原始的visit()函数调用返回。此时，迷宫变量包含完全生成的迷宫。

开始递归调用链

递归visit()使用两个全局变量，maze和hasVisited。hasVisited变量是一个包含算法访问过的每个空间的 x、y 坐标的列表或数组，并且从(1, 1)开始，因为那是迷宫的起点。这在 Python 代码中如下：

Python

# Carve out the paths in the maze data structure:
hasVisited = [(1, 1)] # Start by visiting the top-left corner.
visit(1, 1)

# Display the final resulting maze data structure:
printMaze(maze)

这个 JavaScript 代码如下：

JavaScript

// Carve out the paths in the maze data structure:
let hasVisited = [[1, 1]]; // Start by visiting the top-left corner.
visit(1, 1);

// Display the final resulting maze data structure:
printMaze(maze);

在设置hasVisited以包括 1, 1 的 x、y 坐标（迷宫的左上角）之后，我们使用这些坐标调用visit()。这个函数调用将导致生成迷宫走廊的所有递归函数调用。当这个函数调用返回时，hasVisited将包含迷宫的每个 x、y 坐标，而maze将包含完全生成的迷宫。

总结

正如你刚学到的，我们不仅可以使用递归来解决迷宫问题（通过遍历它们作为树数据结构），还可以使用递归回溯算法来生成迷宫。该算法在迷宫中“carves out”走廊，在遇到死胡同时回溯到较早的点。一旦算法被迫回溯到起点，迷宫就完全生成了。

我们可以将没有循环的良好连接的迷宫表示为 DAG——即树数据结构。递归回溯算法利用了递归算法适用于涉及树状数据结构和回溯的问题的思想。

进一步阅读

维基百科通常有关于迷宫生成的条目，其中包括关于递归回溯算法的部分，网址为en.wikipedia.org/wiki/Maze_generation_algorithm#Recursive_backtracker。我创建了一个基于浏览器的递归回溯算法的动画，展示了走廊的“雕刻”过程，网址为scratch.mit.edu/projects/17358777。

如果你对迷宫生成感兴趣，你应该阅读 Jamis Buck 的《程序员的迷宫：编写自己的曲折小通道》（Pragmatic Bookshelf，2015）。

十二、滑动瓷砖求解器

原文：Chapter 12 - Sliding-Tile Solver

译者：飞龙

协议：CC BY-NC-SA 4.0

滑动瓷砖拼图，或15 拼图，是一个小拼图游戏，由一个 4×4 棋盘上的 15 个编号滑动瓷砖组成。一个瓷砖是缺失的，允许相邻的瓷砖滑入棋盘上的空白空间。玩家的目标是将瓷砖移动到数字顺序，就像图 12-1 中一样。这个游戏的一些版本在瓷砖上有一个图片的碎片，当拼图完成时可以组成一个完整的图像。

图 12-1：从数字滑动瓷砖拼图的混乱状态（左）到解决的有序状态（右）的解决方案

顺便说一句，数学家已经证明，即使最难的 15 拼图也可以在 80 步内解决。

递归解决 15 拼图

解决 15 拼图的算法类似于解决迷宫的算法。棋盘的每个状态（即，瓷砖的一种排列）都可以被看作是一个迷宫交叉口，有四条走廊可以通向。在 15 拼图的情况下，将瓷砖沿着四个方向滑动就像选择一个走廊，通向下一个交叉口。

就像你可以将迷宫转化为 DAG 一样，你也可以将 15 拼图转化为树图，就像图 12-2 一样。棋盘状态是节点，最多有四条边（代表滑动瓷砖的方向）通向其他节点（代表结果状态）。根节点是 15 拼图的起始状态。解决状态节点是瓷砖正确排列的状态。从根节点到解决状态的路径详细说明了解决拼图所需的滑动。

图 12-2：解决 15 拼图的任务可以表示为一个图，其中瓷砖状态为节点，滑动为边。

有一些聪明的算法可以解决 15 拼图，但我们也可以递归地探索整个树图，直到找到从根节点到解决节点的路径。这个拼图的树可以用深度优先搜索（DFS）算法进行搜索。然而，与连接良好的迷宫不同，15 拼图的树图不是 DAG。相反，图的节点是无向的，因为你可以通过撤消之前做的滑动来遍历边的两个方向。

图 12-3 显示了两个节点之间的无向边的示例。因为可以在这两个节点之间来回移动，我们的 15 拼图算法在找到解决方案之前可能会遇到堆栈溢出。

图 12-3：15 拼图的节点之间有无向边（没有箭头头）因为滑动可以通过执行相反的滑动来撤消。

为了优化我们的算法，我们将避免撤销上一次滑动的滑动。然而，仅凭这种优化无法使算法免受堆栈溢出的影响。虽然它使树图中的边缘变得有向，但它并不会将拼图求解算法转变为 DAG，因为它具有从较低节点到较高节点的循环或循环。如果您以循环模式滑动瓷砖，就会发生这些循环，如图 12-4 所示。

图 12-4：15 拼图图中循环的一个例子

图中的循环意味着底部的后续节点可能会回到顶部的节点。我们的求解算法可能会在这个循环中“卡住”，永远不会探索具有实际解决方案的分支。在实践中，这个无限循环会导致堆栈溢出。

我们仍然可以使用递归来解决 15 拼图。我们只需要为最大移动次数添加自己的基本情况，以避免导致堆栈溢出。然后，当达到最大滑动次数时，算法将开始回溯到较早的节点。如果 15 拼图求解器项目无法在 10 次滑动的所有可能组合中找到解决方案，它将尝试使用最多 11 次滑动。如果拼图在 11 次移动中无法解决，项目将尝试 12 次移动，依此类推。这可以防止算法陷入探索无限循环移动而不是探索较少移动可能解决方案的困境。

完整的滑动瓷砖求解程序

让我们首先看一下滑动瓷砖拼图求解程序的完整源代码。本章的其余部分将逐个解释代码的每个部分。

将代码的 Python 版本复制到名为slidingTileSolver.py的文件中：

Python

import random, time

DIFFICULTY = 40 # How many random slides a puzzle starts with.
SIZE = 4 # The board is SIZE x SIZE spaces.
random.seed(1) # Select which puzzle to solve.

BLANK = 0
UP = 'up'
DOWN = 'down'
LEFT = 'left'
RIGHT = 'right'

def displayBoard(board):
    """Display the tiles stored in `board` on the screen."""
    for y in range(SIZE): # Iterate over each row.
        for x in range(SIZE): # Iterate over each column.
            if board[y * SIZE + x] == BLANK:
                print('__ ', end='') # Display blank tile.
            else:
                print(str(board[y * SIZE + x]).rjust(2) + ' ', end='')
        print() # Print a newline at the end of the row.

def getNewBoard():
    """Return a list that represents a new tile puzzle."""
    board = []
    for i in range(1, SIZE * SIZE):
        board.append(i)
    board.append(BLANK)
    return board

def findBlankSpace(board):
    """Return an [x, y] list of the blank space's location."""
    for x in range(SIZE):
 for y in range(SIZE):
            if board[y * SIZE + x] == BLANK:
                return [x, y]

def makeMove(board, move):
    """Modify `board` in place to carry out the slide in `move`."""
    bx, by = findBlankSpace(board)
    blankIndex = by * SIZE + bx

    if move == UP:
        tileIndex = (by + 1) * SIZE + bx
    elif move == LEFT:
        tileIndex = by * SIZE + (bx + 1)
    elif move == DOWN:
        tileIndex = (by - 1) * SIZE + bx
    elif move == RIGHT:
        tileIndex = by * SIZE + (bx - 1)

    # Swap the tiles at blankIndex and tileIndex:
    board[blankIndex], board[tileIndex] = board[tileIndex], board[blankIndex]

def undoMove(board, move):
    """Do the opposite move of `move` to undo it on `board`."""
    if move == UP:
        makeMove(board, DOWN)
    elif move == DOWN:
        makeMove(board, UP)
    elif move == LEFT:
        makeMove(board, RIGHT)
    elif move == RIGHT:
        makeMove(board, LEFT)

def getValidMoves(board, prevMove=None):
    """Returns a list of the valid moves to make on this board. If
    prevMove is provided, do not include the move that would undo it."""

    blankx, blanky = findBlankSpace(board)

    validMoves = []
    if blanky != SIZE - 1 and prevMove != DOWN:
        # Blank space is not on the bottom row.
        validMoves.append(UP)

    if blankx != SIZE - 1 and prevMove != RIGHT:
        # Blank space is not on the right column.
        validMoves.append(LEFT)

    if blanky != 0 and prevMove != UP:
        # Blank space is not on the top row.
        validMoves.append(DOWN)

 if blankx != 0 and prevMove != LEFT:
        # Blank space is not on the left column.
        validMoves.append(RIGHT)

    return validMoves

def getNewPuzzle():
    """Get a new puzzle by making random slides from the solved state."""
    board = getNewBoard()
    for i in range(DIFFICULTY):
        validMoves = getValidMoves(board)
        makeMove(board, random.choice(validMoves))
    return board

def solve(board, maxMoves):
    """Attempt to solve the puzzle in `board` in at most `maxMoves`
    moves. Returns True if solved, otherwise False."""
    print('Attempting to solve in at most', maxMoves, 'moves...')
    solutionMoves = [] # A list of UP, DOWN, LEFT, RIGHT values.
    solved = attemptMove(board, solutionMoves, maxMoves, None)

    if solved:
        displayBoard(board)
        for move in solutionMoves:
            print('Move', move)
            makeMove(board, move)
            print() # Print a newline.
            displayBoard(board)
            print() # Print a newline.

        print('Solved in', len(solutionMoves), 'moves:')
        print(', '.join(solutionMoves))
        return True # Puzzle was solved.
    else:
        return False # Unable to solve in maxMoves moves.

def attemptMove(board, movesMade, movesRemaining, prevMove):
    """A recursive function that attempts all possible moves on `board`
    until it finds a solution or reaches the `maxMoves` limit.
    Returns True if a solution was found, in which case `movesMade`
    contains the series of moves to solve the puzzle. Returns False
    if `movesRemaining` is less than 0."""

    if movesRemaining < 0:
        # BASE CASE - Ran out of moves.
        return False

    if board == SOLVED_BOARD:
        # BASE CASE - Solved the puzzle.
        return True

    # RECURSIVE CASE - Attempt each of the valid moves:
 for move in getValidMoves(board, prevMove):
        # Make the move:
        makeMove(board, move)
        movesMade.append(move)

        if attemptMove(board, movesMade, movesRemaining - 1, move):
            # If the puzzle is solved, return True:
            undoMove(board, move) # Reset to the original puzzle.
            return True

        # Undo the move to set up for the next move:
        undoMove(board, move)
        movesMade.pop() # Remove the last move since it was undone.
    return False # BASE CASE - Unable to find a solution.

# Start the program:
SOLVED_BOARD = getNewBoard()
puzzleBoard = getNewPuzzle()
displayBoard(puzzleBoard)
startTime = time.time()

maxMoves = 10
while True:
    if solve(puzzleBoard, maxMoves):
        break # Break out of the loop when a solution is found.
    maxMoves += 1
print('Run in', round(time.time() - startTime, 3), 'seconds.')

将代码的 JavaScript 版本复制到名为slidingTileSolver.html的文件中：

<script type="text/javascript">
const DIFFICULTY = 40; // How many random slides a puzzle starts with.
const SIZE = 4; // The board is SIZE x SIZE spaces.

const BLANK = 0;
const UP = "up";
const DOWN = "down";
const LEFT = "left";
const RIGHT = "right";

function displayBoard(board) {
    // Display the tiles stored in `board` on the screen.
    document.write("
");
    for (let y = 0; y < SIZE; y++) { // Iterate over each row.
        for (let x = 0; x < SIZE; x++) { // Iterate over each column.
            if (board[y * SIZE + x] == BLANK) {
                document.write('__ '); // Display blank tile.
            } else {
                document.write(board[y * SIZE + x].toString().padStart(2) + " ");
            }
        }
 document.write("
"); // Print a newline at the end of the row.
    }
    document.write("
");
}

function getNewBoard() {
    // Return a list that represents a new tile puzzle.
    let board = [];
    for (let i = 1; i < SIZE * SIZE; i++) {
        board.push(i);
    }
    board.push(BLANK);
    return board;
}

function findBlankSpace(board) {
    // Return an [x, y] array of the blank space's location.
    for (let x = 0; x < SIZE; x++) {
        for (let y = 0; y < SIZE; y++) {
            if (board[y * SIZE + x] === BLANK) {
                return [x, y];
            }
        }
    }
}

function makeMove(board, move) {
    // Modify `board` in place to carry out the slide in `move`.
    let bx, by;
    [bx, by] = findBlankSpace(board);
    let blankIndex = by * SIZE + bx;

    let tileIndex;
    if (move === UP) {
        tileIndex = (by + 1) * SIZE + bx;
    } else if (move === LEFT) {
        tileIndex = by * SIZE + (bx + 1);
    } else if (move === DOWN) {
        tileIndex = (by - 1) * SIZE + bx;
    } else if (move === RIGHT) {
        tileIndex = by * SIZE + (bx - 1);
    }

    // Swap the tiles at blankIndex and tileIndex:
    [board[blankIndex], board[tileIndex]] = [board[tileIndex], board[blankIndex]];
}

function undoMove(board, move) {
    // Do the opposite move of `move` to undo it on `board`.
 if (move === UP) {
        makeMove(board, DOWN);
    } else if (move === DOWN) {
        makeMove(board, UP);
    } else if (move === LEFT) {
        makeMove(board, RIGHT);
    } else if (move === RIGHT) {
        makeMove(board, LEFT);
    }
}

function getValidMoves(board, prevMove) {
    // Returns a list of the valid moves to make on this board. If
    // prevMove is provided, do not include the move that would undo it.

    let blankx, blanky;
    [blankx, blanky] = findBlankSpace(board);

    let validMoves = [];
    if (blanky != SIZE - 1 && prevMove != DOWN) {
        // Blank space is not on the bottom row.
        validMoves.push(UP);
    }
    if (blankx != SIZE - 1 && prevMove != RIGHT) {
        // Blank space is not on the right column.
        validMoves.push(LEFT);
    }
    if (blanky != 0 && prevMove != UP) {
        // Blank space is not on the top row.
        validMoves.push(DOWN);
    }
    if (blankx != 0 && prevMove != LEFT) {
        // Blank space is not on the left column.
        validMoves.push(RIGHT);
    }
    return validMoves;
}

function getNewPuzzle() {
    // Get a new puzzle by making random slides from the solved state.
    let board = getNewBoard();
    for (let i = 0; i < DIFFICULTY; i++) {
        let validMoves = getValidMoves(board);
        makeMove(board, validMoves[Math.floor(Math.random() * validMoves.length)]);
    }
    return board;
}

function solve(board, maxMoves) {
    // Attempt to solve the puzzle in `board` in at most `maxMoves`
    // moves. Returns true if solved, otherwise false.
    document.write("Attempting to solve in at most " + maxMoves + " moves...
");
    let solutionMoves = []; // A list of UP, DOWN, LEFT, RIGHT values.
 let solved = attemptMove(board, solutionMoves, maxMoves, null);

    if (solved) {
        displayBoard(board);
        for (let move of solutionMoves) {
            document.write("Move " + move + "
");
            makeMove(board, move);
            document.write("
"); // Print a newline.
            displayBoard(board);
            document.write("
"); // Print a newline.
        }
        document.write("Solved in " + solutionMoves.length + " moves:
");
        document.write(solutionMoves.join(", ") + "
");
        return true; // Puzzle was solved.
    } else {
        return false; // Unable to solve in maxMoves moves.
    }
}

function attemptMove(board, movesMade, movesRemaining, prevMove) {
    // A recursive function that attempts all possible moves on `board`
    // until it finds a solution or reaches the `maxMoves` limit.
    // Returns true if a solution was found, in which case `movesMade`
    // contains the series of moves to solve the puzzle. Returns false
    // if `movesRemaining` is less than 0.

    if (movesRemaining < 0) {
        // BASE CASE - Ran out of moves.
        return false;
    }

    if (JSON.stringify(board) == SOLVED_BOARD) {
        // BASE CASE - Solved the puzzle.
        return true;
    }

    // RECURSIVE CASE - Attempt each of the valid moves:
    for (let move of getValidMoves(board, prevMove)) {
        // Make the move:
        makeMove(board, move);
        movesMade.push(move);

        if (attemptMove(board, movesMade, movesRemaining - 1, move)) {
            // If the puzzle is solved, return true:
            undoMove(board, move); // Reset to the original puzzle.
            return true;
        }

        // Undo the move to set up for the next move:
        undoMove(board, move);
        movesMade.pop(); // Remove the last move since it was undone.
    }
    return false; // BASE CASE - Unable to find a solution.
}
 // Start the program:
const SOLVED_BOARD = JSON.stringify(getNewBoard());
let puzzleBoard = getNewPuzzle();
displayBoard(puzzleBoard);
let startTime = Date.now();

let maxMoves = 10;
while (true) {
    if (solve(puzzleBoard, maxMoves)) {
        break; // Break out of the loop when a solution is found.
    }
    maxMoves += 1;
}
document.write("Run in " + Math.round((Date.now() - startTime) / 100) / 10 + " seconds.
");
</script>

程序的输出如下所示：

 7  1  3  4
 2  5 10  8
__  6  9 11
13 14 15 12
Attempting to solve in at most 10 moves...
Attempting to solve in at most 11 moves...
Attempting to solve in at most 12 moves...
# --snip--
 1  2  3  4
 5  6  7  8
 9 10 11 __
13 14 15 12

Move up

 1  2  3  4
 5  6  7  8
 9 10 11 12
13 14 15 __

Solved in 18 moves:
left, down, right, down, left, up, right, up, left, left, down, 
right, right, up, left, left, left, up
Run in 39.519 seconds.

请注意，当 JavaScript 在浏览器中运行时，代码必须在显示任何输出之前完成。在那之前，它可能会看起来已经冻结，您的浏览器可能会询问您是否想要提前停止它。您可以忽略这个警告，让程序继续工作，直到解决了拼图。

程序的递归attemptMove()函数通过尝试每种可能的滑动组合来解决滑动瓷砖拼图。该函数给出一个要尝试的移动。如果这解决了拼图，函数将返回一个布尔值True。否则，它将调用attemptMove()以及它可以进行的所有其他可能移动，并在超过最大移动次数之前找不到解决方案时返回一个布尔值False。我们稍后将更详细地探讨这个函数。

我们用来表示滑动瓷砖板的数据结构是一个整数列表（在 Python 中）或数组（在 JavaScript 中），其中0表示空白空间。在我们的程序中，这个数据结构通常存储在一个名为board的变量中。board[y * SIZE + x]处的值与板上坐标 x，y 处的瓷砖匹配，如图 12-5 所示。例如，如果SIZE常量为4，则在坐标 3, 1 处的值可以在board[1 * 4 + 3]找到。

这个小计算使我们能够使用一维数组或列表来存储二维瓷砖板的值。这种编程技术不仅在我们的项目中有用，而且对于任何必须存储在数组或列表中的二维数据结构都很有用，比如以字节流存储的二维图像。

图 12-5：板上每个空间的 x、y 坐标（左）和相应的数据结构索引（右）

让我们来看一些示例数据结构。之前在图 12-1 的左侧显示的混乱瓷砖的板将被表示为以下内容：

1. [15, 2, 1, 12, 8, 5, 6, 11, 4, 9, 10, 7, 3, 14, 13, 0]

在图 12-1 的右侧，解决的有序拼图将被表示为：

1. [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0]

我们程序中的所有函数都将期望遵循这种格式的板数据结构。

不幸的是，4×4 版本的滑动瓷砖拼图有太多可能的移动，普通笔记本电脑需要数周才能解决。您可以将SIZE常量从4更改为3，以解决一个更简单的 3×3 版本的拼图。完成的、有序的 3×3 拼图的数据结构将如下所示：

1. [1, 2, 3, 4, 5, 6, 7, 8, 0]。

设置程序的常量

在源代码的开头，程序使用一些常量使代码更易读。Python 代码如下：

Python

import random, time

DIFFICULTY = 40 # How many random slides a puzzle starts with.
SIZE = 4 # The board is SIZE x SIZE spaces.
random.seed(1) # Select which puzzle to solve.

BLANK = 0
UP = 'up'
DOWN = 'down'
LEFT = 'left'
RIGHT = 'right'

JavaScript 代码如下：

JavaScript

<script type="text/javascript">
const DIFFICULTY = 40; // How many random slides a puzzle starts with.
const SIZE = 4; // The board is SIZE x SIZE spaces.

const BLANK = 0;
const UP = "up";
const DOWN = "down";
const LEFT = "left";
const RIGHT = "right";

为了获得可重现的随机数，Python 程序将随机数种子设置为1。相同的种子值将始终产生相同的随机拼图，这对于调试很有用。您可以将种子值更改为任何其他整数以创建不同的拼图。JavaScript 没有办法设置其随机种子值，slidingtilesolver.html也没有类似的功能。

SIZE常量设置了方形板的大小。您可以将此大小更改为任何值，但 4×4 板是标准的，而 3×3 板对于测试很有用，因为程序很快就能解决它们。BLANK常量在拼图数据结构中用于表示空白空间，必须保持为0。UP、DOWN、LEFT和RIGHT常量用于使代码可读，类似于第十一章中迷宫生成器项目中的NORTH、SOUTH、WEST和EAST常量。

将滑动瓷砖拼图表示为数据

滑动瓷砖板的数据结构只是一个整数列表或数组。它代表实际拼图板的方式是程序中的函数如何使用它。该程序中的displayBoard()、getNewBoard()、findBlankSpace()和其他函数都处理这个数据结构。

显示板

第一个函数displayBoard()在屏幕上打印板数据结构。displayBoard()函数的 Python 代码如下：

Python

def displayBoard(board):
    """Display the tiles stored in `board` on the screen."""
    for y in range(SIZE): # Iterate over each row.
        for x in range(SIZE): # Iterate over each column.
            if board[y * SIZE + x] == BLANK:
                print('__ ', end='') # Display blank tile.
            else:
                print(str(board[y * SIZE + x]).rjust(2) + ' ', end='')
        print() # Print a newline at the end of the row.

displayBoard()函数的 JavaScript 代码如下：

function displayBoard(board) {
    // Display the tiles stored in `board` on the screen.
    document.write("
");
    for (let y = 0; y < SIZE; y++) { // Iterate over each row.
        for (let x = 0; x < SIZE; x++) { // Iterate over each column.
            if (board[y * SIZE + x] == BLANK) {
                document.write('__ '); // Display blank tile.
            } else {
                document.write(board[y * SIZE + x].toString().padStart(2) + " ");
            }
        }
        document.write("
");
    }
    document.write("
");
}

嵌套的一对for循环遍历板上的每一行和每一列。第一个for循环遍历 y 坐标，第二个for循环遍历 x 坐标。这是因为程序需要在打印换行字符之前打印单行的所有列，以继续下一行。

if语句检查当前 x、y 坐标处的瓷砖是否为空白瓷砖。如果是，程序打印两个下划线并带有一个尾随空格。否则，else块中的代码打印带有尾随空格的瓷砖编号。尾随空格是屏幕上分隔瓷砖编号的内容。如果瓷砖编号是一个数字，rjust()或padStart()方法将插入一个额外的空格，以便瓷砖编号与屏幕上的两位数对齐。

例如，假设左侧的混乱拼图在图 12-1 中由这个数据结构表示：

[15, 2, 1, 12, 8, 5, 6, 11, 4, 9, 10, 7, 3, 14, 13, 0]

当数据结构传递给displayBoard()时，它会打印以下文本：

15  2  1 12 
 8  5  6 11 
 4  9 10  7 
 3 14 13 __

创建一个新的板数据结构

接下来，getNewBoard()函数返回一个新的板数据结构，其中瓷砖放在它们有序的、解决的位置上。getNewBoard()函数的 Python 代码如下：

Python

def getNewBoard():
    """Return a list that represents a new tile puzzle."""
    board = []
    for i in range(1, SIZE * SIZE):
        board.append(i)
    board.append(BLANK)
    return board

getNewBoard()函数的 JavaScript 代码如下：

JavaScript

function getNewBoard() {
    // Return a list that represents a new tile puzzle.
    let board = [];
    for (let i = 1; i < SIZE * SIZE; i++) {
        board.push(i);
    }
    board.push(BLANK);
    return board;
}

getNewBoard()函数返回适合于SIZE常量（3×3 或 4×4）中的整数的板数据结构。for循环生成这个列表或数组，其中包含从1到SIZE的平方，最后一个是0（存储在BLANK常量中的值），表示右下角的空白空间。

找到空白空间的坐标

我们的程序使用findBlankSpace()函数来找到板上空白空间的 x、y 坐标。Python 代码如下：

Python

def findBlankSpace(board):
    """Return an [x, y] list of the blank space's location."""
    for x in range(SIZE):
        for y in range(SIZE):
            if board[y * SIZE + x] == BLANK:
                return [x, y]

JavaScript 代码如下：

JavaScript

function findBlankSpace(board) {
    // Return an [x, y] array of the blank space's location.
    for (let x = 0; x < SIZE; x++) {
        for (let y = 0; y < SIZE; y++) {
            if (board[y * SIZE + x] === BLANK) {
                return [x, y];
            }
        }
    }
}

像displayBoard()函数一样，findBlankSpace()函数有一对嵌套的for循环。这些for循环将循环遍历板数据结构中的每个位置。当board[y * SIZE + x]代码找到空白空间时，它会以 Python 列表或 JavaScript 数组中的两个整数的形式返回 x 和 y 坐标。

进行移动

接下来，makeMove()函数接受两个参数：一个板数据结构和一个UP、DOWN、LEFT或RIGHT方向，用于在该板上滑动一个瓷砖。这段代码相当重复，所以使用bx和by这样的简短变量名来表示空白空间的 x 和 y 坐标。

为了进行移动，板数据结构交换了移动瓷砖的值与空白瓷砖的0的值。makeMove()函数的 Python 代码如下：

Python

def makeMove(board, move):
    """Modify `board` in place to carry out the slide in `move`."""
    bx, by = findBlankSpace(board)
    blankIndex = by * SIZE + bx

    if move == UP:
        tileIndex = (by + 1) * SIZE + bx
    elif move == LEFT:
        tileIndex = by * SIZE + (bx + 1)
    elif move == DOWN:
        tileIndex = (by - 1) * SIZE + bx
    elif move == RIGHT:
        tileIndex = by * SIZE + (bx - 1)

    # Swap the tiles at blankIndex and tileIndex:
    board[blankIndex], board[tileIndex] = board[tileIndex], board[blankIndex]

makeMove()函数的 JavaScript 代码如下：

function makeMove(board, move) {
    // Modify `board` in place to carry out the slide in `move`.
    let bx, by;
    [bx, by] = findBlankSpace(board);
    let blankIndex = by * SIZE + bx;

 let tileIndex;
    if (move === UP) {
        tileIndex = (by + 1) * SIZE + bx;
    } else if (move === LEFT) {
        tileIndex = by * SIZE + (bx + 1);
    } else if (move === DOWN) {
        tileIndex = (by - 1) * SIZE + bx;
    } else if (move === RIGHT) {
        tileIndex = by * SIZE + (bx - 1);
    }

    // Swap the tiles at blankIndex and tileIndex:
    [board[blankIndex], board[tileIndex]] = [board[tileIndex], board[blankIndex]];
}

if语句根据move参数确定要移动的瓷砖的索引。然后，函数通过交换board[blankindex]处的BLANK值和board[tileIndex]处的编号瓷砖来“滑动”瓷砖。makeMove()函数不返回任何内容。相反，它直接修改了board数据结构。

Python 有a, b = b, a的语法来交换两个变量的值。对于 JavaScript，我们需要将它们包装在一个数组中，比如[a, b] = [b, a]来执行交换。我们在函数的最后使用这种语法来交换board[blankIndex]和board[tileIndex]中的值。

撤消移动

接下来，在递归算法的回溯部分，我们的程序需要撤消移动。这就像在与初始移动相反的方向上进行移动一样简单。undoMove()函数的 Python 代码如下：

Python

def undoMove(board, move):
    """Do the opposite move of `move` to undo it on `board`."""
    if move == UP:
        makeMove(board, DOWN)
    elif move == DOWN:
        makeMove(board, UP)
    elif move == LEFT:
        makeMove(board, RIGHT)
    elif move == RIGHT:
        makeMove(board, LEFT)

undoMove()函数的 JavaScript 代码如下：

JavaScript

function undoMove(board, move) {
    // Do the opposite move of `move` to undo it on `board`.
    if (move === UP) {
        makeMove(board, DOWN);
    } else if (move === DOWN) {
        makeMove(board, UP);
    } else if (move === LEFT) {
        makeMove(board, RIGHT);
 } else if (move === RIGHT) {
        makeMove(board, LEFT);
    }
}

我们已经将交换逻辑编程到makeMove()函数中，所以undoMove()可以调用该函数来执行与move参数相反的方向。这样，通过makeMove(someBoard, someMove)函数调用在一个假设的someBoard数据结构上进行的假设的someMove移动可以通过调用undoMove(someBoard, someMove)来撤消。

设置一个新的谜题

要创建一个新的打乱的拼图，我们不能简单地将方块放在随机位置，因为一些方块的配置会产生无效的、无法解决的拼图。相反，我们需要从一个已解决的拼图开始，然后进行许多随机移动。解决这个拼图就变成了弄清楚哪些滑动可以撤消这些随机滑动，以恢复到原始的有序配置。

但并不总是可以在四个方向中的每个方向上进行移动。例如，如果空白区域在右下角，就像图 12-6 中一样，方块只能向下或向右滑动，因为没有方块可以向左或向上滑动。此外，如果在图 12-6 中向上滑动 7 号方块是上一个移动，那么向下滑动就会被移除作为有效的移动，因为它会撤消上一个移动。

图 12-6：如果空白区域在右下角，向下和向右是唯一有效的滑动方向。

为了帮助我们，我们需要一个getValidMoves()函数，它可以告诉我们在给定的板块数据结构上哪些滑动方向是可能的：

Python

def getValidMoves(board, prevMove=None):
    """Returns a list of the valid moves to make on this board. If
    prevMove is provided, do not include the move that would undo it."""

    blankx, blanky = findBlankSpace(board)

    validMoves = []
 if blanky != SIZE - 1 and prevMove != DOWN:
        # Blank space is not on the bottom row.
        validMoves.append(UP)

    if blankx != SIZE - 1 and prevMove != RIGHT:
        # Blank space is not on the right column.
        validMoves.append(LEFT)

    if blanky != 0 and prevMove != UP:
        # Blank space is not on the top row.
        validMoves.append(DOWN)

    if blankx != 0 and prevMove != LEFT:
        # Blank space is not on the left column.
        validMoves.append(RIGHT)

    return validMoves

这个函数的 JavaScript 代码如下：

JavaScript

function getValidMoves(board, prevMove) {
    // Returns a list of the valid moves to make on this board. If
    // prevMove is provided, do not include the move that would undo it.

    let blankx, blanky;
    [blankx, blanky] = findBlankSpace(board);

    let validMoves = [];
    if (blanky != SIZE - 1 && prevMove != DOWN) {
        // Blank space is not on the bottom row.
        validMoves.push(UP);
    }
    if (blankx != SIZE - 1 && prevMove != RIGHT) {
        // Blank space is not on the right column.
        validMoves.push(LEFT);
    }
    if (blanky != 0 && prevMove != UP) {
        // Blank space is not on the top row.
        validMoves.push(DOWN);
    }
    if (blankx != 0 && prevMove != LEFT) {
        // Blank space is not on the left column.
        validMoves.push(RIGHT);
    }
    return validMoves;
}

getValidMoves()函数的第一件事是调用findBlankSpace()并将空白区域的 x、y 坐标存储在变量blankx和blanky中。接下来，函数使用一个空的 Python 列表或空的 JavaScript 数组设置了validMoves变量，用于保存滑动的所有有效方向。

回顾图 12-5，y 坐标为0表示板块的顶边缘。如果blanky，空白区域的 y 坐标，不是0，那么我们知道空白区域不在顶边缘。如果前一个移动也不是DOWN，那么up就是一个有效的移动，代码会将UP添加到validMoves中。

同样，左边缘的 x 坐标为0，底边缘的 y 坐标为SIZE - 1，右边缘的 x 坐标为SIZE - 1。使用表达式SIZE - 1可以确保这段代码无论板块是 3×3、4×4 还是其他任何尺寸都能正常工作。getValidMoves()函数对所有四个方向进行这些检查，然后返回validMoves。

接下来，getNewPuzzle()函数返回程序要解决的打乱板块的数据结构。不能简单地将方块随机放在板块上，因为一些方块的配置会产生无法解决的拼图。为了避免这种情况，getNewPuzzle()函数从有序的解决板块开始，然后对其应用大量的随机滑动。解决这个拼图实际上就是找出撤消这些滑动的移动。getNewPuzzle()函数的 Python 代码如下：

Python

def getNewPuzzle():
    """Get a new puzzle by making random slides from the solved state."""
    board = getNewBoard()
    for i in range(DIFFICULTY):
        validMoves = getValidMoves(board)
        makeMove(board, random.choice(validMoves))
    return board

JavaScript 代码如下：

function getNewPuzzle() {
    // Get a new puzzle by making random slides from the solved state.
    let board = getNewBoard();
    for (let i = 0; i < DIFFICULTY; i++) {
        let validMoves = getValidMoves(board);
        makeMove(board, validMoves[Math.floor(Math.random() * validMoves.length)]);
    }
    return board;
}

调用getNewBoard()获取了一个有序、解决状态的板块数据结构。for循环调用getValidMoves()来获取给定板块当前状态下的有效移动列表，然后从列表中随机选择一个移动调用makeMove()。无论validMoves列表或数组包含什么组合的UP、DOWN、LEFT和RIGHT值，Python 中的random.choice()函数和 JavaScript 中的Math.floor()和Math.random()函数都会处理从validMoves中进行随机选择。

DIFFICULTY常量确定for循环从makeMove()中应用多少随机滑动。DIFFICULTY中的整数越高，拼图就会变得更加混乱。尽管这会导致一些纯粹偶然地撤销先前的移动的移动，例如向左滑动然后立即向右滑动，但是通过足够的滑动，函数会产生一个彻底混乱的棋盘。为了测试目的，DIFFICULTY设置为40，允许程序在大约一分钟内产生一个解决方案。对于一个更真实的 15 拼图，你应该将DIFFICULTY改为200。

在创建和打乱board棋盘数据结构之后，getNewPuzzle()函数返回它。

递归解决滑动拼图

现在我们已经有了创建和操作拼图数据结构的函数，让我们创建通过递归滑动每个可能方向的拼图解决函数。

attemptMove()函数在一个棋盘数据结构上执行单个滑动，然后递归调用自身，对棋盘可以进行的每个有效移动调用一次。存在多个基本情况。如果棋盘数据结构处于已解状态，则函数返回布尔值True；如果达到了最大移动次数，则返回布尔值False。此外，如果递归调用返回了True，那么attemptMove()应该返回True，如果所有有效移动的递归调用都返回了False，那么attemptMove()应该返回False。

solve()函数

solve()函数接受一个棋盘数据结构和算法在回溯之前应尝试的最大移动次数。然后它执行对attemptMove()的第一次调用。如果这第一次对attemptMove()的调用返回True，那么solve()中的代码会显示解决拼图的一系列步骤。如果返回False，那么solve()中的代码会告诉用户在这个最大移动次数下找不到解决方案。

Python 中的solve()代码开始如下：

Python

def solve(board, maxMoves):
    """Attempt to solve the puzzle in `board` in at most `maxMoves`
    moves. Returns True if solved, otherwise False."""
    print('Attempting to solve in at most', maxMoves, 'moves...')
    solutionMoves = [] # A list of UP, DOWN, LEFT, RIGHT values.
    solved = attemptMove(board, solutionMoves, maxMoves, None)

JavaScript 中的solve()代码开始如下：

function solve(board, maxMoves) {
    // Attempt to solve the puzzle in `board` in at most `maxMoves`
    // moves. Returns true if solved, otherwise false.
    document.write("Attempting to solve in at most " + maxMoves + " moves...
");
    let solutionMoves = []; // A list of UP, DOWN, LEFT, RIGHT values.
    let solved = attemptMove(board, solutionMoves, maxMoves, null);

solve()函数有两个参数：board包含要解决的拼图的数据结构，maxMoves是函数应该尝试的最大移动次数。solutionMoves列表或数组包含产生解决状态的UP、DOWN、LEFT和RIGHT值的序列。attemptMove()函数在进行递归调用时会修改这个列表或数组。如果初始的attemptMove()函数找到解决方案并返回True，solutionMoves包含解决方案的移动序列。

然后solve()函数对attemptMove()进行初始调用，并将其返回的True或False存储在solved变量中。solve()函数的其余部分处理这两种情况：

Python

 if solved:
        displayBoard(board)
        for move in solutionMoves:
            print('Move', move)
            makeMove(board, move)
            print() # Print a newline.
            displayBoard(board)
            print() # Print a newline.

        print('Solved in', len(solutionMoves), 'moves:')
        print(', '.join(solutionMoves))
        return True # Puzzle was solved.
    else:
        return False # Unable to solve in maxMoves moves.

JavaScript 代码如下：

JavaScript

 if (solved) {
        displayBoard(board);
        for (let move of solutionMoves) {
            document.write("Move " + move + "
");
            makeMove(board, move);
            document.write("
"); // Print a newline.
            displayBoard(board);
            document.write("
"); // Print a newline.
        }
        document.write("Solved in " + solutionMoves.length + " moves:
");
        document.write(solutionMoves.join(", ") + "
");
        return true; // Puzzle was solved.
    } else {
        return false; // Unable to solve in maxMoves moves.
    }
}

如果attemptMove()找到解决方案，程序会运行solutionMoves列表或数组中收集的所有移动，并在每次滑动后显示棋盘。这向用户证明了attemptMove()收集的移动是拼图的真正解决方案。最后，solve()函数本身返回True。如果attemptMove()无法找到解决方案，solve()函数会简单地返回False。

attemptMove()函数

让我们来看看attemptMove()，这是我们解决拼图的核心递归函数。记住滑动拼图产生的树图；调用attemptMove()来表示某个方向就像是沿着图的边缘前进到下一个节点。递归的attemptMove()调用会在树中进一步前进。当这个递归的attemptMove()调用返回时，它会回溯到先前的节点。当attemptMove()回溯到根节点时，程序执行已经返回到solve()函数。

Python 代码attemptMove()的开始如下：

Python

def attemptMove(board, movesMade, movesRemaining, prevMove):
    """A recursive function that attempts all possible moves on `board`
    until it finds a solution or reaches the `maxMoves` limit.
    Returns True if a solution was found, in which case `movesMade`
    contains the series of moves to solve the puzzle. Returns False
    if `movesRemaining` is less than 0."""

    if movesRemaining < 0:
        # BASE CASE - Ran out of moves.
        return False

    if board == SOLVED_BOARD:
        # BASE CASE - Solved the puzzle.
        return True

attemptMove()的 JavaScript 代码如下：

JavaScript

function attemptMove(board, movesMade, movesRemaining, prevMove) {
    // A recursive function that attempts all possible moves on `board`
    // until it finds a solution or reaches the `maxMoves` limit.
    // Returns true if a solution was found, in which case `movesMade`
    // contains the series of moves to solve the puzzle. Returns false
    // if `movesRemaining` is less than 0.

    if (movesRemaining < 0) {
        // BASE CASE - Ran out of moves.
        return false;
    }

    if (JSON.stringify(board) == SOLVED_BOARD) {
        // BASE CASE - Solved the puzzle.
        return true;
    }

attemptMove()函数有四个参数。board参数包含要解决的瓷砖拼图板数据结构。movesMade参数包含attemptMove()就地修改的列表或数组，添加了递归算法产生的UP、DOWN、LEFT和RIGHT值。如果attemptMove()解决了拼图，movesMade将包含导致解决方案的移动。这个列表或数组也是solve()函数中的solutionMoves变量所指的。

solve()函数使用其maxMoves变量作为对attemptMove()的初始调用中的movesRemaining参数。每个递归调用传递maxMoves - 1作为maxMoves的下一个值，导致在进行更多递归调用时减少。当它变小于0时，attemptMove()函数停止进行额外的递归调用并返回False。

最后，prevMove参数包含前一次调用attemptMove()所做的UP、DOWN、LEFT或RIGHT值，以便它不会撤消该移动。对于对attemptMove()的初始调用，solve()函数传递 Python 的None或 JavaScript 的null值作为此参数，因为没有先前的移动存在。

attemptMove()代码的开始检查两个基本情况，如果movesRemaining变得小于0，则返回False，如果board处于解决状态，则返回True。SOLVED_BOARD常量包含一个处于解决状态的板，我们可以将其与board中的数据结构进行比较。

attemptMove()的下一部分执行它在这个板上可以做的每个有效移动。Python 代码如下：

Python

 # RECURSIVE CASE - Attempt each of the valid moves:
    for move in getValidMoves(board, prevMove):
        # Make the move:
        makeMove(board, move)
        movesMade.append(move)

        if attemptMove(board, movesMade, movesRemaining - 1, move):
            # If the puzzle is solved, return True:
            undoMove(board, move) # Reset to the original puzzle.
            return True

JavaScript 代码如下：

JavaScript

 // RECURSIVE CASE - Attempt each of the valid moves:
    for (let move of getValidMoves(board, prevMove)) {
        // Make the move:
        makeMove(board, move);
        movesMade.push(move);

        if (attemptMove(board, movesMade, movesRemaining - 1, move)) {
            // If the puzzle is solved, return True:
            undoMove(board, move); // Reset to the original puzzle.
            return true;
        }

for循环将移动变量设置为getValidMoves()返回的每个方向。对于每次移动，我们调用makeMove()来修改板数据结构并将移动添加到movesMade中的列表或数组中。

接下来，代码递归调用attemptMove()来探索由movesRemaining设置的深度内所有可能的未来移动范围。将板和movesMade变量转发到这个递归调用。代码将递归调用的movesRemaining参数设置为movesRemaining - 1，使其减少一个。它还将prevMode参数设置为move，以便它不会立即撤消刚刚做出的移动。

如果递归调用返回True，则存在解决方案，并记录在movesMade列表或数组中。我们调用undoMove()函数，以便在执行返回到solve()后，board将包含原始拼图，然后返回True以指示已找到解决方案。

Python 代码attemptMove()的继续如下：

Python

 # Undo the move to set up for the next move:
        undoMove(board, move)
        movesMade.pop() # Remove the last move since it was undone.
    return False # BASE CASE - Unable to find a solution.

JavaScript 代码如下：

JavaScript

 // Undo the move to set up for the next move:
        undoMove(board, move);
        movesMade.pop(); // Remove the last move since it was undone.
    }
    return false; // BASE CASE - Unable to find a solution.
}

如果attemptMove()返回False，则找不到解决方案。在这种情况下，我们调用undoMove()并从movesMade列表或数组中删除最新的移动。

所有这些都是针对每个有效方向完成的。如果对这些方向的attemptMove()调用在达到最大移动次数之前找到解决方案，则attemptMove()函数返回False。

开始解算器

solve()函数对于启动对attemptMove()的初始调用很有用，但程序仍然需要进行一些设置。此 Python 代码如下：

Python

# Start the program:
SOLVED_BOARD = getNewBoard()
puzzleBoard = getNewPuzzle()
displayBoard(puzzleBoard)
startTime = time.time()

此设置的 JavaScript 代码如下：

JavaScript

// Start the program:
const SOLVED_BOARD = JSON.stringify(getNewBoard());
let puzzleBoard = getNewPuzzle();
displayBoard(puzzleBoard);
let startTime = Date.now();

首先，SOLVED_BOARD常量设置为由getNewBoard()返回的有序的解决板。这个常量不是在源代码的顶部设置的，因为需要在调用它之前定义getNewBoard()函数。

接下来，从getNewPuzzle()返回一个随机拼图并存储在puzzleBoard变量中。这个变量包含将要解决的拼图板数据结构。如果您想解决特定的 15 拼图而不是随机的拼图，您可以用包含您想要解决的拼图的列表或数组替换对getNewPuzzle()的调用。

puzzleBoard中的板被显示给用户，并且当前时间存储在startTime中，以便程序可以计算算法的运行时间。Python 代码继续如下：

Python

maxMoves = 10
while True:
    if solve(puzzleBoard, maxMoves):
        break # Break out of the loop when a solution is found.
    maxMoves += 1
print('Run in', round(time.time() - startTime, 3), 'seconds.')

JavaScript 代码如下：

let maxMoves = 10;
while (true) {
    if (solve(puzzleBoard, maxMoves)) {
        break; // Break out of the loop when a solution is found.
    }
    maxMoves += 1;
}
document.write("Run in " + Math.round((Date.now() - startTime) / 100) / 10 + " seconds.
");
</script>

程序开始尝试在最多 10 步内解决puzzleBoard中的拼图。无限的while循环调用solve()。如果找到解决方案，solve()会在屏幕上打印解决方案并返回True。在这种情况下，这里的代码可以跳出无限的while循环并打印算法的总运行时间。

否则，如果solve()返回False，则maxMoves增加1，循环再次调用solve()。这使程序尝试逐渐更长的移动组合来解决拼图。这种模式一直持续到solve()最终返回True。

总结

15 拼图是将递归原则应用于现实问题的一个很好的例子。递归可以对 15 拼图产生的状态树图执行深度优先搜索，以找到通往解决方案状态的路径。然而，一个纯粹的递归算法是行不通的，这就是为什么我们不得不进行一些调整。

问题在于 15 拼图有大量可能的状态，并且不形成 DAG。图中的边是无向的，并且图中包含循环。我们的解决算法需要确保它不会进行立即撤销上一步移动的移动，以便以一个方向遍历图。它还需要有算法愿意进行的最大移动次数，然后才开始回溯；否则，循环保证算法最终会递归太多并导致堆栈溢出。

递归并不一定是解决滑块拼图的最佳方法。除了最简单的拼图之外，通常的笔记本电脑根本无法在合理的时间内解决太多的组合。然而，我喜欢 15 拼图作为递归练习，因为它将 DAGs 和 DFS 的理论思想与现实问题联系起来。虽然 15 拼图是一个多世纪前发明的，但计算机的出现为探索解决这些有趣玩具的技术提供了丰富的工具。

进一步阅读

15-puzzles 的维基百科条目en.wikipedia.org/wiki/15_puzzle详细介绍了它们的历史和数学背景。

您可以在我的书《The Big Book of Small Python Projects》（No Starch Press，2021）中找到可玩的滑块拼图游戏的 Python 源代码，并在线查看inventwithpython.com/bigbookpython/project68.html。

十三、分形艺术生成器

原文：Chapter 13 - Fractal Art Maker

译者：飞龙

协议：CC BY-NC-SA 4.0

第九章向您介绍了使用turtle Python 模块绘制许多著名分形的程序，但您也可以使用本章中的项目制作自己的分形艺术。分形艺术生成器程序使用 Python 的turtle模块将简单的形状转化为复杂的设计，只需很少的额外代码。

本章的项目带有九个示例分形，尽管您也可以编写新的函数来创建您自己设计的分形。修改示例分形以产生完全不同的艺术品，或者从头开始编写代码来实现您自己的创意愿景。

内置分形

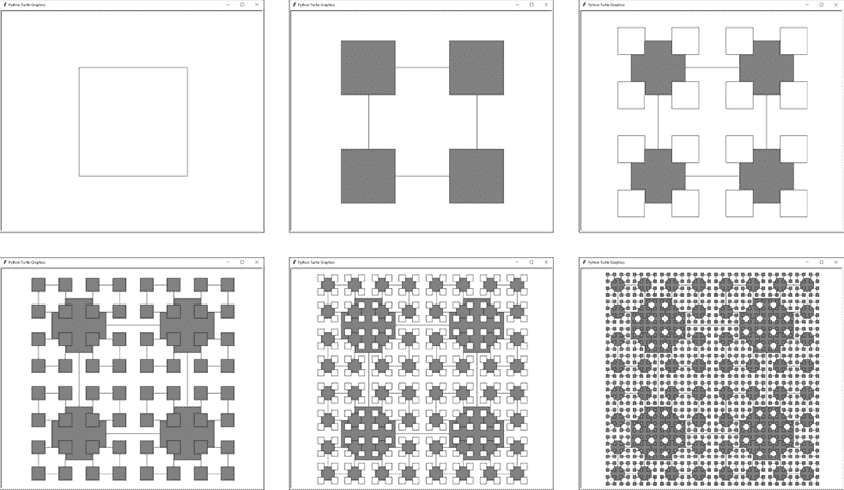
您可以指示计算机创建无限数量的分形。图 13-1 显示了本章中将使用的分形艺术生成器程序中附带的九个分形。这些是通过绘制简单的正方形或等边三角形作为基本形状，然后在它们的递归配置中引入轻微差异来产生完全不同的图像。

图 13-1：分形艺术生成器程序附带的九个示例分形

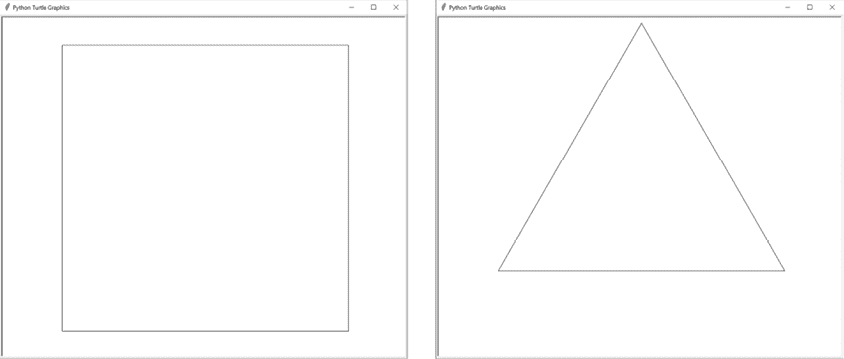
您可以通过将程序顶部的DRAW_FRACTAL常量设置为从1到9的整数，然后运行分形艺术生成器程序来生成所有这些分形。您还可以将DRAW_FRACTAL设置为10或11，以分别绘制组成这些分形的基本正方形和三角形形状，如图 13-2 所示。

图 13-2：调用drawFilledSquare()（左）和drawTriangleOutline()（右）的结果

这些形状相当简单：一个填充有白色或灰色的正方形，以及一个简单的三角形轮廓。drawFractal()函数使用这些基本形状来创建令人惊叹的分形。

分形艺术生成器算法

分形艺术生成器的算法有两个主要组成部分：一个形状绘制函数和递归的drawFractal()函数。

形状绘制函数绘制基本形状。分形艺术生成器程序配备了先前在图 13-2 中显示的两个形状绘制函数，drawFilledSquare()和drawTriangleOutline()，但您也可以创建自己的形状绘制函数。我们将一个形状绘制函数作为参数传递给drawFractal()函数，就像我们在第十章中将匹配函数传递给文件查找器的walk()函数一样。

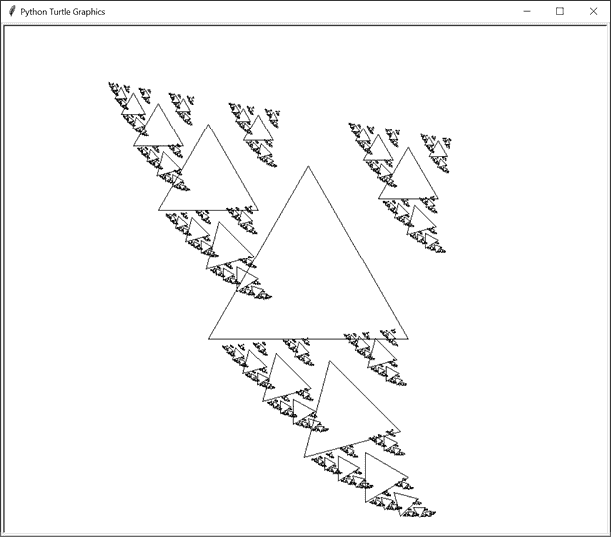
drawFractal()函数还具有一个参数，指示在对drawFractal()进行递归调用之间对形状的大小、位置和角度进行更改。我们将在本章后面介绍这些具体细节，但让我们看一个例子：分形 7，它绘制了一个波浪状的图像。

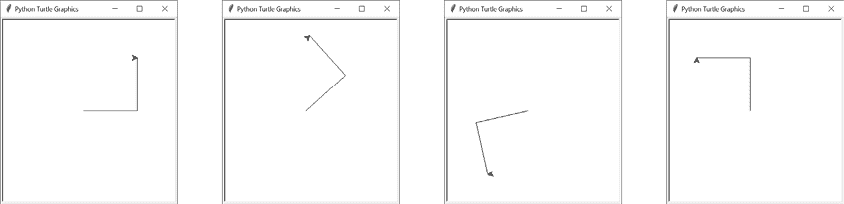
该程序通过调用drawTriangleOutline()形状绘制函数来生成波形分形，该函数创建一个单独的三角形。对drawFractal()的额外参数告诉它进行三次递归调用drawFractal()。图 13-3 显示了原始调用drawFractal()产生的三角形以及三次递归调用产生的三角形。

图 13-3：第一次调用drawFractal()产生的三角形（左）和第一组三次递归调用（右）

第一个递归调用告诉drawFractal()调用drawTriangleOutline()，但三角形的大小是上一个三角形的一半，并且位于其上一个三角形的左上方。第二个递归调用产生了一个三角形，位于其上一个三角形的右上方，大小为其 30％。第三个递归调用产生了一个三角形，位于其上一个三角形的下方，大小为其一半，并且相对于其旋转了 15 度。

这三个对drawFractal()的递归调用中的每一个都会再次对drawFractal()进行三次递归调用，从而产生九个新的三角形。新的三角形与其上一个三角形相比，其大小、位置和角度都发生了相同的变化。左上角的三角形始终是上一个三角形的一半大小，而底部三角形始终旋转 15 度。图 13-4 显示了递归的第一级和第二级产生的三角形。

图 13-4：对drawFractal()的递归调用的第一级（左）和第二级递归调用的九个新三角形（右）

对drawFractal()的这九个调用分别产生了九个新的三角形，每个调用再次对drawFractal()进行三次递归调用，从而在下一级递归中产生 27 个新的三角形。随着递归模式的继续，最终三角形变得如此小，以至于drawFractal()停止进行新的递归调用。这是递归drawFractal()函数的一个基本情况。另一个情况是当递归深度达到指定级别时。无论哪种情况，这些递归调用都会产生图 13-5 中的最终 Wave 分形。

图 13-5：每个三角形递归生成三个新三角形后的最终 Wave 分形

图 13-1 中的九个示例分形是使用两个形状绘制函数和对drawFractal()参数的一些更改制作的。让我们看看分形艺术生成器的代码，以了解它是如何实现的。

完整的分形艺术制作程序

将以下代码输入到一个新文件中，并将其保存为fractalArtMaker.py。此程序依赖于 Python 内置的turtle模块，因此本章的项目不使用 JavaScript 代码：

Python

import turtle, math

DRAW_FRACTAL = 1 # Set to 1 through 11 and run the program.

turtle.tracer(5000, 0) # Increase the first argument to speed up the drawing.
turtle.hideturtle()

def drawFilledSquare(size, depth):
    size = int(size)

    # Move to the top-right corner before drawing:
    turtle.penup()
    turtle.forward(size // 2)
    turtle.left(90)
    turtle.forward(size // 2)
    turtle.left(180)
    turtle.pendown()

    # Alternate between white and gray (with black border):
    if depth % 2 == 0:
        turtle.pencolor('black')
        turtle.fillcolor('white')
    else:
        turtle.pencolor('black')
        turtle.fillcolor('gray')

    # Draw a square:
    turtle.begin_fill()
    for i in range(4): # Draw four lines.
        turtle.forward(size)
        turtle.right(90)
    turtle.end_fill()

def drawTriangleOutline(size, depth):
    size = int(size)

    # Move the turtle to the top of the equilateral triangle:
    height = size * math.sqrt(3) / 2
    turtle.penup()
    turtle.left(90) # Turn to face upward.
    turtle.forward(height * (2/3)) # Move to the top corner.
    turtle.right(150) # Turn to face the bottom-right corner.
    turtle.pendown()

    # Draw the three sides of the triangle:
    for i in range(3):
        turtle.forward(size)
        turtle.right(120)

def drawFractal(shapeDrawFunction, size, specs, maxDepth=8, depth=0):
    if depth > maxDepth or size < 1:
        return # BASE CASE

    # Save the position and heading at the start of this function call:
    initialX = turtle.xcor()
    initialY = turtle.ycor()
    initialHeading = turtle.heading()

 # Call the draw function to draw the shape:
    turtle.pendown()
    shapeDrawFunction(size, depth)
    turtle.penup()

    # RECURSIVE CASE
    for spec in specs:
        # Each dictionary in specs has keys 'sizeChange', 'xChange',
        # 'yChange', and 'angleChange'. The size, x, and y changes
        # are multiplied by the size parameter. The x change and y
        # change are added to the turtle's current position. The angle
        # change is added to the turtle's current heading.
        sizeCh = spec.get('sizeChange', 1.0)
        xCh = spec.get('xChange', 0.0)
        yCh = spec.get('yChange', 0.0)
        angleCh = spec.get('angleChange', 0.0)

        # Reset the turtle to the shape's starting point:
        turtle.goto(initialX, initialY)
        turtle.setheading(initialHeading + angleCh)
        turtle.forward(size * xCh)
        turtle.left(90)
        turtle.forward(size * yCh)
        turtle.right(90)

        # Make the recursive call:
        drawFractal(shapeDrawFunction, size * sizeCh, specs, maxDepth, 
        depth + 1)

if DRAW_FRACTAL == 1:
    # Four Corners:
    drawFractal(drawFilledSquare, 350,
        [{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': 0.5},
         {'sizeChange': 0.5, 'xChange': 0.5, 'yChange': 0.5},
         {'sizeChange': 0.5, 'xChange': -0.5, 'yChange': -0.5},
         {'sizeChange': 0.5, 'xChange': 0.5, 'yChange': -0.5}], 5)
elif DRAW_FRACTAL == 2:
    # Spiral Squares:
    drawFractal(drawFilledSquare, 600, [{'sizeChange': 0.95,
        'angleChange': 7}], 50)
elif DRAW_FRACTAL == 3:
    # Double Spiral Squares:
    drawFractal(drawFilledSquare, 600,
        [{'sizeChange': 0.8, 'yChange': 0.1, 'angleChange': -10},
         {'sizeChange': 0.8, 'yChange': -0.1, 'angleChange': 10}])
elif DRAW_FRACTAL == 4:
    # Triangle Spiral:
    drawFractal(drawTriangleOutline, 20,
        [{'sizeChange': 1.05, 'angleChange': 7}], 80)
elif DRAW_FRACTAL == 5:
    # Conway's Game of Life Glider:
    third = 1 / 3
    drawFractal(drawFilledSquare, 600,
        [{'sizeChange': third, 'yChange': third},
 {'sizeChange': third, 'xChange': third},
         {'sizeChange': third, 'xChange': third, 'yChange': -third},
         {'sizeChange': third, 'yChange': -third},
         {'sizeChange': third, 'xChange': -third, 'yChange': -third}])
elif DRAW_FRACTAL == 6:
    # Sierpiński Triangle:
    toMid = math.sqrt(3) / 6
    drawFractal(drawTriangleOutline, 600,
        [{'sizeChange': 0.5, 'yChange': toMid, 'angleChange': 0},
         {'sizeChange': 0.5, 'yChange': toMid, 'angleChange': 120},
         {'sizeChange': 0.5, 'yChange': toMid, 'angleChange': 240}])
elif DRAW_FRACTAL == 7:
    # Wave:
    drawFractal(drawTriangleOutline, 280,
        [{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': 0.5},
         {'sizeChange': 0.3, 'xChange': 0.5, 'yChange': 0.5},
         {'sizeChange': 0.5, 'yChange': -0.7, 'angleChange': 15}])
elif DRAW_FRACTAL == 8:
    # Horn:
    drawFractal(drawFilledSquare, 100,
        [{'sizeChange': 0.96, 'yChange': 0.5, 'angleChange': 11}], 100)
elif DRAW_FRACTAL == 9:
    # Snowflake:
    drawFractal(drawFilledSquare, 200,
        [{'xChange': math.cos(0 * math.pi / 180),
          'yChange': math.sin(0 * math.pi / 180), 'sizeChange': 0.4},
         {'xChange': math.cos(72 * math.pi / 180),
          'yChange': math.sin(72 * math.pi / 180), 'sizeChange': 0.4},
         {'xChange': math.cos(144 * math.pi / 180),
          'yChange': math.sin(144 * math.pi / 180), 'sizeChange': 0.4},
         {'xChange': math.cos(216 * math.pi / 180),
          'yChange': math.sin(216 * math.pi / 180), 'sizeChange': 0.4},
         {'xChange': math.cos(288 * math.pi / 180),
          'yChange': math.sin(288 * math.pi / 180), 'sizeChange': 0.4}])
elif DRAW_FRACTAL == 10:
    # The filled square shape:
    turtle.tracer(1, 0)
    drawFilledSquare(400, 0)
elif DRAW_FRACTAL == 11:
    # The triangle outline shape:
    turtle.tracer(1, 0)
    drawTriangleOutline(400, 0)
else:
    assert False, 'Set DRAW_FRACTAL to a number from 1 to 11.'

turtle.exitonclick() # Click the window to exit.

运行此程序时，它将显示来自图 13-1 的九个分形图像中的第一个。您可以将DRAW_FRACTAL常量更改为源代码开头的任何整数，从1到9，然后再次运行程序以查看新的分形。在了解程序如何工作之后，您还可以创建自己的形状绘制函数，并调用drawFractal()来生成自己设计的分形。

设置常量和乌龟配置

程序的第一行涵盖了基于乌龟的程序的基本设置步骤：

Python

import turtle, math

DRAW_FRACTAL = 1 # Set to 1 through 11 and run the program.

turtle.tracer(5000, 0) # Increase the first argument to speed up the drawing.
turtle.hideturtle()

程序导入了用于绘图的turtle模块。它还导入了math模块，用于math.sqrt()函数，Sierpiński Triangle 分形将使用该函数，以及math.cos()和math.sin()函数，用于 Snowflake 分形。

DRAW_FRACTAL常量可以设置为从1到9的任何整数，以绘制程序生成的九个内置分形中的一个。您还可以将其设置为10或11，以分别显示正方形或三角形形状绘制函数的输出。

我们还调用一些海龟函数来准备绘制。turtle.tracer(5000, 0)调用加快了分形的绘制速度。5000参数告诉turtle模块在渲染屏幕上的绘制之前等待处理 5000 个海龟绘制指令，0参数告诉它在每个绘制指令后暂停 0 毫秒。否则，如果我们只想要最终图像，turtle模块会在每个绘制指令后渲染图像，这会显著减慢程序。

如果你想要减慢绘制速度并观察生成的线条，你可以将这个调用改为turtle.tracer(1, 10)。在制作自己的分形图案时，这可能有助于调试绘制中的任何问题。

turtle.hideturtle()调用隐藏了屏幕上代表海龟当前位置和方向的三角形形状。我们调用这个函数是为了让标记不出现在最终图像中。

使用形状绘制函数

drawFractal()函数使用传递给它的形状绘制函数来绘制分形的各个部分。这通常是一个简单的形状，比如正方形或三角形。分形的美丽复杂性是由于drawFractal()递归调用这个函数来绘制整个分形的每个组件。

Fractal Art Maker 的形状绘制函数有两个参数：size和depth。size参数是它绘制的正方形或三角形的边长。形状绘制函数应该始终使用基于size的参数来调用turtle.forward()，以便长度在每个递归级别上与size成比例。避免像turtle.forward(100)或turtle.forward(200)这样的代码；而是使用基于size参数的代码，比如turtle.forward(size)或turtle.forward(size * 2)。在 Python 的turtle模块中，turtle.forward(1)将海龟移动一个单位，这不一定等同于一个像素。

形状绘制函数的第二个参数是drawFractal()的递归深度。对drawFractal()的原始调用将depth参数设置为0。对drawFractal()的递归调用使用depth + 1作为depth参数。在 Wave 分形中，窗口中心的第一个三角形的深度参数为0。接下来创建的三个三角形的深度为1。围绕这三个三角形的九个三角形的深度为2，依此类推。

你的形状绘制函数可以忽略这个参数，但使用它可以导致基本形状的有趣变化。例如，drawFilledSquare()形状绘制函数使用depth来在绘制白色正方形和灰色正方形之间进行交替。如果你想为 Fractal Art Maker 程序创建自己的形状绘制函数，请记住它们必须接受size和depth参数。

drawFilledSquare()函数

drawFilledSquare()函数绘制了一个边长为size的填充正方形。为了给正方形上色，我们使用了turtle模块的turtle.begin_fill()和turtle.end_fill()函数，使正方形变成白色或灰色，带有黑色边框，具体取决于depth参数是偶数还是奇数。因为这些正方形是填充的，稍后绘制在它们上面的任何正方形都会覆盖它们。

就像 Fractal Art Maker 程序的所有形状绘制函数一样，drawFilledSquare()接受size和depth参数：

def drawFilledSquare(size, depth):
    size = int(size)

size参数可以是带有小数部分的浮点数，这有时会导致turtle模块绘制略微不对称和不均匀的图案。为了防止这种情况，函数的第一行将size四舍五入为整数。

当函数绘制正方形时，它假设海龟位于正方形的中心。因此，海龟必须首先移动到正方形的右上角，相对于它的初始方向：

Python

 # Move to the top-right corner before drawing:
    turtle.penup()
    turtle.forward(size // 2)
    turtle.left(90)
    turtle.forward(size // 2)
    turtle.left(180)
    turtle.pendown()

drawFractal()函数在调用形状绘制函数时总是将笔放下并准备绘制，因此drawFilledSquare()必须调用turtle.penup()以避免在移动到起始位置时绘制一条线。为了找到相对于正方形中心的起始位置，海龟必须先向前移动正方形长度的一半（即size // 2），到达正方形的未来右边缘。接下来，海龟向上转 90 度，然后向前移动size // 2个单位到达右上角。现在海龟面朝错误的方向，所以它向后转了 180 度，并放下笔，这样就可以开始绘制了。

请注意，*top-right*和*up*是相对于海龟最初面对的方向。如果海龟开始面对 0 度向右，或者其朝向为 90、42 或任何其他角度，此代码同样有效。当您创建自己的形状绘制函数时，坚持使用相对海龟移动函数，如turtle.forward()、turtle.left()和turtle.right()，而不是绝对海龟移动函数，如turtle.goto()`。

接下来，depth参数告诉函数它应该绘制白色正方形还是灰色正方形：

Python

 # Alternate between white and gray (with black border):
    if depth % 2 == 0:
        turtle.pencolor('black')
        turtle.fillcolor('white')
    else:
        turtle.pencolor('black')
        turtle.fillcolor('gray')

如果depth是偶数，则depth % 2 == 0条件为True，正方形的填充颜色为白色。否则，代码将填充颜色设置为灰色。无论哪种情况，由笔颜色确定的正方形边框都设置为黑色。要更改这两种颜色中的任何一种，请使用常见颜色名称的字符串，如red或yellow，或包含一个井号和六个十六进制数字的 HTML 颜色代码，如#24FF24表示酸橙绿，#AD7100表示棕色。

网站html-color.codes有许多 HTML 颜色代码的图表。这本黑白书中的分形缺乏颜色，但您的计算机可以以丰富的颜色范围呈现自己的分形！

颜色设置好后，我们最终可以绘制实际正方形的四条线：

Python

 # Draw a square:
    turtle.begin_fill()
    for i in range(4): # Draw four lines.
        turtle.forward(size)
        turtle.right(90)
    turtle.end_fill()

为了告诉turtle模块我们打算绘制填充形状而不仅仅是轮廓，我们调用了turtle.begin_fill()函数。接下来是一个for循环，绘制长度为size的线并将海龟向右转 90 度。for循环重复四次，以创建正方形。当函数最终调用turtle.end_fill()时，填充的正方形出现在屏幕上。

drawTriangleOutline()函数

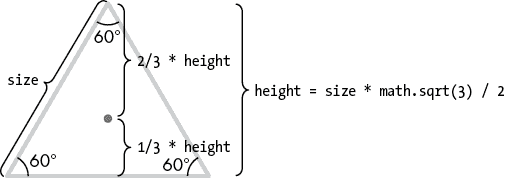
第二个形状绘制函数绘制了边长为size的等边三角形的轮廓。该函数绘制的三角形是以一个顶点在顶部，两个顶点在底部的方向。图 13-6 说明了等边三角形的各种尺寸。

图 13-6：边长为size的等边三角形的测量

在我们开始绘制之前，我们必须根据其边长确定三角形的高度。几何学告诉我们，对于边长为L的等边三角形，三角形的高度h为L乘以根号 3 除以 2。在我们的函数中，L对应于size参数，因此我们的代码设置高度变量如下：

`height = size * math.sqrt(3) / 2`

几何学还告诉我们，三角形的中心距离底边的高度为高度的三分之一，距离顶点的高度为高度的三分之二。这为我们提供了将海龟移动到起始位置所需的信息：

Python

def drawTriangleOutline(size, depth):
    size = int(size)

    # Move the turtle to the top of the equilateral triangle:
    height = size * math.sqrt(3) / 2
    turtle.penup()
    turtle.left(90) # Turn to face upward.
    turtle.forward(height * (2/3)) # Move to the top corner.
    turtle.right(150) # Turn to face the bottom-right corner.
    turtle.pendown()

为了到达顶角，我们将乌龟左转 90 度面朝上（相对于乌龟原始朝向右转 0 度），然后向前移动height * (2/3)个单位。乌龟仍然面朝上，所以要开始在右侧绘制线条，乌龟必须右转 90 度面向右侧，然后再转 60 度面向三角形的右下角。这就是为什么我们调用turtle.right(150)。

此时，乌龟已准备好开始绘制三角形，因此我们通过调用turtle.pendown()来放下画笔。for循环将处理绘制三条边：

Python

 # Draw the three sides of the triangle:
    for i in range(3):
        turtle.forward(size)
        turtle.right(120)

绘制实际三角形是向前移动size单位，然后向右转 120 度，分别进行三次。第三次和最后一次 120 度转向使乌龟面对其原始方向。您可以在图 13-7 中看到这些移动和转向。

图 13-7：绘制等边三角形涉及三次向前移动和三次 120 度转向。

drawTriangleOutline()函数只绘制轮廓而不是填充形状，因此不像drawFilledSquare()那样调用turtle.begin_fill()和turtle.end_fill()。

使用分形绘图函数

现在我们有两个样本绘图函数可以使用，让我们来看一下分形艺术制作项目中的主要函数drawFractal()。这个函数有三个必需参数和一个可选参数：shapeDrawFunction，size，specs和maxDepth。

shapeDrawFunction参数期望一个函数，比如drawFilledSquare()或drawTriangleOutline()。size参数期望传递给绘图函数的起始大小。通常，值在100到500之间是一个不错的起始大小，尽管这取决于您的形状绘制函数中的代码，并且找到合适的值可能需要进行实验。

specs参数期望一个字典列表，指定递归调用drawFractal()时递归形状应该如何改变大小、位置和角度。这些规格稍后在本节中描述。

为了防止drawFractal()递归调用导致堆栈溢出，maxDepth参数保存了drawFractal()应该递归调用自身的次数。默认情况下，maxDepth的值为8，但如果需要更多或更少的递归形状，可以提供不同的值。

第五个参数depth由drawFractal()的递归调用处理，并默认为0。调用drawFractal()时不需要指定它。

设置函数

drawFractal()函数的第一件事是检查其两个基本情况：

Python

def drawFractal(shapeDrawFunction, size, specs, maxDepth=8, depth=0):
    if depth > maxDepth or size < 1:
        return # BASE CASE

如果depth大于maxDepth，函数将停止递归并返回。另一个基本情况是如果size小于1，此时绘制的形状将太小而无法在屏幕上看到，因此函数应该简单地返回。

我们用三个变量initialX，initialY和initialHeading来跟踪乌龟的原始位置和朝向。这样，无论形状绘制函数将乌龟定位在何处或者朝向何方，drawFractal()都可以将乌龟恢复到原始位置和朝向，以便进行下一次递归调用：

Python

 # Save the position and heading at the start of this function call:
    initialX = turtle.xcor()
    initialY = turtle.ycor()
    initialHeading = turtle.heading()

turtle.xcor()和turtle.ycor()函数返回乌龟在屏幕上的绝对 x 和 y 坐标。turtle.heading()函数返回乌龟指向的方向，单位为度。

接下来的几行调用传递给shapeDrawFunction参数的形状绘制函数：

Python

 # Call the draw function to draw the shape:
    turtle.pendown()
    shapeDrawFunction(size, depth)
    turtle.penup()

由于作为shapeDrawFunction参数的值是一个函数，代码shapeDrawFunction(size, depth)调用此函数，并使用size和depth中的值。在shapeDrawFunction()调用之前和之后分别将笔降下和抬起，以确保形状绘制函数始终可以期望在绘制开始时笔是放下的。

使用规范字典

在调用shapeDrawFunction()之后，drawFractal()的其余代码致力于根据specs列表中的规范进行递归调用drawFractal()。对于每个字典，drawFractal()都会对drawFractal()进行一次递归调用。如果specs是一个具有一个字典的列表，则每次调用drawFractal()都会导致对drawFractal()的一次递归调用。如果specs是一个具有三个字典的列表，则每次调用drawFractal()都会导致对drawFractal()的三次递归调用。

specs参数中的字典为每个递归调用提供了规范。这些字典中的每一个都具有sizeChange、xChange、yChange和angleChange键。这些键规定了分形的大小、海龟的位置以及海龟的航向如何在递归的drawFractal()调用中改变。表 13-1 描述了规范中的四个键。

表 13-1：规范字典中的键

键	默认值	描述
sizeChange	1.0	下一个递归形状的大小值是当前大小乘以这个值。
xChange	0.0	下一个递归形状的 x 坐标是当前 x 坐标加上当前大小乘以这个值。
yChange	0.0	下一个递归形状的 y 坐标是当前 y 坐标加上当前大小乘以这个值。
angleChange	0.0	下一个递归形状的起始角度是当前起始角度加上这个值。

让我们来看一下四角分形的规范字典，它产生了之前在图 13-1 中显示的左上角图像。对于四角分形的drawFractal()调用，传递了以下字典列表作为specs参数：

Python

[{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': 0.5},
 {'sizeChange': 0.5, 'xChange': 0.5, 'yChange': 0.5},
 {'sizeChange': 0.5, 'xChange': -0.5, 'yChange': -0.5},
 {'sizeChange': 0.5, 'xChange': 0.5, 'yChange': -0.5}]

specs列表有四个字典，因此每次调用drawFractal()绘制一个正方形，都会递归调用drawFractal()四次，以绘制另外四个正方形。图 13-8 显示了这些正方形的进展（在白色和灰色之间交替）。

为了确定下一个要绘制的正方形的大小，sizeChange键的值乘以当前的size参数。specs列表中的第一个字典具有sizeChange值为0.5，这使得下一个递归调用具有大小参数为350 * 0.5，即175个单位。这使得下一个正方形的大小是前一个正方形的一半。例如，sizeChange值为2.0会使下一个正方形的大小加倍。如果字典没有sizeChange键，则该值默认为1.0，表示大小不变。

图 13-8：四角示例的每一步从左到右，从上到下。每个正方形在其角落递归产生四个更小的正方形，颜色在白色和灰色之间交替。

要确定下一个正方形的 x 坐标，首个字典的xChange值，在这种情况下是-0.5，乘以大小。当size为350时，这意味着下一个正方形相对于海龟当前位置有一个 x 坐标为-175单位。这个xChange值和yChange键的值为0.5，将下一个正方形的位置放置在当前正方形位置的左侧和上方 50%的距离。这恰好将其居中在当前正方形的左上角。

如果你看一下specs列表中的其他三个字典，你会注意到它们的sizeChange值都是0.5。它们之间的区别在于它们的xChange和yChange值将它们放置在当前正方形的其他三个角落。因此，下一个四个正方形是在当前正方形的四个角上居中绘制的。

这个例子中specs列表中的字典没有angleChange值，因此这个值默认为0.0度。正的angleChange值表示逆时针旋转，而负值表示顺时针旋转。

每个字典代表每次递归函数调用时要绘制的一个单独的正方形。如果我们从specs列表中删除第一个字典，每个drawFractal()调用将只产生三个正方形，就像图 13-9 中一样。

图 13-9：从specs列表中删除第一个字典的四个角分形

应用规范

让我们看看drawFractal()中的代码实际上是如何做我们描述的一切的：

Python

 # RECURSIVE CASE
    for spec in specs:
        # Each dictionary in specs has keys 'sizeChange', 'xChange',
        # 'yChange', and 'angleChange'. The size, x, and y changes
        # are multiplied by the size parameter. The x change and y
        # change are added to the turtle's current position. The angle
        # change is added to the turtle's current heading.
        sizeCh = spec.get('sizeChange', 1.0)
        xCh = spec.get('xChange', 0.0)
        yCh = spec.get('yChange', 0.0)
        angleCh = spec.get('angleChange', 0.0)

for循环将specs列表中的单个规范字典分配给循环变量spec的每次迭代。get()字典方法调用从这个字典中提取sizeChange、xChange、yChange和angleChange键的值，并将它们分配给更短的名称sizeCh、xCh、yCh和angleCh变量。如果键在字典中不存在，get()方法会替换默认值。

接下来，海龟的位置和朝向被重置为首次调用drawFractal()时指示的值。这确保了来自先前循环迭代的递归调用不会使海龟停留在其他位置。然后根据angleCh、xCh和yCh变量改变朝向和位置：

Python

 # Reset the turtle to the shape's starting point:
        turtle.goto(initialX, initialY)
        turtle.setheading(initialHeading + angleCh)

        turtle.forward(size * xCh)
        turtle.left(90)
        turtle.forward(size * yCh)
        turtle.right(90)

x-change 和 y-change 位置是相对于海龟当前的朝向来表达的。如果海龟的朝向是0，海龟的相对 x 轴与屏幕上的实际 x 轴相同。然而，如果海龟的朝向是45，海龟的相对 x 轴就会倾斜 45 度。沿着海龟的相对 x 轴“向右”移动将以一个向上和向右的角度移动。

这就是为什么通过size * xCh向前移动会沿着其相对 x 轴移动。如果xCh为负，turtle.forward()会沿着海龟的相对 x 轴向左移动。turtle.left(90)调用将海龟指向其相对 y 轴，turtle.forward(size * yCh)将海龟移动到下一个形状的起始位置。然而，turtle.left(90)调用改变了海龟的朝向，所以调用turtle.right(90)将其重置回原始方向。

图 13-10 展示了这四行代码如何沿着海龟的相对 x 轴向右移动，沿着相对 y 轴向上移动，并且无论初始朝向如何，都将其保留在正确的朝向。

图 13-10：在这四个图像中，海龟总是沿着其初始朝向的相对 x 轴和 y 轴移动 100 个单位“向右”和“向上”。

最后，当乌龟处于正确的位置和朝向下一个形状时，我们对 drawFractal()进行递归调用：

Python

 # Make the recursive call:
        drawFractal(shapeDrawFunction, size * sizeCh, specs, maxDepth, 
        depth + 1)

shapeDrawFunction，specs 和 maxDepth 参数未经修改地传递给递归 drawFractal()调用。 但是，传递 size * sizeCh 作为下一个 size 参数以反映递归形状的 size 的变化，并且传递 depth + 1 作为 depth 参数以增加下一个形状绘制函数调用的深度。

创建示例分形

既然我们已经介绍了形状绘制函数和递归 drawFractal()函数的工作原理，让我们来看看随附 Fractal Art Maker 的九个示例分形。 您可以在图 13-1 中看到这些示例。

Four Corners

第一个分形是 Four Corners，它开始作为一个大正方形。 随着函数调用自身，分形的规格导致在正方形的四个角落绘制四个较小的正方形：

Python

if DRAW_FRACTAL == 1:
    # Four Corners:
    drawFractal(drawFilledSquare, 350,
        [{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': 0.5},
         {'sizeChange': 0.5, 'xChange': 0.5, 'yChange': 0.5},
         {'sizeChange': 0.5, 'xChange': -0.5, 'yChange': -0.5},
         {'sizeChange': 0.5, 'xChange': 0.5, 'yChange': -0.5}], 5)

这里对 drawFractal()的调用将最大深度限制为 5，因为再多会使分形变得如此密集，以至于细节变得难以看清。 这个分形出现在图 13-8 中。

螺旋正方形

Spiral Squares fractal也以一个大正方形开始，但每次递归调用时只创建一个新的正方形：

Python

elif DRAW_FRACTAL == 2:
    # Spiral Squares:
    drawFractal(drawFilledSquare, 600, [{'sizeChange': 0.95,
        'angleChange': 7}], 50)

这个正方形稍小，并旋转了 7 度。 所有正方形的中心都没有改变，所以不需要向规范中添加 xChange 和 yChange 键。 默认的最大深度为 8 太小，无法得到有趣的分形，因此我们将其增加到 50 以产生催眠螺旋图案。

双螺旋正方形

Double Spiral Squares fractal类似于 Spiral Squares，只是每个正方形创建两个较小的正方形。 这会产生有趣的扇形效果，因为第二个正方形稍后绘制，往往会覆盖先前绘制的正方形：

Python

elif DRAW_FRACTAL == 3:
    # Double Spiral Squares:
    drawFractal(drawFilledSquare, 600,
        [{'sizeChange': 0.8, 'yChange': 0.1, 'angleChange': -10},
         {'sizeChange': 0.8, 'yChange': -0.1, 'angleChange': 10}])

正方形的创建略高于或低于其上一个正方形，并且旋转了 10 度或-10 度。

Triangle Spiral

Triangle Spiral fractal，螺旋正方形的另一种变体，使用 drawTriangleOutline()形状绘制函数而不是 drawFilledSquare()：

Python

elif DRAW_FRACTAL == 4:
    # Triangle Spiral:
    drawFractal(drawTriangleOutline, 20,
        [{'sizeChange': 1.05, 'angleChange': 7}], 80)

与螺旋正方形分形不同，Triangle Spiral 分形从 20 个单位的小 size 开始，并在每个递归级别略微增加大小。 sizeChange 键大于 1.0，因此形状始终在增大。 这意味着当递归达到深度 80 时，基本情况发生，因为 size 小于 1 的基本情况永远不会发生。

康威的生命游戏 Glider

康威的生命游戏是细胞自动机的著名例子。 游戏的简单规则导致在 2D 网格上出现有趣且极其混乱的图案。 其中一种图案是由 5 个单元格组成的 3×3 空间的Glider：

Python

elif DRAW_FRACTAL == 5:
    # Conway's Game of Life Glider:
    third = 1 / 3
    drawFractal(drawFilledSquare, 600,
        [{'sizeChange': third, 'yChange': third},
         {'sizeChange': third, 'xChange': third},
         {'sizeChange': third, 'xChange': third, 'yChange': -third},
         {'sizeChange': third, 'yChange': -third},
         {'sizeChange': third, 'xChange': -third, 'yChange': -third}])

这里的 Glider 分形在其五个单元格中各有额外的 Glider 绘制。 third 变量有助于精确设置 3×3 空间中递归形状的位置。

您可以在我的书《The Big Book of Small Python Projects》（No Starch Press，2021）中找到康威的生命游戏的 Python 实现，并在inventwithpython.com/bigbookpython/project13.html上找到在线版本。 不幸的是，数学家和教授约翰·康威于 2020 年 4 月因 COVID-19 并发症去世。

谢尔宾斯基三角形

我们在第九章创建了 Sierpiński Triangle 分形，但是我们的 Fractal Art Maker 也可以使用 drawTriangleOutline()形状函数重新创建它。 毕竟，谢尔宾斯基三角形是一个内部绘制了三个较小的等边三角形的等边三角形：

Python

elif DRAW_FRACTAL == 6:
    # Sierpiński Triangle:
    toMid = math.sqrt(3) / 6
    drawFractal(drawTriangleOutline, 600,
        [{'sizeChange': 0.5, 'yChange': toMid, 'angleChange': 0},
         {'sizeChange': 0.5, 'yChange': toMid, 'angleChange': 120},
         {'sizeChange': 0.5, 'yChange': toMid, 'angleChange': 240}])

这些较小三角形的中心距离上一个三角形的中心是size * math.sqrt(3) / 6单位。这三次调用将乌龟的方向调整为0、120和240度，然后在乌龟的相对 y 轴上移动。

波形

我们在本章的开头讨论了波形分形，你可以在图 13-5 中看到它。这个相对简单的分形创建了三个较小且不同的递归三角形：

Python

elif DRAW_FRACTAL == 7:
    # Wave:
    drawFractal(drawTriangleOutline, 280,
        [{'sizeChange': 0.5, 'xChange': -0.5, 'yChange': 0.5},
         {'sizeChange': 0.3, 'xChange': 0.5, 'yChange': 0.5},
         {'sizeChange': 0.5, 'yChange': -0.7, 'angleChange': 15}])

角

角分形类似于公羊的角：

Python

elif DRAW_FRACTAL == 8:
    # Horn:
    drawFractal(drawFilledSquare, 100,
        [{'sizeChange': 0.96, 'yChange': 0.5, 'angleChange': 11}], 100)

这个简单的分形由一系列正方形组成，每个正方形都比前一个正方形稍微小一些，向上移动，并旋转11度。我们将最大递归深度增加到100，以将角延伸成紧密的螺旋。

雪花

最终的分形雪花由以五边形图案布置的正方形组成。这类似于四角分形，但它使用了五个均匀间隔的递归正方形，而不是四个：

Python

elif DRAW_FRACTAL == 9:
    # Snowflake:
    drawFractal(drawFilledSquare, 200,
        [{'xChange': math.cos(0 * math.pi / 180),
          'yChange': math.sin(0 * math.pi / 180), 'sizeChange': 0.4},
         {'xChange': math.cos(72 * math.pi / 180),
          'yChange': math.sin(72 * math.pi / 180), 'sizeChange': 0.4},
         {'xChange': math.cos(144 * math.pi / 180),
          'yChange': math.sin(144 * math.pi / 180), 'sizeChange': 0.4},
         {'xChange': math.cos(216 * math.pi / 180),
          'yChange': math.sin(216 * math.pi / 180), 'sizeChange': 0.4},
         {'xChange': math.cos(288 * math.pi / 180),
          'yChange': math.sin(288 * math.pi / 180), 'sizeChange': 0.4}])

这个分形使用三角函数中的余弦和正弦函数，在 Python 的math.cos()和math.sin()函数中实现，来确定如何沿着 x 轴和 y 轴移动正方形。一个完整的圆有 360 度，所以为了均匀地在这个圆中间放置五个递归正方形，我们将它们放置在 0、72、144、216 和 288 度的间隔处。math.cos()和math.sin()函数希望角度参数是弧度而不是度数，所以我们必须将这些数字乘以math.pi / 180。

最终的结果是，每个正方形都被另外五个正方形所包围，这些正方形又被另外五个正方形所包围，依此类推，形成了一个类似雪花的晶体状分形。

生成单个正方形或三角形

为了完整起见，你还可以将DRAW_FRACTAL设置为10或11，以查看单次调用drawFilledSquare()和drawTriangleOutline()在乌龟窗口中产生的效果。这些形状的大小为600：

Python

elif DRAW_FRACTAL == 10:
    # The filled square shape:
    turtle.tracer(1, 0)
    drawFilledSquare(400, 0)
elif DRAW_FRACTAL == 11:
    # The triangle outline shape:
    turtle.tracer(1, 0)
    drawTriangleOutline(400, 0)
turtle.exitonclick() # Click the window to exit.

在根据DRAW_FRACTAL中的值绘制分形或形状之后，程序调用turtle.exitonclick()，这样乌龟窗口会一直保持打开，直到用户点击它。然后程序终止。

创建你自己的分形

你可以通过改变传递给drawFractal()函数的规范来创建自己的分形。首先考虑每次调用drawFractal()生成多少个递归调用，以及形状的大小、位置和方向应该如何改变。你可以使用现有的形状绘制函数，也可以创建自己的函数。

例如，图 13-11 展示了九个内置的分形，除了正方形和三角形函数已经交换。其中一些产生了平淡的形状，但其他一些可能会产生意想不到的美丽。

图 13-11：分形艺术制作器附带的九个分形，形状绘制函数已经交换

总结

分形艺术制作器项目展示了递归的无限可能性。一个简单的递归drawFractal()函数，配合一个绘制形状的函数，可以创造出各种各样的详细几何艺术。

在分形艺术制作器的核心是递归的drawFractal()函数，它接受另一个函数作为参数。这个第二个函数通过使用规范字典列表中给定的大小、位置和方向，重复绘制一个基本形状。

你可以测试无限数量的形状绘制函数和规范设置。让你的创造力驱动你的分形项目，当你在这个程序中进行实验时。

进一步阅读

有一些网站可以让您创建分形。交互式分形树在www.visnos.com/demos/fractal上有滑块可以改变二叉树分形的角度和大小参数。procedural-snowflake.glitch.me上的程序性雪花可以在您的浏览器中生成新的雪花。Nico 的分形机在sciencevsmagic.net/fractal上创建分形的动画图。您可以通过在网络上搜索分形生成器或在线分形生成器来找到其他网站。

十四、Droste 生成器

原文：Chapter 14 - Droste Maker

译者：飞龙

协议：CC BY-NC-SA 4.0

Droste 效应是一种递归艺术技术，以荷兰品牌 Droste 可可的 1904 年插图命名。在图 14-1 中，这个罐子上有一个护士拿着一个托盘，托盘上有一个 Droste 可可的罐子，罐子上有这个插图。

在本章中，我们将创建一个 Droste 生成器程序，可以从您拥有的任何照片或图纸生成类似的递归图像，无论是一个在博物馆观看自己展品的参观者，一只猫在另一只猫前面的计算机显示器，还是其他任何东西。

图 14-1: Droste 可可罐上的递归插图

使用诸如 Microsoft Paint 或 Adobe Photoshop 之类的图形程序，您将通过用纯品红色覆盖图像的一部分来准备图像，指示递归图像的放置位置。Python 程序使用 Pillow 图像库读取这些图像数据并生成递归图像。

首先，我们将介绍如何安装 Pillow 库以及 Droste 生成器算法的工作原理。接下来，我们将提供程序的 Python 源代码，并解释代码。

安装 Pillow Python 库

本章的项目需要 Pillow 图像库。这个库允许您的 Python 程序创建和修改图像文件，包括 PNG、JPEG 和 GIF。它有几个函数可以执行调整大小、复制、裁剪和其他常见的图像操作。

要在 Windows 上安装此库，请打开命令提示窗口并运行py -m pip install --user pillow。要在 macOS 或 Linux 上安装此库，请打开终端窗口并运行 python3 -m pip install --user pillow。此命令使 Python 使用 pip 安装程序从pypi.org官方 Python 软件包索引下载模块。

要验证安装是否成功，请打开 Python 终端并运行from PIL import Image。（虽然库的名称是 Pillow，但安装的 Python 模块名为PIL，大写字母。）如果没有出现错误，则库已正确安装。

Pillow 的官方文档可以在pillow.readthedocs.io找到。

绘制您的图像

下一步是通过将图像的一部分设置为 RGB（红色、绿色、蓝色）颜色值（255, 0, 255）来准备图像。计算机图形通常使用品红色来标记图像的哪些像素应该被渲染为透明。我们的程序将把这些品红色像素视为视频制作中的绿屏，用初始图像的调整版本替换它们。当然，这个调整后的图像将有自己更小的品红区域，程序将用另一个调整后的图像替换它。当最终图像没有更多品红像素时，基本情况发生，此时算法完成。

图 14-2 显示了随着调整大小的图像递归应用到品红色像素而创建的图像的进展。在这个例子中，一个模特站在一个被品红色像素替换的艺术博物馆展品前，将照片本身变成了展品。你可以从inventwithpython.com/museum.png下载这个基础图像。

确保在你的图像中只使用纯(255, 0, 255)品红色来绘制品红色区域。一些工具可能会产生淡化效果，产生更自然的外观。例如，Photoshop 的画笔工具会在绘制区域的轮廓上产生淡化的品红色像素，所以你需要使用铅笔工具，它只使用你选择的精确纯品红色来绘制。如果你的图形程序不允许你指定绘制的精确 RGB 颜色，你可以从inventwithpython.com/magenta.png的 PNG 图像中复制和粘贴颜色。

图像中的品红色区域可以是任意大小或形状；它不必是一个精确的、连续的矩形。你可以在图 14-2 中看到，博物馆参观者切入品红色矩形，将他们放在递归图像的前面。

如果你用 Droste Maker 制作自己的图像，你应该使用 PNG 图像文件格式而不是 JPEG。JPEG 图像使用有损压缩技术来保持文件大小小，引入了轻微的瑕疵。这些通常对人眼来说是不可察觉的，不会影响整体图像质量。然而，这种有损压缩会用稍微不同色调的品红色像素取代纯(255, 0, 255)品红色。PNG 图像的无损压缩确保这种情况不会发生。

图 14-2：图像递归应用到品红色像素。如果你在本书中查看黑白图像，品红色区域是博物馆参观者前面的矩形。

完整的 Droste Maker 程序

以下是drostemaker.py的源代码；因为这个程序依赖于仅限于 Python 的 Pillow 库，所以在本书中这个项目没有 JavaScript 的等价物：

from PIL import Image

def makeDroste(baseImage, stopAfter=10):
    # If baseImage is a string of an image filename, load that image:
    if isinstance(baseImage, str):
        baseImage = Image.open(baseImage)

    if stopAfter == 0:
        # BASE CASE
        return baseImage
    # The magenta color has max red/blue/alpha, zero green:
    if baseImage.mode == 'RGBA':
        magentaColor = (255, 0, 255, 255)
    elif baseImage.mode == 'RGB':
        magentaColor = (255, 0, 255)

    # Find the dimensions of the base image and its magenta area:
    baseImageWidth, baseImageHeight = baseImage.size
    magentaLeft = None
    magentaRight = None
    magentaTop = None
    magentaBottom = None

    for x in range(baseImageWidth):
        for y in range(baseImageHeight):
            if baseImage.getpixel((x, y)) == magentaColor:
                if magentaLeft is None or x < magentaLeft:
                    magentaLeft = x
                if magentaRight is None or x > magentaRight:
                    magentaRight = x
                if magentaTop is None or y < magentaTop:
                    magentaTop = y
                if magentaBottom is None or y > magentaBottom:
                    magentaBottom = y

    if magentaLeft is None:
        # BASE CASE - No magenta pixels are in the image.
        return baseImage

    # Get a resized version of the base image:
    magentaWidth = magentaRight - magentaLeft + 1
    magentaHeight = magentaBottom - magentaTop + 1
    baseImageAspectRatio = baseImageWidth / baseImageHeight
    magentaAspectRatio = magentaWidth / magentaHeight

    if baseImageAspectRatio < magentaAspectRatio:
        # Make the resized width match the width of the magenta area:
        widthRatio = magentaWidth / baseImageWidth
        resizedImage = baseImage.resize((magentaWidth, 
        int(baseImageHeight * widthRatio) + 1), Image.NEAREST)
    else:
        # Make the resized height match the height of the magenta area:
        heightRatio =  magentaHeight / baseImageHeight
 resizedImage = baseImage.resize((int(baseImageWidth * 
        heightRatio) + 1, magentaHeight), Image.NEAREST)

    # Replace the magenta pixels with the smaller, resized image:
    for x in range(magentaLeft, magentaRight + 1):
        for y in range(magentaTop, magentaBottom + 1):
            if baseImage.getpixel((x, y)) == magentaColor:
                pix = resizedImage.getpixel((x - magentaLeft, y - magentaTop))
                baseImage.putpixel((x, y), pix)

    # RECURSIVE CASE:
    return makeDroste(baseImage, stopAfter=stopAfter - 1)

recursiveImage = makeDroste('museum.png')
recursiveImage.save('museum-recursive.png')
recursiveImage.show()

在运行这个程序之前，将你的图像文件放在与drostemaker.py相同的文件夹中。程序将递归图像保存为museum-recursive.png，然后打开一个图像查看器来显示它。如果你想在你自己添加了品红色区域的图像上运行程序，用你的图像文件的名称替换源代码末尾的makeDroste('museum.png')，用你想要用来保存递归图像的名称替换save('museum-recursive.png')。

设置

Droste Maker 程序只有一个函数makeDroste()，它接受一个 Pillow Image对象或一个图像文件名的字符串。该函数返回一个 Pillow Image对象，其中任何品红色像素都被同一图像的版本递归地替换：

Python

from PIL import Image

def makeDroste(baseImage, stopAfter=10):
    # If baseImage is a string of an image filename, load that image:
    if isinstance(baseImage, str):
        baseImage = Image.open(baseImage)

程序开始时从 Pillow 库（作为 Python 模块命名为PIL）导入Image类。在makeDroste()函数内部，我们检查baseImage参数是否是一个字符串，如果是，我们将其替换为从相应图像文件加载的 Pillow Image对象。

接下来，我们检查stopAfter参数是否为0。如果是，我们已经达到了算法的一个基本情况，函数将返回基础图像的 Pillow Image对象：

Python

 if stopAfter == 0:
        # BASE CASE
        return baseImage

如果函数调用没有提供stopAfter，则stopAfter参数默认为10。在此函数中稍后对makeDroste()的递归调用将stopAfter - 1作为该参数的参数传递，以便它在每次递归调用时减少，并接近0的基本情况。

例如，将0传递给stopAfter会导致函数立即返回与基本图像相同的递归图像。将1传递给stopAfter会替换品红区域为递归图像一次，进行一次递归调用，达到基本情况，并立即返回。将2传递给stopAfter会导致两次递归调用，依此类推。

该参数防止函数在品红区域特别大时递归，直到导致堆栈溢出。它还允许我们传递比10更小的参数，以限制放置在基本图像中的递归图像的数量。例如，通过为stopAfter参数传递0、1、2和3，可以创建图 14-2 中的四幅图像。

接下来，我们检查基本图像的颜色模式。这可以是RGB，表示具有红绿蓝像素的图像，或者RGBA，表示具有像素 alpha 通道的图像。alpha 值表示像素的透明级别。以下是代码：

Python

 # The magenta color has max red/blue/alpha, zero green:
    if baseImage.mode == 'RGBA':
        magentaColor = (255, 0, 255, 255)
    elif baseImage.mode == 'RGB':
        magentaColor = (255, 0, 255)

Droste Maker 需要知道颜色模式，以便它可以找到品红像素。每个通道的值范围从0到255，品红像素具有最大量的红色和蓝色，但没有绿色。此外，如果存在 alpha 通道，对于完全不透明的颜色，它将设置为255，对于完全透明的颜色，它将设置为0。根据baseImage.mode中给出的图像颜色模式，magentaColor变量设置为品红像素的正确元组值。

寻找品红区域

在程序可以递归地将图像插入品红区域之前，它必须找到图像中品红区域的边界。这涉及找到图像中最左、最右、最上和最下的品红像素。

虽然品红区域本身不需要是一个完美的矩形，但程序需要知道品红的矩形边界，以便正确调整图像以进行插入。例如，图 14-3 显示了蒙娜丽莎的基本图像，其中品红区域用白色轮廓标出。品红像素被替换以生成递归图像。

图 14-3：带有白色轮廓的品红区域的基本图像（左）及其生成的递归图像（右）

为了计算调整大小和调整后图像的放置位置，程序从baseImage中 PillowImage对象的size属性中检索基本图像的宽度和高度。以下行初始化了四个变量，用于品红区域的四个边缘——magentaLeft，magentaRight，magentaTop和magentaBottom——并将其值设置为None：

Python

 # Find the dimensions of the base image and its magenta area:
    baseImageWidth, baseImageHeight = baseImage.size
    magentaLeft = None
    magentaRight = None
    magentaTop = None
    magentaBottom = None

这些边缘变量的值在接下来的代码中被整数x和y坐标替换：

Python

 for x in range(baseImageWidth):
        for y in range(baseImageHeight):
            if baseImage.getpixel((x, y)) == magentaColor:
                if magentaLeft is None or x < magentaLeft:
                    magentaLeft = x
                if magentaRight is None or x > magentaRight:
                    magentaRight = x
                if magentaTop is None or y < magentaTop:
                    magentaTop = y
                if magentaBottom is None or y > magentaBottom:
                    magentaBottom = y

这些嵌套的for循环在基本图像的每个可能的 x、y 坐标上迭代x和y变量。我们检查每个坐标处的像素是否为存储在magentaColor中的纯品红色，然后更新magentaLeft变量，如果品红像素的坐标比magentaLeft中当前记录的更靠左，则对其他三个方向也是如此。

当嵌套的for循环完成时，magentaLeft，magentaRight，magentaTop和magentaBottom将描述基本图像中品红像素的边界。如果图像没有品红像素，这些变量将保持设置为它们最初的None值：

Python

 if magentaLeft is None:
        # BASE CASE - No magenta pixels are in the image.
        return baseImage

如果嵌套的for循环完成后magentaLeft（或者实际上是这四个变量中的任何一个）仍然设置为None，则图像中没有品红像素。这是我们递归算法的基本情况，因为随着每次对makeDroste()的递归调用，品红区域会变得越来越小。此时，函数返回baseImage中的 PillowImage对象。

调整基本图像的大小

我们需要将基本图像调整大小以完全覆盖品红区域，不多不少。图 14-4 显示了完整的调整大小后的图像透明地叠加在原始基本图像上。这个调整大小后的图像被裁剪，以便只有覆盖品红像素的部分被复制到最终图像中。

图 14-4：带有显示器中品红区域的基本图像（顶部），覆盖在基本图像上的调整大小后的图像（中部），以及替换仅品红像素的最终递归图像（底部）

我们不能简单地将基本图像调整大小到品红区域的尺寸，因为两者不太可能具有相同的长宽比，即宽度除以高度的比例。这样做会导致一个看起来被拉伸或压缩的递归图像，就像图 14-5 一样。

相反，我们必须使调整大小后的图像足够大，以完全覆盖品红区域，但仍保留图像的原始长宽比。这意味着要么将调整大小后的图像的宽度设置为品红区域的宽度，使得调整大小后的图像的高度等于或大于品红区域的高度，要么将调整大小后的图像的高度设置为品红区域的高度，使得调整大小后的图像的宽度等于或大于品红区域的宽度。

图 14-5：将图像调整大小到品红区域的尺寸可能会导致不同的长宽比，使其看起来被拉伸或压缩。

为了计算正确的调整尺寸，程序需要确定基本图像和品红区域的长宽比：

Python

 # Get a resized version of the base image:
    magentaWidth = magentaRight - magentaLeft + 1
    magentaHeight = magentaBottom - magentaTop + 1
    baseImageAspectRatio = baseImageWidth / baseImageHeight
    magentaAspectRatio = magentaWidth / magentaHeight

从magentaRight和magentaLeft，我们可以计算出品红区域的宽度。+1是为了一个小的必要调整：如果品红区域的右侧 x 坐标为 11，左侧为 10，宽度将为两个像素。这是通过(magentaRight - magentaLeft + 1)正确计算的，而不是(magentaRight - magentaLeft)。

因为长宽比是宽度除以高度，具有大长宽比的图像比宽度大，具有小长宽比的图像比高度大。长宽比为 1.0 描述了一个完美的正方形。接下来的行设置了基本图像和品红区域的长宽比后调整大小图像的尺寸：

 if baseImageAspectRatio < magentaAspectRatio:
        # Make the resized width match the width of the magenta area:
        widthRatio = magentaWidth / baseImageWidth
        resizedImage = baseImage.resize((magentaWidth, 
        int(baseImageHeight * widthRatio) + 1), Image.NEAREST)
 else:
        # Make the resized height match the height of the magenta area:
        heightRatio =  magentaHeight / baseImageHeight
        resizedImage = baseImage.resize((int(baseImageWidth * 
        heightRatio) + 1, magentaHeight), Image.NEAREST)

如果基础图像的宽高比小于品红色区域的宽高比，则调整大小后的图像的宽度应与品红色区域的宽度匹配。如果基础图像的宽高比大，则调整大小后的图像的高度应与品红色区域的高度匹配。然后，我们通过将基础图像的高度乘以宽度比例或将基础图像的宽度乘以高度比例来确定另一个维度。这确保了调整大小后的图像既完全覆盖品红色区域，又保持与其原始宽高比的比例。

我们调用resize()方法一次，以生成一个新的 PillowImage对象，其大小与基础图像的宽度或高度匹配。第一个参数是一个(宽度，高度)元组，用于新图像的大小。第二个参数是 Pillow 库中的Image.NEAREST常量，告诉resize()方法在调整图像大小时使用最近邻算法。这可以防止resize()方法混合像素颜色以产生平滑的图像。

我们不希望这样，因为这可能会使调整大小后的图像中的品红色像素与相邻的非品红色像素模糊在一起。我们的makeDroste()函数依赖于检测具有精确 RGB 颜色(255, 0, 255)的品红色像素，并且会忽略这些略微偏离的品红色像素。最终结果将是品红色区域周围有一个粉红色的轮廓，这将破坏我们的图像。最近邻算法不会进行这种模糊处理，使我们的品红色像素恰好保持在(255, 0, 255)的品红色。

在图像中递归放置图像

基础图像调整大小后，我们可以将调整大小后的图像放置在基础图像上。但是，调整大小后的图像的像素应该只放置在基础图像中的品红色像素上。调整大小后的图像将被放置在这样一个位置，即调整大小后的图像的左上角位于品红色区域的左上角：

Python

 # Replace the magenta pixels with the smaller, resized image:
    for x in range(magentaLeft, magentaRight + 1):
        for y in range(magentaTop, magentaBottom + 1):
            if baseImage.getpixel((x, y)) == magentaColor:
                pix = resizedImage.getpixel((x - magentaLeft, y - magentaTop))
                baseImage.putpixel((x, y), pix)

两个嵌套的for循环遍历品红色区域中的每个像素。请记住，品红色区域不一定是一个完美的矩形，因此我们要检查当前坐标处的像素是否为品红色。如果是，我们从调整大小后的图像中获取相应坐标处的像素颜色，并将其放置在基础图像上。两个嵌套的for循环完成循环后，基础图像中的品红色像素将被调整大小后的图像中的像素替换。

然而，调整大小后的图像本身可能有品红色的像素，如果是这样，这些像素现在将成为基础图像的一部分，就像图 14-2 的右上图中一样。我们需要将修改后的基础图像传递给递归的makeDroste()调用：

Python

 # RECURSIVE CASE:
    return makeDroste(baseImage, stopAfter - 1)

这一行是我们递归算法中的递归调用，也是makeDroste()函数中的最后一行代码。这种递归处理了从调整大小后的图像复制的新品红色区域。请注意，传递给stopAfter参数的值是stopAfter - 1，确保它更接近0的基本情况。

最后，Droste Maker 程序通过将′museum.png′传递给makeDroste()来开始，以获得递归图像的 PillowImage对象。我们将其保存为一个名为museum-recursive.png的新图像文件，并在新窗口中显示递归图像供用户查看：

Python

recursiveImage = makeDroste('museum.png')
recursiveImage.save('museum-recursive.png')
recursiveImage.show()

您可以将这些文件名更改为计算机上您想要与程序一起使用的任何图像。

makeDroste()函数需要使用递归实现吗？简单地说，不需要。请注意，问题中没有涉及类似树状结构，并且算法不进行回溯，这表明递归可能是对这段代码过度设计的方法。

总结

本章的项目是一个程序，可以生成递归 Droste 效应图像，就像 Droste 的 Cacao 旧罐头上的插图一样。该程序通过使用纯品红像素（RGB 值为（255, 0, 255））来标记图像中应该被较小版本替换的部分来工作。由于这个较小的版本也将有自己较小的品红区域，替换将重复进行，直到品红区域消失以生成递归图像。

我们递归算法的基本情况是当图像中没有更多品红像素可以放置较小的递归图像，或者stopAfter计数器达到0时。否则，递归情况将图像传递给makeDroste()函数，以继续用更小的递归图像替换品红区域。

您可以修改自己的照片以添加品红像素，然后通过 Droste Maker 运行它们。在一个展览中观看自己的博物馆参观者，猫坐在猫前面的计算机显示器前，以及无面孔的《蒙娜丽莎》图像只是您可以用这个递归程序创造的超现实可能性的一些例子。

进一步阅读

维基百科关于 Droste 效应的文章en.wikipedia.org/wiki/Droste_effect中有除 Droste 的 Cacao 之外使用 Droste 效应的产品的例子。荷兰艺术家 M.C. Escher 的作品《Print Gallery》是一个著名的场景，其中也包含了自身，您可以在en.wikipedia.org/wiki/Print_Gallery_(M._C._Escher)了解更多信息。

在 Numberphile YouTube 频道上名为“The Neverending Story (and Droste Effect)”的视频中，Clifford Stoll 博士讨论了递归和 Droste 的 Cacao 盒子艺术youtu.be/EeuLDnOupCI。

我的书《Automate the Boring Stuff with Python》第二版（No Starch Press，2019）的第十九章提供了 Pillow 库的基本教程automatetheboringstuff.com/2e/chapter19。