【手搓深度学习算法】从头创建卷积神经网络
背景
深度学习神经网络中,卷积神经网络在图像处理中独放异彩,现在主流的框架中对卷积神经网络的封装已经非常完善了,但是,对初学者来说,使用这些高层的API,不利于我们深入理解卷积神经网络的原理和思想,所以,想要动手实现一个简单的卷积神经网络,通过查阅资料,参考他人的代码,总结了这篇文档。
术语解释
卷积神经网络(Convolutional Neural Network,CNN)是一种深度学习神经网络结构,主要用于图像识别、计算机视觉等领域。该结构在处理图像等高维数据时表现出色,因为它具有共享权重和局部感知的特点,一方面减少了权值的数量使得网络易于优化,另一方面降低了模型的复杂度,也就是减小了过拟合的风险。
卷积神经网络主要由卷积层、池化层、全连接层和激活函数等组成。其中,卷积层是CNN的核心部分,它通过卷积操作提取输入图像的特征,并将这些特征作为下一层的输入。池化层则用于降采样,可以减少卷积层输出的特征图的大小,从而减少网络参数和计算量。全连接层则用于将卷积层和池化层的输出连接起来,以便最终进行分类和预测。
卷积神经网络的训练主要是通过反向传播算法来更新网络中的权重,从而使得网络能够逐步学习到输入数据的特征,并在最终的分类或预测任务中得到较好的性能。
目前,卷积神经网络已经在图像分类、物体识别、人脸识别、自然语言处理等领域取得了非常出色的成果,是现代深度学习领域的重要组成部分。
为什么要使用卷积神经网络
使用卷积神经网络(CNN)的原因主要有以下几点:
局部感知: CNN能处理局部输入。这是因为在CNN中,每一个神经元只接收输入区域的小部分数据,这使得网络能够专注于局部特征,而不是全局特征。
权重共享: 在CNN中,权重是共享的。这意味着无论在图像的哪个位置,同一卷积核都会进行相同的操作。这不仅减少了模型的参数数量,还增强了模型对平移不变性的处理能力。
池化层(Pooling): 池化层用于降低数据的维度,减少计算量,同时保留重要信息。这有助于防止过拟合,提高模型的泛化能力。
多层次特征提取: CNN通过逐层卷积和池化操作,能够从底层到高层提取并逐渐抽象出图像中的特征。这使得CNN在处理图像、语音等高维数据时具有显著的优势。
强大的表达能力: 通过设计不同的卷积核,CNN能够学习并表达多种特征。此外,多层卷积能够让模型在更抽象的层次上理解输入数据。
有效利用数据: 对于具有大量标注数据的场景,CNN能够有效地利用这些数据进行训练,从而提高模型的准确率。
并行计算能力: 由于卷积操作具有局部性和权重共享的特性,CNN非常适合进行并行计算,这大大提高了模型的训练速度。
综上所述,由于以上优点,卷积神经网络在图像识别、计算机视觉、自然语言处理等领域得到了广泛应用。
任务描述
本项目旨在使用基本Python库和Numpy库,实现一个简单的卷积神经网络模型,包括一个卷积核为3 * 3 的卷积层,一个最大池化层,和一个使用softmax函数的全连接层
具体实现
定义一个卷积层
备注:我们定义的卷积层假设输入是2维的numpy数组,只存在一个卷积层且Batch为1
以下是在名为Conv3x3的类中的内容
在初始化中定义卷积核*这段代码通过传入的num_filters参数定义输出数据的维度,然后创建随机的3x3的卷积核,
使用除以9,用于初始化卷积核的权重,将其缩放到一个较小的值范围(这里是0到1/9之间)。这种初始化方法可以帮助防止在训练过程中出现梯度消失或梯度爆炸的问题。*
def __init__(self, num_filters):
self.num_filters = num_filters
self.filters = np.random.randn(num_filters, 3, 3) / 9
生成感受野的迭代器
先获取图像的宽高,然后在图像上以步长为1滑动3x3的卷积窗口,得到(感受野,x,y)的迭代器
def iterate_regions(self, image):
h, w = image.shape
for i in range(h - 2):
for j in range(w - 2):
im_region = image[i:(i + 3), j:(j + 3)]
yield im_region, i, j
定义前向传播的函数
卷积网络的前向传播过程即将卷积核和感受野进行加权求和,然后迭代每一个卷积核输出n维的特征向量
def forward(self, input):
self.last_input = input
h, w = input.shape
output = np.zeros((h - 2, w - 2, self.num_filters))
for im_region, i, j in self.iterate_regions(input):
output[i, j] = np.sum(im_region * self.filters, axis=(1, 2))
return output
定义反向传播的函数
卷积网络的反向传播可以简单的理解为,通过损失函数的梯度更新卷积层的权重,即卷积核的权重,其中损失函数的梯度可以简单理解为在损失函数中对权重和偏差求偏导数,更新权重的过程中,使用了超参数学习率,通过改变学习率的大小,可以改变模型的收敛速度和精度。
其中,每个卷积核都经历了i * j轮的迭代,通过对应感受野梯度和像素值的点积得到权重更新的梯度
注意:这里作者为了偷懒,只用了一层卷积层,而且卷积层是第一个网络层,所以卷积层的反向传播函数不需要返回梯度
def backprop(self, d_L_d_out, learn_rate):
d_L_d_filters = np.zeros(self.filters.shape)
for im_region, i, j in self.iterate_regions(self.last_input):
for f in range(self.num_filters):
d_L_d_filters[f] += d_L_d_out[i, j, f] * im_region
self.filters -= learn_rate * d_L_d_filters
return None
定义一个最大池化层
卷积神经网络(CNN)中的最大池化层主要有以下作用:
增加特征平移不变性:池化层可以提高网络对微小位移的容忍能力,增强特征的鲁棒性。
减小特征图大小:池化层对空间局部区域进行下采样,使下一层需要的参数量和计算量减少,并降低过拟合风险。
引入非线性:最大池化可以带来非线性,这是目前最大池化更常用的原因之一。
不同的区域迭代器
生成不重叠的2x2图像区域,用于池化操作。
def iterate_regions(self, image):
h, w, _ = image.shape
new_h = h // 2
new_w = w // 2
for i in range(new_h):
for j in range(new_w):
im_region = image[(i * 2):(i * 2 + 2), (j * 2):(j * 2 + 2)]
yield im_region, i, j
前向传播函数
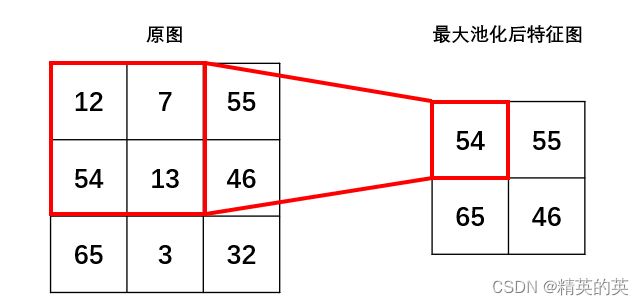
最大池化层的前向传播过程即是以指定的池化核大小作为窗口,在输入特征图上进行不重叠的滑动,每次取当前窗口内的最大值,生成新的特征图,对2*2的池化层,因为每个池化窗口内的特征数量从 2 * 2 变成 1 * 1,所以图像的尺寸将会变成输入图的一半,减少了模型的复杂程度,同时,每个池化窗口内删除了3/4的特征值,可以让特征更好的体现非线性,又因为每个池化窗口内只取最大值,可以保留输入特征图的重要特征。
def forward(self, input):
self.last_input = input
h, w, num_filters = input.shape
output = np.zeros((h // 2, w // 2, num_filters))
for im_region, i, j in self.iterate_regions(input):
output[i, j] = np.amax(im_region, axis=(0, 1))
return output
反向传播函数
最大池化层的反向传播函数可以简单理解为,通过其输出梯度更新池化之前的特征图上每个池化感受野上特征值最大的点的梯度,其他位置的梯度为0。
def backprop(self, d_L_d_out):
d_L_d_input = np.zeros(self.last_input.shape)
for im_region, i, j in self.iterate_regions(self.last_input):
h, w, f = im_region.shape
amax = np.amax(im_region, axis=(0, 1))
#计算每个区域的最大值。这将返回一个数组,其中包含每个通道的最大值。
for i2 in range(h):
for j2 in range(w):
for f2 in range(f):
# 如果当前特征点是特征值最大的点,将输出梯度矩阵中对应的梯度值复制到输入梯度矩阵中每个感受野的最大值位置
if im_region[i2, j2, f2] == amax[f2]:
d_L_d_input[i * 2 + i2, j * 2 + j2, f2] = d_L_d_out[i, j, f2]
return d_L_d_input
定义一个Softmax层
Softmax是一种激活函数,用于将指定的输入向量转化成指定种类别的输出概率
y i = exp ( a i ) ∑ j = 1 n exp ( a j ) y_i = \frac{\exp(a_i)}{\sum_{j=1}^{n} \exp(a_j)} yi=∑j=1nexp(aj)exp(ai)
初始化权重和偏差
初始化本层的权重和偏差,权重应该是 输入节点数量 x 分类数量 的矩阵,以便和前一层的输出特征矩阵做点积。
def __init__(self, input_len, nodes):
self.weights = np.random.randn(input_len, nodes) / input_len
self.biases = np.zeros(nodes)
前向传播函数
Softmax的前向传播函数的作用:
- 将数据展平,比如:输入特征是5维28*28的张量,则展平后数据变成长度为5x28x28的向量。
- 将展平后的向量与本层的权重做点积,然后加上本层的偏差向量,得到本层输出的向量。
- 将本层的输出向量做如上公式的计算,得到每个类别的概率。
def forward(self, input):
self.last_input_shape = input.shape
input = input.flatten()
self.last_input = input
input_len, nodes = self.weights.shape
totals = np.dot(input, self.weights) + self.biases
self.last_totals = totals
exp = np.exp(totals)
return exp / np.sum(exp, axis=0)
反向传播函数
Softmax的反向传播函数即是对Softmax的前向传播函数逐层计算梯度
假设Softmax层的输入为向量 z \mathbf{z} z,其第 i i i个元素为 z i z_i zi,输出为向量 a \mathbf{a} a,其第 i i i个元素为 a i a_i ai。Softmax函数定义为:
a i = e z i ∑ j = 1 n e z j a_i = \frac{e^{z_i}}{\sum_{j=1}^{n}e^{z_j}} ai=∑j=1nezjezi
其中, n n n是输入向量 z \mathbf{z} z的长度。
在反向传播过程中,我们需要计算损失函数 L L L对于输入向量 z \mathbf{z} z的梯度 ∂ L ∂ z \frac{\partial L}{\partial \mathbf{z}} ∂z∂L。根据链式法则,我们有:
∂ L ∂ z i = ∑ j = 1 n ∂ L ∂ a j ∂ a j ∂ z i \frac{\partial L}{\partial z_i} = \sum_{j=1}^{n}\frac{\partial L}{\partial a_j}\frac{\partial a_j}{\partial z_i} ∂zi∂L=∑j=1n∂aj∂L∂zi∂aj
其中, ∂ L ∂ a j \frac{\partial L}{\partial a_j} ∂aj∂L是损失函数 L L L对于输出向量 a \mathbf{a} a的梯度,它可以根据具体的损失函数计算得到。接下来,我们需要计算 ∂ a j ∂ z i \frac{\partial a_j}{\partial z_i} ∂zi∂aj。
当 i = j i=j i=j时,我们有:
∂ a i ∂ z i = e z i ∑ j = 1 n e z j − e 2 z i ( ∑ j = 1 n e z j ) 2 = a i ( 1 − a i ) \frac{\partial a_i}{\partial z_i} = \frac{e^{z_i}\sum_{j=1}^{n}e^{z_j} - e^{2z_i}}{(\sum_{j=1}^{n}e^{z_j})^2} = a_i(1-a_i) ∂zi∂ai=(∑j=1nezj)2ezi∑j=1nezj−e2zi=ai(1−ai)
当 i ≠ j i \neq j i=j时,我们有:
∂ a j ∂ z i = − e z i e z j ( ∑ k = 1 n e z k ) 2 = − a i a j \frac{\partial a_j}{\partial z_i} = \frac{-e^{z_i}e^{z_j}}{(\sum_{k=1}^{n}e^{z_k})^2} = -a_ia_j ∂zi∂aj=(∑k=1nezk)2−eziezj=−aiaj
将上述结果代入链式法则中,我们得到:
∂ L ∂ z i = ∂ L ∂ a i a i ( 1 − a i ) − ∑ j ≠ i ∂ L ∂ a j a i a j = a i ( ∂ L ∂ a i − ∑ j = 1 n ∂ L ∂ a j a j ) \frac{\partial L}{\partial z_i} = \frac{\partial L}{\partial a_i}a_i(1-a_i) - \sum_{j \neq i}\frac{\partial L}{\partial a_j}a_ia_j = a_i(\frac{\partial L}{\partial a_i} - \sum_{j=1}^{n}\frac{\partial L}{\partial a_j}a_j) ∂zi∂L=∂ai∂Lai(1−ai)−∑j=i∂aj∂Laiaj=ai(∂ai∂L−∑j=1n∂aj∂Laj)
注意到 ∑ j = 1 n ∂ L ∂ a j a j \sum_{j=1}^{n}\frac{\partial L}{\partial a_j}a_j ∑j=1n∂aj∂Laj是标量对向量的导数,它等于标量对向量各个元素的导数之和乘以向量的各个元素,即:
∑ j = 1 n ∂ L ∂ a j a j = a T ∂ L ∂ a \sum_{j=1}^{n}\frac{\partial L}{\partial a_j}a_j = \mathbf{a}^T\frac{\partial L}{\partial \mathbf{a}} ∑j=1n∂aj∂Laj=aT∂a∂L
因此,我们可以将梯度 ∂ L ∂ z \frac{\partial L}{\partial \mathbf{z}} ∂z∂L表示为:
∂ L ∂ z = a ⊙ ( ∂ L ∂ a − a T ∂ L ∂ a ) \frac{\partial L}{\partial \mathbf{z}} = \mathbf{a} \odot (\frac{\partial L}{\partial \mathbf{a}} - \mathbf{a}^T\frac{\partial L}{\partial \mathbf{a}}) ∂z∂L=a⊙(∂a∂L−aT∂a∂L)
其中, ⊙ \odot ⊙表示逐元素乘法。这个公式就是Softmax层反向传播的梯度计算公式。
使用梯度下降法,权重和偏置会按照以下方式更新:
weights − = learn_rate × d L dweights \text{weights} -= \text{learn\_rate} \times \frac{\text{d} L}{\text{d} \text{weights}} weights−=learn_rate×dweightsdL
biases − = learn_rate × d L dbiases \text{biases} -= \text{learn\_rate} \times \frac{\text{d} L}{\text{d} \text{biases}} biases−=learn_rate×dbiasesdL
函数返回的是损失关于输入的梯度,即 d L dinputs \frac{\text{d} L}{\text{d} \text{inputs}} dinputsdL。这个梯度可以用于更新下一层的权重和偏置。
代码详解
def backprop(self, d_L_d_out, learn_rate):
接受两个参数:d_L_d_out 和 learn_rate。d_L_d_out 是上一层传下来的梯度,而 learn_rate 是学习率,用于更新权重和偏置。
寻找非零梯度
for i, gradient in enumerate(d_L_d_out):
if gradient == 0:
continue
这个循环遍历传入的梯度 d_L_d_out。由于 softmax 层的特性,通常只有一个元素的梯度是非零的。找到这个非零元素并进行处理。
计算 e 的 totals 次方
t_exp = np.exp(self.last_totals)
这里,self.last_totals 是 softmax 层输入(即上一层的输出)的累加和。这行代码计算了 e 的 self.last_totals 次方。
计算 S,即所有 e^totals 的和
S = np.sum(t_exp)
S是所有e^totals` 的和,用于归一化,使 softmax 输出的概率之和为 1。
计算输出对 totals 的梯度
d_out_d_t = -t_exp[i] * t_exp / (S ** 2)
d_out_d_t[i] = t_exp[i] * (S - t_exp[i]) / (S ** 2)
这里计算了 softmax 函数对 totals 的偏导数。这个偏导数用于后续计算损失函数对权重、偏置和输入的梯度。
计算 totals 对权重/偏置/输入的梯度
d_t_d_w = self.last_input
d_t_d_b = 1
d_t_d_inputs = self.weights
计算了 totals 对权重(self.weights)、偏置(这里简化为 1)和输入(self.last_input)的梯度。注意这里totals 是输入和权重的线性组合,且偏置的梯度为常数 1。
计算损失对 totals 的梯度
d_L_d_t = gradient * d_out_d_t
通过链式法则计算了损失函数对 totals 的梯度。它是将上一步计算的梯度与传入的梯度相乘得到的。
计算损失对权重/偏置/输入的梯度
d_L_d_w = d_t_d_w[np.newaxis].T @ d_L_d_t[np.newaxis]
d_L_d_b = d_L_d_t * d_t_d_b
d_L_d_inputs = d_t_d_inputs @ d_L_d_t
通过链式法则和矩阵运算计算了损失函数对权重、偏置和输入的梯度。这些梯度将用于更新网络的参数。
更新权重和偏置
self.weights -= learn_rate * d_L_d_w
self.biases -= learn_rate * d_L_d_b
这里使用梯度下降法更新了权重和偏置。学习率 learn_rate 控制了参数更新的步长。
返回输入的梯度
return d_L_d_inputs.reshape(self.last_input_shape)
最后,函数返回了损失函数对输入的梯度,以便传递给前一层进行反向传播。梯度的形状被重新调整为与输入相匹配。
def backprop(self, d_L_d_out, learn_rate):
for i, gradient in enumerate(d_L_d_out):
if gradient == 0:
continue
# e^totals
t_exp = np.exp(self.last_totals)
# Sum of all e^totals
S = np.sum(t_exp)
# Gradients of out[i] against totals
d_out_d_t = -t_exp[i] * t_exp / (S ** 2)
d_out_d_t[i] = t_exp[i] * (S - t_exp[i]) / (S ** 2)
# Gradients of totals against weights/biases/input
d_t_d_w = self.last_input
d_t_d_b = 1
d_t_d_inputs = self.weights
# Gradients of loss against totals
d_L_d_t = gradient * d_out_d_t
# Gradients of loss against weights/biases/input
d_L_d_w = d_t_d_w[np.newaxis].T @ d_L_d_t[np.newaxis]
d_L_d_b = d_L_d_t * d_t_d_b
d_L_d_inputs = d_t_d_inputs @ d_L_d_t
# Update weights / biases
self.weights -= learn_rate * d_L_d_w
self.biases -= learn_rate * d_L_d_b
return d_L_d_inputs.reshape(self.last_input_shape)
训练过程
训练过程可以总结为以下几步:
- 加载数据集
- 创建需要的卷积层,池化层和Softmax层
- 通过组合各层创建前向传播序列
- 创建单个训练序列,包括执行前向传播序列,计算损失梯度,反向传播
- 根据具体情况,迭代执行训练序列
# We only use the first 1k examples of each set in the interest of time.
# Feel free to change this if you want.
train_images = mnist.train_images()[:1000]
train_labels = mnist.train_labels()[:1000]
test_images = mnist.test_images()[:1000]
test_labels = mnist.test_labels()[:1000]
conv = Conv3x3(8) # 28x28x1 -> 26x26x8
pool = MaxPool2() # 26x26x8 -> 13x13x8
softmax = Softmax(13 * 13 * 8, 10) # 13x13x8 -> 10
def forward(image, label):
'''
Completes a forward pass of the CNN and calculates the accuracy and
cross-entropy loss.
- image is a 2d numpy array
- label is a digit
'''
# We transform the image from [0, 255] to [-0.5, 0.5] to make it easier
# to work with. This is standard practice.
out = conv.forward((image / 255) - 0.5)
out = pool.forward(out)
out = softmax.forward(out)
# Calculate cross-entropy loss and accuracy. np.log() is the natural log.
loss = -np.log(out[label])
acc = 1 if np.argmax(out) == label else 0
return out, loss, acc
def train(im, label, lr=.005):
# Forward
out, loss, acc = forward(im, label)
# Calculate initial gradient
gradient = np.zeros(10)
gradient[label] = -1 / out[label]
# Backprop
gradient = softmax.backprop(gradient, lr)
gradient = pool.backprop(gradient)
gradient = conv.backprop(gradient, lr)
return loss, acc
print('MNIST CNN initialized!')
# Train the CNN for 3 epochs
for epoch in range(3):
print('--- Epoch %d ---' % (epoch + 1))
# Shuffle the training data
permutation = np.random.permutation(len(train_images))
train_images = train_images[permutation]
train_labels = train_labels[permutation]
# Train!
loss = 0
num_correct = 0
for i, (im, label) in enumerate(zip(train_images, train_labels)):
if i % 100 == 99:
print(
'[Step %d] Past 100 steps: Average Loss %.3f | Accuracy: %d%%' %
(i + 1, loss / 100, num_correct)
)
loss = 0
num_correct = 0
l, acc = train(im, label)
loss += l
num_correct += acc
测试过程
测试过程中重要的是使用测试数据集,而且测试过程中不再反向传播梯度
# Test the CNN
print('\n--- Testing the CNN ---')
loss = 0
num_correct = 0
for im, label in zip(test_images, test_labels):
_, l, acc = forward(im, label)
loss += l
num_correct += acc
num_tests = len(test_images)
print('Test Loss:', loss / num_tests)
print('Test Accuracy:', num_correct / num_tests)
完整代码下载
https://github.com/vzhou842/cnn-from-scratch?tab=readme-ov-file