线段树：
什么是线段树？
先用一个问题来引出线段树的论述：
给你一段区间，然后给你 q次询问，每次询问让你输出这个区间的最大值。
乍一看，这不是很简单吗？只需要这样这样再那样那样就好了。
nonono
如果q=1e6次呢？ 那么这就暗示你需要一个O（1）的算法来解决这道题目。
而线段树就是解决这一类问题的好方法。
那么回来了，线段树是什么？ 我们只知道线段树是一种数据结构，它能处理上面的问题。还有么？
其实，线段树的用途很广泛，他能作用大多数的区间查询问题。
例如求区间和、求区间最值、求区间内满足某种条件的元素个数等等。
你可能已经迫不及待地想要学习线段树了。
我们先抛开线段树这三个字。对于上面的问题，我们可以这样思考：
由于询问次数高达1e6次方，所以必须使用O（1）的算法。
这也就意味着，我们必须对这个问题进行预处理。只有这样我们才能在每次询问的时候直接得到答案。
假设num[l][r] 表示的是这个区间里的最大值
单在这个区间较长的情况下，我们无法将答案预处理到一个二维数组里面
因为空间复杂度将爆炸。
所以我们可以构建一个函数，这个函数的参数有我们需要查询的左右两个端点。返回值就是这个区间的最大值。
然后每次调用函数能以非常短的次数得到答案。
ok，现在的问题就是，怎么用很低的时间复杂度找到某一区间内的最大值呢？
对，没错就是二分。
一个区间的最大值，取决于 这个区间左半边的最大值，和区间右半边的最大值
然后一直递归下去，直到边界，也就是这个区间长度为1.
因为： “每一个单位长度为1的区间，其最大值就是本身。”
递归到边界之后，直接返回边界值，然后根据刚刚说的：
“ 这个区间的最大值，取决于 这个区间左半边的最大值，和区间右半边的最大值 ”
最后将每个区间的最大值存入一个数组。。。。
于是。。。
神乎其技！ 我们有了这整个线段的最大值。
其实我们仔细看看这个思路，会发现，哎哟我去，这不是分治吗。或者是：哎哟我去，这不是二叉树吗。
是的，于是我们可以用二叉树来完成上面的操作：
- 首先构建一颗二叉树，二叉树的每个结点表示一段区间。而叶子结点就表示一个个长度是1的区间，再上一层就是长度为2的区间。。。以此类推（类似这样）
[1,8] (最大值: 8)
/ \
[1,4] [5,8]
(最大值: 4) (最大值: 8)
/ \ / \
[1,2] [3,4] [5,6] [7,8]
(2) (4) (6) (8)
- 然后写一个查询函数，search（当前结点编号，当前结点编号对应区间，需要查询的区间）
这就是经典的二分了，查询这个区间是在哪个结点处，如果这个区间能把当前结点对应的区间包含住，那么我们直接返回这个结点的值就可以了。
否则的话，根据这个区间出现在左半边还是右半边进行二分查找即可
（有人可能会问，如果这个区间，出现在结点区间的中间怎么办）
（ps：黄色是目标区间，红色是当前结点区间，绿色是二分的位置。）
难办？其实是一样的，如果在中间的话，我们还是能继续二分啊，
只不过我们继续二分的话，会分别二分到黄色区间的左端点，和右端点。
当结点区间的左端点为目标区间的左端点的时候（结点区间的右端点是绿色处）
那么我们不就求出了左黄部分的最大值了吗。
右端点同理啊。
而一个区间的最大值不就是可以分为这个区间以某点为分界线的左边最大值和右边最大值的最大值吗？
所以就求完了啊。
而第三种情况就是，当你的目标区间和结点区间完全没有交集的时候，我们直接返回0就可以了。
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
总结一下线段树：
- 线段树是一种用于高效处理区间查询的数据结构，通常用于解决数组或线性数据结构上的区间查询问题。
- 线段树的基本思想是将一个线性的区间划分成若干个小区间，对每个小区间维护一个值，然后通过递归的方式建立一棵树状结构，使得每个节点代表一个区间，并且这些区间两两不重叠，同时完全覆盖整个线性区间。这样，就可以在每个节点上记录该区间的一些信息，比如最大值、最小值、区间和等等，以便快速地进行区间查询和更新操作。
- 线段树的建立过程和查询过程都是基于递归的思想，可以利用二叉树的结构来表示。对于一个线性区间 [l, r]，可以将其划分为 [l, m] 和 [m+1, r] 两个子区间，然后分别递归地构建左右子树，直到区间长度为1时停止递归。线段树的查询操作也是通过递归地向下搜索树的节点，并结合区间的位置关系和需要的信息进行计算得出结果。
- 线段树在解决一些区间查询问题上有着良好的效果，比如求区间最大值、最小值、区间和、区间内满足某种条件的元素个数等。
上面只是一个非常简单的线段树模板。
并且只涉及到线段树的：单点增删改查，建树过程，区间查询。
那么我们下面再讲述一个操作，就是线段树的区间更新。
例如，我们如果要将某一段区间都加上一个val值应该如何操作？
这就会用到一个很有用的技巧：lazy-tag 懒惰标记
什么意思呢？听我娓娓道来：
假如，我们要给一段指定的区间内的每个元素加上val。
那么对于线段树的结构来说（假如现在我们规定线段树的每个结点代表对应区间的和）
有人可能会想：
我们从上到下遍历，先查找出这个区间的位置。
然后直接给这个区间原来的值加上 val*区间长度 不就好了。
嗯。。。。
说的很好，但是，你这样的话是有隐患的，因为你只改变了这个区间以及这个区间以上的部分。
这个区间以下的部分你没有改变。
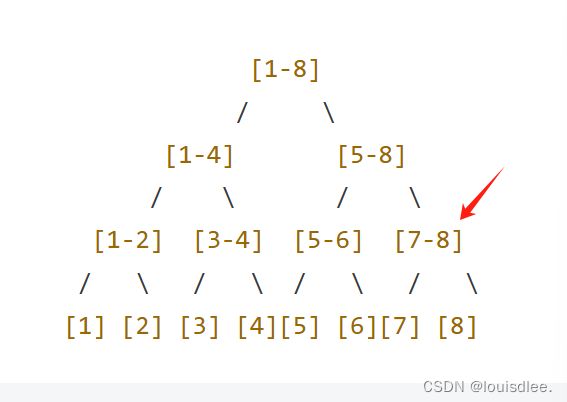
就比如，我们要给区间[7,8]里的每个数+val ， 当你找到[7,8]位置是，不会再递归下去了，所以[7],[8]这俩区间没有被加上val。说明这个算法是有错的。
那么问题又来了，我们要给每个单位区间都加上val ，那么我们就需要遍历每个结点吧。。
是的，这样的话，每次修改的时间就比较长。
ok，现在有请我们的主角！ lazy-tag
它的原理就是，给每一个打上标记的点，对其左右子节点进行某项操作，然后再把这个父节点的标记去除。
然后下次我们更新的话，只要提前查询以下这个结点是否被标记，如果被标记了，说明是之前的更新操作留下来的标记（ 留下标记代表什么？代表从这个结点之后的每个值在那一次更新操作中都需要被更新为某个值，如加上val这种）
主打的就是一个懒惰，如果之后的查询中，这段区间再也没被查到，或者这段区间的子区间再也没被查到的话，那么那个懒惰标记就永远留在那里了。。。
上模板：
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
嗯。。这个代码就是下面这道题的题解。P3372 【模板】线段树 1 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
https://www.luogu.com.cn/problem/P3372
线段树怎么做都不嫌多，再来一道吧！
P1253 扶苏的问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)https://www.luogu.com.cn/problem/P1253
这题比较有意思，篇板子一点，重要的是怎么将板子巧妙结合一下？
这道题主要让我们实现三个功能：
- 将给定区间的所有值都替换为x
- 将给定区间的所有值都加上x
- 求给定区间的最大值
虽然，三个功能的板子我们都会写，不过呢，由于懒标记的延迟性，我们执行操作1、2的时候，要考虑到顺序。
假设，我们在之前已经执行过一次替换操作了，我们现在要执行加操作，应该注意到，执行加操作应该是在替换操作的基础上执行的。
先判断这一层有没有替换操作的懒标记，如果有，我们就要先进行替换操作，然后再进行加操作。
那么假设我们执行加操作之后，又需要执行替换操作。我们是否要像前面一样判断是否加操作的标记呢?
实际上是不需要的，如果这一层需要既被加操作标记了，而后又需要进行替换操作，我们直接将加操作标记清除即可。
然后再维护最大值就好了。
然后这道题，注意要开long long。
并且，这道题还有一些很坑的数据点！
首先，x可以取0，和0以下的值。 那么替换操作的懒标记就不能初始化为0.
要不然就忽视了将区间数全部替换为0的情况。
并且，还能替换成负数。这个是值得注意的。
然后，加操作的懒标记是不需要改的，0就相当于没加。
还有一定要记得！！！开longlong！！！特么的，我没开longlong被卡了两三个小时。
嗯，然后记得写快读，或者关同步流。。。
（警钟长鸣！！！我宏定义了一个常量叫node，然后写了一个函数叫research。。。然后疯狂报错，调了半天才知道撞定义了）
下面上代码：
#define _CRT_SECURE_NO_WARNINGS //禁用警告
#include //输入输出流库
#include //C风格输入输出库
#include //数学函数库
#include //字符串库
#include //C风格字符串库
#include //常用算法库
#include //向量库
#include //字符处理库
#include
