图的存储方式合集

前言

图的存储结构相较线性表与树来说较为复杂，因而对于不同情况需要不同的存储策略。本文就几种常见的存图结构展开介绍。

---

邻接矩阵

由于图由顶点和边组成，顶点可以由一维数组存储，点与点之间的关系仅靠一维难以表示，所以考虑二维存储，邻接矩阵由此诞生。

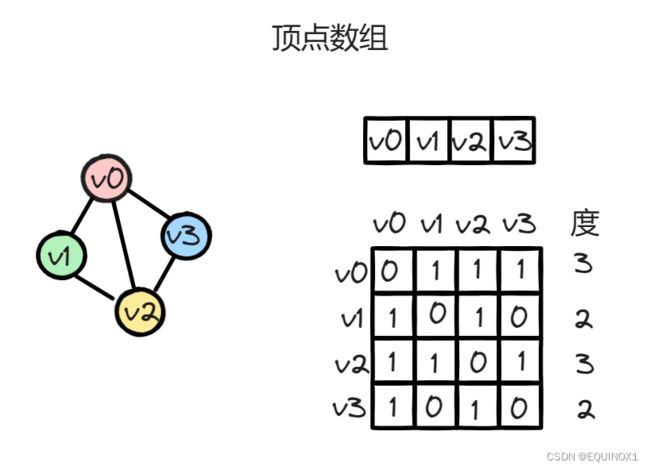
图的**邻接矩阵( Adjacency Matrix)**存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。

无权图

设G(V,E)有n个顶点，V,E分别为顶点集合和边集合，邻接矩阵grid为n*n方阵，则有：
$$grid[i][j]\{\begin{array}{c}1，<i,j>\in E\\ 0,其它\end{array}$$
无向图示例，每个节点的度为对应行求和。

有向图示例，入度为对应行求和，出度为对应列求和

带权图

对于带权图而言，邻接矩阵中的值变为了对应边的权值，通常情况下用无穷来表示两点间无边。

设G(V,E)有n个顶点，V,E分别为顶点集合和边集合，邻接矩阵grid为n*n方阵，则有：
$$grid[i][j]\{\begin{array}{c}{w}_{ij}，<i,j>\in E\\ 0,i=j\\ \infty ,其他\end{array}$$

由于邻接矩阵代码实现十分简单一个二维数组即可，就不给出代码实现了。

---

邻接表

邻接矩阵是不错的一种图存储结构，但是我们也发现，对于边数相对顶点较少的图，这种结构是存在对存储空间的极大浪费的。比如说，如果我们要处理下图这样的稀疏有向图，邻接矩阵中除了grid[0][1]有权值外，没有其他弧，其实这些存储空间都浪费掉了。

因此我们考虑另外一种存储结构方式。回忆我们在学习线性表时谈到，顺序存储结构就存在预先分配内存可能造成存储空间浪费的问题，于是引出了链式存储的结构。同样的，我们也可以考虑对边或弧使用链式存储的方式来避免空间浪费的问题。

我们在学习树这一数据结构的时候了解过孩子表示法，即将节点存入数组并对节点的孩子进行链式存储，那么不管有多少孩子都不会存在空间浪费，我们图中也可以用这种存储方式，我们将这种数组和链表结合的存储方法称为邻接表（Adjacency List）。

邻接表处理方法如下：

• 图中的节点都用一维数组存储或者单链表存储，只不过数组的随机访问更便于我们读取顶点信息，数组中每个数据元素为指向对应顶点第一个邻接点的指针。
• 每个顶点和其邻接点构成一个线性表，由于邻接点个数不定，所以采用单链表存储。

如下图就是一个无向图的邻接表结构：

边节点定义

代码实现如下：

#define N 10010//最大顶点数目

struct edge
{
    edge(int u = 0, int v = 0, int w = 0, edge *next = nullptr) : _u(u), _v(v), _w(w), _next(next) {}
    int _u; // 顶点
    int _v; // 邻接点
    int _w; // 权值
    edge *_next;
};
vector AdjList(N); // 邻接表

边的添加

对于添加边的过程就是在单链表中添加节点的过程，我们可以在任何位置添加，由于我们邻接表中存储了表头指针，所以我们可以在O(1)的时间复杂度内添加节点，也就是说，边的添加其实就是一个链表头插的过程。

代码实现如下：

void addedge(int u, int v, int w)
{
    AdjList[u] = new edge(u, v, w, AdjList[u]);
}

邻接表的建立

那么给定若干节点和边，我们只需要按部就班地进行边的插入即可。

int n; // 顶点数目
void create()
{
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        int u, v, w; // 无权图可以只读顶点和邻接点
        cin >> u >> v >> w;
        addedge(u, v, w);
    }
}

---

十字链表

对于有向图而言，我们很多时候会关心顶点的出度入度问题，那么对于有向图建立邻接表后，我们可以轻松的得到某个点的出度，那么我们如果想要知道某个点的入度难道要暴力的遍历整个邻接表吗？这显然不划算，不过我们可以建立一个逆邻接表，这样就解决了出度入度问题，不过我们是否可以更进一步，将二者整合为一个数据结构呢？当然可以，这就是图的另一种存储方式——十字链表（Orthogonal List）。

我们学习过单向链表，双向链表、双向循环链表，其中思维难度并没有什么飞跃，十字链表也是一样。

原先的正向邻接表中每个位置存放的是对应顶点的出边链表表头指针，逆向邻接表中每个位置存放的是对应顶点的入边链表表头指针，那么我们直接在每个位置存放对应顶点的出边链表表头指针和入边链表表头指针就有了十字链表的基本框架（什么缝合怪

十字链表定义

十字链表基本框架如下：

class OrthogonalList
{
public:
    OrthogonalList(int n) : OrList(n) // 节点0~n
    {
    }

    void addedge(int u, int v, int w);

private:
    vector OrList;//顶点表
};

顶点表节点定义

我们之前直接在顶点表每个位置存放一个指针，现在要存放两个指针，当然要对其进行封装。

struct Node
{
    edge *firstin = nullptr;  // 入边链表表头
    edge *firstout = nullptr; // 出边链表表头
};

边节点定义

根据十字链表的要求呢我们对于边我们既能从该边找到下一条由u发出的边又能要找到下一条指向v的边，则有如下结构：

struct edge
{
    edge(int u = 0, int v = 0, int w = 0, edge *outnext = nullptr, edge *innext = nullptr)
        : _u(u), _v(v), _w(w), _outnext(outnext), _innext(innext) {}
    int _u;         // 顶点
    int _v;         // 邻接点
    int _w;         // 权值
    edge *_outnext; // 边起点相同的链表指针
    edge *_innext;  // 边终点相同的链表指针
};

边的添加

整体的添加逻辑和邻接表类似，由原先的一个头插变为了现在的两个头插

    void addedge(int u, int v, int w)
    {
        OrList[u].firstout = new edge(u, v, w, OrList[u].firstout, OrList[v].firstin);
        OrList[v].firstin = OrList[u].firstout;
    }

---

邻接多重表

我们前面似乎一直在讲存图，添边，没有涉及到删边，改边，对于我们的邻接表结构，如果我们存储的是有向图，那么删除一条边最坏情况下要遍历整条出边链表，如果是无向图那最坏情况就要遍历一条出边链表一条入边链表，这是链式存储结构不可避免的问题，对于有向图而言，似乎还可以接受，那么对于无向图而言有没有什么优化手段呢？

我们发现对于邻接表存储无向图之所以删除一条边要进行两次遍历就在于我们找到了却无法直接找到

我们可以通过某种手段使得二者可以互相抵达，似乎可以解决问题，但是我们也可以仿照十字链表那样，修改边节点的结构，拓展边与边之间的关系，这就引出了当边成为了关注重点时，对于无向图存图的优化策略——邻接多重表(Ajacency Multilist)。

边节点定义

对于邻接表存无向图，实际上是存了的同时又存了，我们其实可以用同一条边分别给两条边链表使用，和十字链表一样，同样要两个指针域。

struct edge
{
    edge(int u = 0, int v = 0, int w = 0, edge *unext = nullptr, edge *vnext = nullptr)
        : _u(u), _v(v), _w(w), _unext(unext), _vnext(vnext) {}
    int _u;       // 顶点
    int _v;       // 邻接点
    int _w;       // 权值
    edge *_unext; // 和u相连的下一条边
    edge *_vnext; // 和v相连的下一条边
};

邻接多重表定义

基本框架如下：

class MultiAList
{
public:
    MultiAList(int n) : maList(n) // 节点0~n
    {}

    void addedge(int u, int v, int w)
    {}
    
    bool deledge(int u ,int v)
    {}

private:
    vector maList;
};

边的添加

仍然是很简约的链表头插，相较于邻接表存无向图，这里我们只用了一条边但是拿给了两条链用

    void addedge(int u, int v, int w)
    {
        edge *newedge = new edge(u, v, w, maList[u], maList[v]);
        maList[u] = maList[v] = newedge;
    }

边的删除

对于待删除边（亦即）我们从u，v任意的出边链表选取表头，因为它们两个的表头是一样的，不妨选定u的边链表，注意我们对于一个边节点而言要对_u和_v中哪一个和u相同进行判断，从而判断下一步往哪走

和一般的单链表删除相同，注意特判头节点

代码逻辑就是正常的链表删除逻辑

    bool deledge(int u, int v)
    {
        edge *cur = maList[u], *pre = nullptr;
        while (cur)
            if ((u == cur->_u ? cur->_v : cur->_u) == v)
                break;
            else
            {
                pre = cur;
                cur = u == cur->_u ? cur->_unext : cur->_vnext;
            }
        if (!cur) // 没找到对应边，删除失败
            return false;
        if (pre)
        {
            pre->_unext = pre->_u == cur->_u ? cur->_unext : cur->_vnext;
            pre->_vnext = pre->_v == cur->_v ? cur->_vnext : cur->_unext;
        }
        if (maList[u] == cur)
            maList[u] = cur->_u == u ? cur->_unext : cur->_vnext;
        if (maList[v] == cur)
            maList[v] = cur->_v == v ? cur->_vnext : cur->_unext;
        delete cur;
        return true;
    }

邻接多重表和邻接表区别就是一条边和两条边的区别。

---

三元组表

**三元组表（Three tuple）**其实是针对稀疏矩阵的优化存储方式，当然也可以归到图的存储之中。

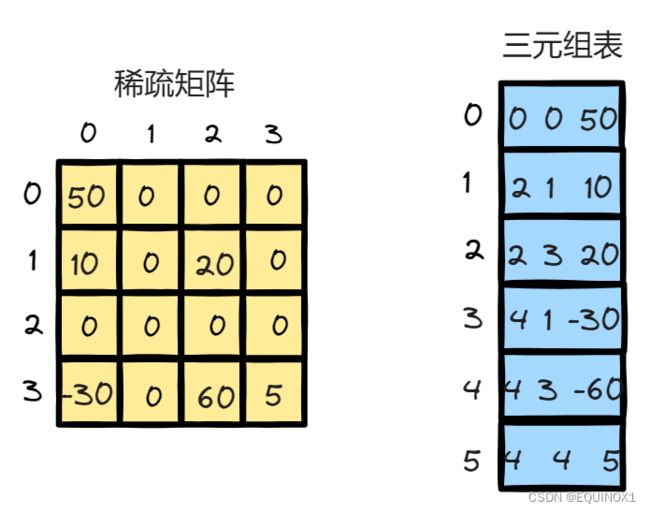
对于稀疏矩阵而言，其中只有稀少的有效元素，那么对于大部分矩阵空间是冗余的，换句话说，我们只需要存储那些有效元素即可。

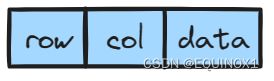
将表示稀疏矩阵的非零元素的三元组结点按行优先的顺序排列，得到-一个线性表，将此线性表用顺序存储结构进行存储，称之为三元组表（Three tuple）。

节点设计

struct Node
{
    Node(int row, int col, int data) : _row(row), _col(col), _data(data) {}
    int _row, _col, _data;//行号、列号、数据
};

矩阵矩阵的三元组表表示

三元组表将原稀疏矩阵的有效元素按照按行优先进行存放，从而得到了一个线性表。

class ThreeTable
{
public:
    ThreeTable() = default;
    ThreeTable(int t) : table(t) {}
    ThreeTable(vector> matrix);//矩阵转三元组表
    ThreeTable transpose();//转置
    void display();

private:
    vector table;
    int _m, _n;
};

朴素三元组表矩阵转置

那么三元组表如何进行矩阵转置并存到另一个三元组表中呢？

朴素转置算法：

• 从0开始枚举列号，新三元组表b，b的待添加下标k

• 每枚举列号i，都对原三元组表a进行遍历

• 如果a[j]的列号为i，那么把a[j]行列号对换放到b[j]，j++

• 时间复杂度：O（n * U），n为列数，U为三元组表的元素个数

代码如下：

    ThreeTable transpose()
    {
        ThreeTable b;
        for (int i = 0, t = table.size(); i < _n; i++)
        {
            for (int j = 0; j < t; j++)
            {
                if (table[j]._col == i)
                    b.table.emplace_back(table[j]._col, table[j]._row, table[j]._data);
            }
        }
        return b;
    }

快速三元组表矩阵转置

我们上面的算法效率过于低下，实际上我们可以利用桶排序的思想在O(U)内完成转置。

快速三元组表转置：

• 建立长度为n + 1桶数组bucket，bucket[i]为列号i - 1的元素个数
• 对bucket求前缀和，那么转置后处于第i行元素在b中的起始存放位置为bucket[i - 1]

代码如下：

    ThreeTable transpose()
    {
        ThreeTable b(table.size(), _n, _m);
        vector bucket(_n + 1);
        for (auto &x : table)
            bucket[x._col + 1]++;
        for (int i = 1; i < bucket.size(); i++)
            bucket[i] += bucket[i - 1];
        for (auto &x : table)
            b.table[bucket[x._col]++] = {x._col, x._row, x._data};
        return b;
    }

舞蹈链

舞蹈链（Dancing Links）其实就是双向十字循环链表，由于每个节点可以与四个方向上的节点互相访问，从而可以便于实现删除，撤销删除，基于回溯算法，舞蹈链常被用于解决精确覆盖问题和重复覆盖问题之中，详见：舞蹈链，DLX算法详解，OJ精讲，详细代码-CSDN博客

边集数组

边集数组我们在LeetCode图论相关题目中经常以参数遇到，就是一个存储边的信息的数组，边数组每个数据元素由一条边的起点下标(begin)、终点下标(end)和权值(weight)组成，如下图所示。显然边集数组关注的是边的集合，在边集数组中要查找一个顶点的度需要扫描整个边数组，效率并不高。因此它更适合对边依次进行处理的操作，而不适合对顶点相关的操作。由于边集数组很简单，我们就不过多赘述。

链式前向星

由于邻接表有扩容开销，所以在OJ中我们存图常用链式前向星，其详解在博主另一篇超详细博客中有详细讲解：一种实用的边的存储结构–链式前向星-CSDN博客