C语言数据结构课程设计 一元稀疏多项式计算器
一元稀疏多项式计算器
问题描述
设置一个一元稀疏多项式简单计算器,能够实现多项式相加减,并计算多项式a,b在x处的值。
需求分析
(1)输入并建立多项式。
(2)输出多项式,输出形式为整数序列:n,c1,e1,c2,e2,...,cn,en,其中n是多项式的项数,ci,ei,分别是第i项的系数和指数,序列按指数降序排序。
(3)实现多项式a和b相加,建立多项式a+b。
(4)实现多项式a和b相减,建立多项式a-b。
(5)计算多项式在x处的值。
算法设计和实现
- 功能图
(2)概要设计
void inputPolynomial(Polynomial* poly)// 输入多项式
void outputPolynomial(Polynomial* poly)// 输出多项式
int compare(const void* a, const void* b)// 排序函数(按指数降序)
void sortPolynomial(Polynomial* poly)// 对多项式进行排序(按指数降序)
Polynomial addPolynomial(Polynomial a, Polynomial b)// 多项式 a + b
Polynomial subtractPolynomial(Polynomial a, Polynomial b) // 多项式 a - b
int evaluatePolynomial(Polynomial* poly, int x)// 计算多项式在x处的值
(3)存储结构
typedef struct {
int coef; // 系数
int exp; // 指数
} Term;
typedef struct
{
Term terms[MAX_TERMS]; // 多项式的项数组
int numTerms; // 多项式的项数
} Polynomial;
(4)源代码
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#define MAX_TERMS 100
typedef struct {
int coef; // 系数
int exp; // 指数
} Term;
typedef struct {
Term terms[MAX_TERMS]; // 多项式的项数组
int numTerms; // 多项式的项数
} Polynomial;
// 输入多项式
void inputPolynomial(Polynomial* poly) {
printf("请输入多项式的项数:");
scanf_s("%d", &(poly->numTerms));
for (int i = 0; i < poly->numTerms; i++) {
printf("请输入第%d项的系数和指数(以空格分隔):", i + 1);
scanf_s("%d %d", &(poly->terms[i].coef), &(poly->terms[i].exp));
}
}
// 输出多项式
void outputPolynomial(Polynomial* poly) {
printf("输出多项式的整数序列:");
for (int i = 0; i < poly->numTerms; i++) {
printf("%d %d ", poly->terms[i].coef, poly->terms[i].exp);
}
printf("\n");
}
// 排序函数(按指数降序)
int compare(const void* a, const void* b) {
return ((Term*)b)->exp - ((Term*)a)->exp;
}
// 对多项式进行排序(按指数降序)
void sortPolynomial(Polynomial* poly) {
qsort(poly->terms, poly->numTerms, sizeof(Term), compare);
}
// 相加多项式 a + b
Polynomial addPolynomial(Polynomial a, Polynomial b) {
Polynomial result;
int i = 0, j = 0, k = 0;
while (i < a.numTerms && j < b.numTerms) {
if (a.terms[i].exp > b.terms[j].exp) {
result.terms[k++] = a.terms[i++];
}
else if (a.terms[i].exp < b.terms[j].exp) {
result.terms[k++] = b.terms[j++];
}
else {
int sum = a.terms[i].coef + b.terms[j].coef;
if (sum != 0) {
result.terms[k].coef = sum;
result.terms[k++].exp = a.terms[i].exp;
}
i++;
j++;
}
}
// 复制剩余的项
for (; i < a.numTerms; i++) {
result.terms[k++] = a.terms[i];
}
for (; j < b.numTerms; j++) {
result.terms[k++] = b.terms[j];
}
result.numTerms = k;
return result;
}
// 相减多项式 a - b
Polynomial subtractPolynomial(Polynomial a, Polynomial b) {
Polynomial result;
int i = 0, j = 0, k = 0;
while (i < a.numTerms && j < b.numTerms) {
if (a.terms[i].exp > b.terms[j].exp) {
result.terms[k++] = a.terms[i++];
}
else if (a.terms[i].exp < b.terms[j].exp) {
result.terms[k].coef = -b.terms[j].coef;
result.terms[k++].exp = b.terms[j++].exp;
}
else {
int diff = a.terms[i].coef - b.terms[j].coef;
if (diff != 0) {
result.terms[k].coef = diff;
result.terms[k++].exp = a.terms[i].exp;
}
i++;
j++;
}
}
// 复制剩余的项
for (; i < a.numTerms; i++) {
result.terms[k++] = a.terms[i];
}
for (; j < b.numTerms; j++) {
result.terms[k].coef = -b.terms[j].coef;
result.terms[k++].exp = b.terms[j].exp;
}
result.numTerms = k;
return result;
}
// 计算多项式在x处的值
int evaluatePolynomial(Polynomial* poly, int x) {
int result = 0;
for (int i = 0; i < poly->numTerms; i++) {
int termValue = 1;
for (int j = 0; j < poly->terms[i].exp; j++) {
termValue *= x;
}
result += poly->terms[i].coef * termValue;
}
return result;
}
// 程序入口
int main()
{
Polynomial a, b, sum, diff;
int x;
printf("=== 一元稀疏多项式简单计算器 ===\n");
// 输入多项式a和b
printf("请输入多项式 a:\n");
inputPolynomial(&a);
printf("请输入多项式 b:\n");
inputPolynomial(&b);
// 输出多项式a和b
printf("\n多项式 a:");
outputPolynomial(&a);
printf("多项式 b:");
outputPolynomial(&b);
// 对多项式a和b进行排序
sortPolynomial(&a);
sortPolynomial(&b);
// 相加多项式a和b
sum = addPolynomial(a, b);
printf("\na + b:");
outputPolynomial(&sum);
// 相减多项式a和b
diff = subtractPolynomial(a, b);
printf("a - b:");
outputPolynomial(&diff);
// 计算多项式在x处的值
printf("\n请输入 x 的值:");
scanf_s("%d", &x);
int value = evaluatePolynomial(&a, x);
printf("多项式 a 在 x=%d 处的值为:%d\n", x, value);
value = evaluatePolynomial(&b, x);
printf("多项式 b 在 x=%d 处的值为:%d\n", x, value);
return 0;
} 2.1.4调试分析与测试结果
(1)问题
现象:"error C4996: 'scanf': This function or variable may be unsafe. Consider using scanf_s instead. To disable deprecation, "_CRT_SECURE_NO_WARNINGS". See online help for details."
原因:scanf函数在VS中报错的主要原因是 scanf被认为不安全而被编译器默认设置为禁用。
方法:将scanf改为scanf_s,但是这需要一个个的改,太麻烦,所以可以在代码最顶端输入#define _CRT_SECURE_NO_WARNINGS即可。
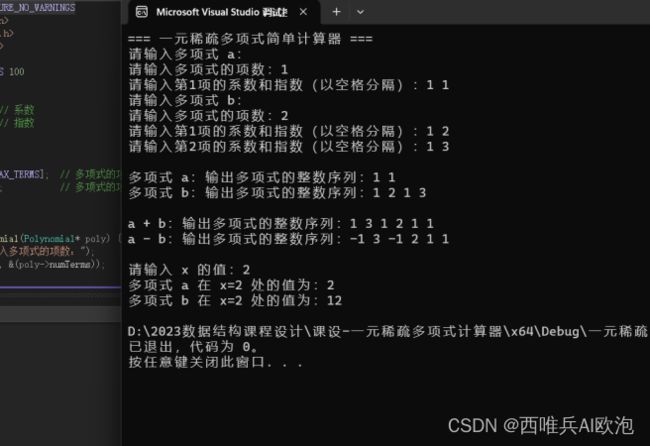
(2)运行结果
输入多项式a为x,输入多项式b为x^2+x^3。a+b=x^3+x^2+x,整数序列为1,3,1,2,1,1。a-b=-x^3-x^2+x,整数序列为-1,3,-1,2,1,1。当x=2时,a=2,b=12。所得运行结果正确。