【人工智能Ⅰ】实验11：支持向量机

实验11 支持向量机

一、实验目的

1：了解支持向量机的结构和原理。

2：应用支持向量机建立训练模型，对模型进行评估。

二、实验内容和要求

【实验内容】

选择支持向量机，对花卉图像或玉米果穗图像进行分类。花卉图像包括玫瑰，向日葵和蒲公英；玉米果穗图像包括虫蛀，损伤，发霉。

（1）可针对这些特点对图像的颜色、纹理、形状进行分析，从而进行特征选择与提取；

（2）也可以尝试不提取特征，直接将图像作为输入，对比效果；

（3）调整人工神经网络的参数，观察不同的参数对分类结果的影响；

（4）实现对花卉图像的分类。

【实验要求】

1：完成对花卉数据集的分类任务。

2：调整不同的参数，通过对分类结果的对比，选取合适的参数。

3：使用不同的样本数量，查看是否对分类结果产生影响。可对样本进行扩增（例如：反转、平移、缩放、亮度变化）。

4：进行人工神经网络和支持向量机的方法对比。

三、实验结果与分析

1：基于sklearn依赖的SVM多分类

【1】代码任务解析：

（1）初始化数据集路径和分类标签

（2）读取数据集图像信息

（3）将图像提取的像素转成numpy数组

（4）按照8：2的比例划分训练集和测试集

（5）调用sklearn中的SVM-Classifier，实例化模型

（6）输入训练集进行训练，并输出训练集的准确率

（7）输入测试集进行预测，并输出测试集的准确率

【2】程序输出结果：

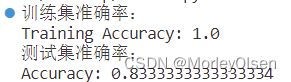
上述程序打印了SVM多分类的训练集准确率和测试集准确率，在花卉数据集上的结果如下图所示。

在玉米数据集上的结果如下图所示。

综上所述，在花卉数据集上SVM的训练集准确率是1.00、测试集准确率是0.83；在玉米数据集上SVM的训练集准确率是1.00、测试集准确率是0.50。

2：基于数学原理手动实现的SVM多分类代码

【1】代码任务解析：

（1）构建SimpleSVM类，定义初始化函数init、训练函数fit（包含损失曲线的绘制）、预测函数predict，各个函数的代码如下图所示。

init函数：

fit函数：

predict函数：

（2）读取数据集图像信息

（3）将图像提取的像素转成numpy数组

（4）按照8：2的比例划分训练集和测试集
（5）调用SimpleSVM类，实例化模型

（6）输入训练集进行训练，并输出训练集的准确率

（7）输入测试集进行预测，并输出测试集的准确率

（8）从测试集中随机抽样，输出真实标签和预测标签

【2】程序输出结果：

上述程序在训练过程中跟踪了模型的损失，并绘制出了损失曲线。在花卉数据集上的结果如下图所示。可以发现，随着迭代次数epoch的增加，模型的损失loss在逐渐稳定。

SVM模型训练完成后，计算了训练集准确率和测试集准确率，结果如下图所示。

综上所述，在花卉数据集上SVM的训练集准确率是1.00、测试集准确率是0.67。

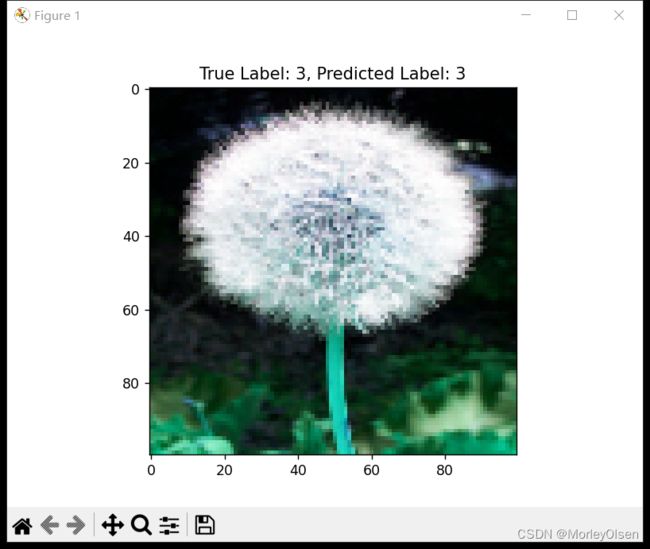
同时，上述程序中展示了模型的预测性能，对5张测试集图像进行了抽样展示，结果如下图所示。

【测试1：真实标签——2，预测标签——2，二者相同】

【测试2：真实标签——1，预测标签——1，二者相同】

【测试3：真实标签——3，预测标签——3，二者相同】

【测试4：真实标签——2，预测标签——2，二者相同】

【测试5：真实标签——2，预测标签——3，二者不相同】

3：进行人工神经网络和支持向量机的方法对比

在这两次的实验过程中，从训练过程来看，SVM的训练速度明显优于ANN的训练速度，且SVM的模型参数明显少于ANN的模型参数。从训练结果来看，SVM的准确率明显高于ANN的准确率。

同时，当ANN在训练集上表现出较高的准确率时，往往会在测试集上表现不佳，这表明模型存在过拟合问题。而支持向量机通常具有更好的泛化能力，对过拟合的抵抗能力较强。

综上所述，两种方法的对比总结如下。

（1）学习方式：

ANN：人工神经网络是一种基于神经元模型的机器学习方法，通过前向传播和反向传播来学习权重和参数，是一种端到端的学习方法，可以适应各种不同的任务。

SVM：支持向量机是一种监督学习方法，它寻找一个最优的超平面来分隔不同类别的数据点，是一种判别式学习方法，主要用于分类问题。

（2）可解释性：

ANN：神经网络通常被认为是黑盒模型，难以解释其内部的决策过程。

SVM：支持向量机的决策边界由支持向量确定，相对较容易解释和可视化。

（3）计算复杂度：

ANN：神经网络通常需要更多的计算资源和时间来训练。

SVM：支持向量机通常具有较低的计算复杂度，例如线性核情况。

（4）鲁棒性：

ANN：神经网络对于数据中的噪声和异常值较为敏感，需要大量数据来训练稳定的模型。

SVM：支持向量机对异常值有一定的鲁棒性，主要依赖于支持向量来确定决策边界。

（5）参数调整：

ANN：神经网络通常有很多参数需要调整，包括层数、神经元数量、学习率、激活函数等。

SVM：支持向量机的参数通常较少，主要是正则化参数C和核函数的选择。

4：基于实验指导的SVM模型实现（针对mnist手写数据集）

【1】代码任务解析：

（1）将csv文件转化为npy文件

（2）修改SVM代码中main函数部

【2】程序输出结果：

四、遇到的问题和解决方法

问题1：在针对图像数据集运行实验指导中提供的代码时，实例化模型会出现以下的报错。

解决1：未解决，如果对矩阵进行flatten（平整化），则会继续出现dim不符合的报错。最后直接重新实现了新的代码，如SimpleSVM类所示。

五、实验总结

1：SVM是一种有监督学习算法，能够找到在高维空间中有效分隔不同类别的超平面，在高维问题中表现出色，适用于处理具有大量特征的数据集。SVM对异常值具有一定的鲁棒性，因为它主要依赖于支持向量来确定超平面，而不是全部数据点。同时，SVM有一些参数需要调整，如正则化参数C、核函数的类型和参数等。

2： SVM最初是用于二元分类问题的，但也可以通过一对多（One-vs-Rest，OvR）或一对一（One-vs-One，OvO）等策略扩展到多元分类问题。

3：最大间隔：能够最大化两个不同类别之间的间隔的超平面。最大间隔有助于提高模型的泛化性能。

4：SVM可以使用核函数来处理非线性可分的数据。常用的核函数包括线性核、多项式核和径向基函数（RBF）核。

六、程序源代码

1：基于sklearn依赖的SVM多分类代码

import os import numpy as np import cv2 from sklearn.model_selection import train_test_split from sklearn.svm import SVC from sklearn.metrics import accuracy_score # 图像数据所在的根目录 data_root = r'C:\Users\86158\Desktop\dataset\data1' # 遍历每个类别的文件夹 class_labels = [] X = [] y = [] for class_label in os.listdir(data_root):     class_path = os.path.join(data_root, class_label)         # 确保当前路径是一个目录     if os.path.isdir(class_path):         class_labels.append(class_label)                 # 分配一个唯一的整数标签给每个类别         label = len(class_labels) - 1                   # 遍历当前类别的图像文件         for image_file in os.listdir(class_path):             image_path = os.path.join(class_path, image_file)                         # 使用OpenCV加载图像             image = cv2.imread(image_path)                         # 调整图像大小为统一的尺寸 100x100             image = cv2.resize(image, (100, 100))                         # 展平图像数据             image_flat = image.flatten()                         # 将图像数据和标签添加到X和y中             X.append(image_flat)             y.append(label) # 将图像数据转换为NumPy数组 X = np.array(X) y = np.array(y) # 数据集划分为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 创建SVM分类器 svm_classifier = SVC(kernel='linear', C=1.0, random_state=42) # 训练分类器 svm_classifier.fit(X_train, y_train) # 在训练集上进行预测 y_train_pred = svm_classifier.predict(X_train) # 计算训练集准确率 train_accuracy = accuracy_score(y_train, y_train_pred) print("训练集准确率：") print(f'Training Accuracy: {train_accuracy}') # 在测试集上进行预测 y_pred = svm_classifier.predict(X_test) # 计算准确率 accuracy = accuracy_score(y_test, y_pred) print("测试集准确率：") print(f'Accuracy: {accuracy}')

2：基于数学原理手动实现的SVM多分类代码

import numpy as np import os import cv2 from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score import matplotlib.pyplot as plt import random class SimpleSVM:     def __init__(self):         self.weights = None         self.classes = None     def fit(self, X, y, epochs=100, lr=0.001, lambda_param=0.01):         self.classes = np.unique(y)         n_samples, n_features = X.shape         n_classes = len(self.classes)         # 初始化权重         self.weights = np.zeros((n_classes, n_features))         # 训练过程         for _ in range(epochs):             for idx, x_i in enumerate(X):                 class_index = np.where(self.classes == y[idx])[0][0]                 for c in range(n_classes):                     if c == class_index:                         continue                     margin = 1 - np.dot(x_i, self.weights[class_index]) + np.dot(x_i, self.weights[c])                     if margin > 0:                         self.weights[class_index] -= lr * (-2 * lambda_param * self.weights[class_index] - x_i)                         self.weights[c] -= lr * (-2 * lambda_param * self.weights[c] + x_i)     def predict(self, X):         predictions = np.dot(X, self.weights.T)         return self.classes[np.argmax(predictions, axis=1)]         # 重新定义fit函数，在训练过程中输出loss     def fit(self, X, y, epochs=100, lr=0.001, lambda_param=0.01):         self.classes = np.unique(y)         n_samples, n_features = X.shape         n_classes = len(self.classes)         # 初始化权重         self.weights = np.zeros((n_classes, n_features))                 # 用于存储损失值         losses = []         # 训练过程         for epoch in range(epochs):             for idx, x_i in enumerate(X):                 class_index = np.where(self.classes == y[idx])[0][0]                 for c in range(n_classes):                     if c == class_index:                         continue                     margin = 1 - np.dot(x_i, self.weights[class_index]) + np.dot(x_i, self.weights[c])                     if margin > 0:                         self.weights[class_index] -= lr * (-2 * lambda_param * self.weights[class_index] - x_i)                         self.weights[c] -= lr * (-2 * lambda_param * self.weights[c] + x_i)                         # 计算损失并添加到列表中             loss = 0.5 * np.sum(self.weights ** 2) + np.sum(np.maximum(0, 1 - np.dot(X, self.weights.T)))             losses.append(loss)                 # 绘制损失曲线         plt.plot(range(1, epochs + 1), losses, marker='o')         plt.xlabel('Epochs')         plt.ylabel('Loss')         plt.title('Loss Curve')         plt.show() data_root = r'C:\Users\86158\Desktop\dataset\data1' # 遍历每个类别的文件夹 class_labels = [] X = [] y = [] for class_label in os.listdir(data_root):     class_path = os.path.join(data_root, class_label)         # 确保当前路径是一个目录     if os.path.isdir(class_path):         class_labels.append(class_label)         label = len(class_labels) - 1  # 分配一个唯一的整数标签给每个类别                 # 遍历当前类别的图像文件         for image_file in os.listdir(class_path):             image_path = os.path.join(class_path, image_file)                         # 使用OpenCV加载图像             image = cv2.imread(image_path)                         # 调整图像大小为统一的尺寸 100x100             image = cv2.resize(image, (100, 100))                         # 展平图像数据             image_flat = image.flatten()                         # 将图像数据和标签添加到X和y中             X.append(image_flat)             y.append(label) # 将图像数据转换为NumPy数组 X = np.array(X) y = np.array(y) # 数据集划分为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) model = SimpleSVM() model.fit(X_train,y_train) y_pred = model.predict(X_test) # 计算准确率 accuracy = accuracy_score(y_test, y_pred) print(f'Accuracy: {accuracy}') # 从测试集中随机选择5个样本 sample_indices = random.sample(range(len(X_test)), 5) for idx in sample_indices:     sample_image = X_test[idx].reshape(100, 100, 3)     true_label = class_labels[y_test[idx]]     predicted_label = class_labels[y_pred[idx]]     plt.imshow(sample_image)     plt.title(f'True Label: {true_label}, Predicted Label: {predicted_label}')     plt.show()

3：实验指导中的参考代码（修改后）

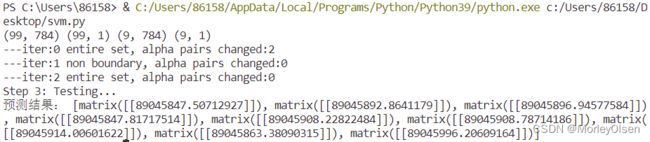
from numpy import * import numpy as np import random # calulate kernel value def calcKernelValue(matrix_x, sample_x, kernelOption):     kernelType = kernelOption[0]     numSamples = matrix_x.shape[0]     kernelValue = mat(zeros((numSamples, 1)))     if kernelType == 'linear':         kernelValue = matrix_x * sample_x.T     elif kernelType == 'rbf':         sigma = kernelOption[1]         if sigma == 0:             sigma = 1.0         for i in range(numSamples):             diff = matrix_x[i, :] - sample_x             kernelValue[i] = exp(diff * diff.T / (-2.0 * sigma ** 2))     else:         raise NameError('Not support kernel type! You can use linear or rbf!')     return kernelValue # calculate kernel matrix given train set and kernel type def calcKernelMatrix(train_x, kernelOption):     numSamples = train_x.shape[0]     kernelMatrix = mat(zeros((numSamples, numSamples)))     for i in range(numSamples):         kernelMatrix[:, i] = calcKernelValue(train_x, train_x[i, :], kernelOption)     return kernelMatrix # define a struct just for storing variables and data class SVMStruct:     def __init__(self, dataSet, labels, C, toler, kernelOption):         self.train_x = dataSet         self.train_y = labels         self.C = C         self.toler = toler         self.numSamples = dataSet.shape[0]         self.alphas = mat(zeros((self.numSamples, 1)))         self.b = 0         self.errorCache = mat(zeros((self.numSamples, 2)))         self.kernelOpt = kernelOption         self.kernelMat = calcKernelMatrix(self.train_x, self.kernelOpt) # calculate the error for alpha k def calcError(svm, alpha_k):     output_k = float(multiply(svm.alphas, svm.train_y).T * svm.kernelMat[:, alpha_k] + svm.b)     error_k = output_k - float(svm.train_y[alpha_k])     return error_k # update the error cache for alpha k after optimize alpha k def updateError(svm, alpha_k):     error = calcError(svm, alpha_k)     svm.errorCache[alpha_k] = [1, error] # select alpha j which has the biggest step def selectAlpha_j(svm, alpha_i, error_i):     svm.errorCache[alpha_i] = [1, error_i]     candidateAlphaList = nonzero(svm.errorCache[:, 0].A)[0]     maxStep = 0     alpha_j = 0     error_j = 0     if len(candidateAlphaList) > 1:         for alpha_k in candidateAlphaList:             if alpha_k == alpha_i:                 continue             error_k = calcError(svm, alpha_k)             if abs(error_k - error_i) > maxStep:                 maxStep = abs(error_k - error_i)                 alpha_j = alpha_k                 error_j = error_k     else:         alpha_j = alpha_i         while alpha_j == alpha_i:             alpha_j = int(random.uniform(0, svm.numSamples))         error_j = calcError(svm, alpha_j)     return alpha_j, error_j # the inner loop for optimizing alpha i and alpha j def innerLoop(svm, alpha_i):     error_i = calcError(svm, alpha_i)     if (svm.train_y[alpha_i] * error_i < -svm.toler) and (svm.alphas[alpha_i] < svm.C) or (             svm.train_y[alpha_i] * error_i > svm.toler) and (svm.alphas[alpha_i] > 0):         alpha_j, error_j = selectAlpha_j(svm, alpha_i, error_i)         alpha_i_old = svm.alphas[alpha_i].copy()         alpha_j_old = svm.alphas[alpha_j].copy()         if svm.train_y[alpha_i] != svm.train_y[alpha_j]:             L = max(0, svm.alphas[alpha_j] - svm.alphas[alpha_i])             H = min(svm.C, svm.C + svm.alphas[alpha_j] - svm.alphas[alpha_i])         else:             L = max(0, svm.alphas[alpha_j] + svm.alphas[alpha_i] - svm.C)             H = min(svm.C, svm.alphas[alpha_j] + svm.alphas[alpha_i])         if L == H:             return 0         eta = 2.0 * svm.kernelMat[alpha_i, alpha_j] - svm.kernelMat[alpha_i, alpha_i] - svm.kernelMat[alpha_j, alpha_j]         if eta >= 0:             return 0         svm.alphas[alpha_j] -= svm.train_y[alpha_j] * (error_i - error_j) / eta         if svm.alphas[alpha_j] > H:             svm.alphas[alpha_j] = H         if svm.alphas[alpha_j] < L:             svm.alphas[alpha_j] = L         if abs(alpha_j_old - svm.alphas[alpha_j]) < 0.00001:             updateError(svm, alpha_j)             return 0         svm.alphas[alpha_i] += svm.train_y[alpha_i] * svm.train_y[alpha_j] * (alpha_j_old - svm.alphas[alpha_j])         b1 = svm.b - error_i - svm.train_y[alpha_i] * (svm.alphas[alpha_i] - alpha_i_old) * svm.kernelMat[             alpha_i, alpha_i] * svm.train_y[alpha_j] * (svm.alphas[alpha_j] - alpha_j_old) * svm.kernelMat[             alpha_i, alpha_j]         b2 = svm.b - error_j - svm.train_y[alpha_i] * (svm.alphas[alpha_i] - alpha_i_old) * svm.kernelMat[             alpha_i, alpha_j] - svm.train_y[alpha_j] * (svm.alphas[alpha_j] - alpha_j_old) * svm.kernelMat[             alpha_j, alpha_j]         if (0 < svm.alphas[alpha_i]) and (svm.alphas[alpha_i] < svm.C):             svm.b = b1         elif (0 < svm.alphas[alpha_j]) and (svm.alphas[alpha_j] < svm.C):             svm.b = b2         else:             svm.b = (b1 + b2) / 2.0         updateError(svm, alpha_j)         updateError(svm, alpha_i)         return 1     else:         return 0 # the main training procedure def trainSVM(train_x, train_y, C, toler, maxIter, kernelOption=('rbf', 1.0)):     svm = SVMStruct(mat(train_x), mat(train_y), C, toler, kernelOption)     entireSet = True     alphaPairsChanged = 0     iterCount = 0     while (iterCount < maxIter) and ((alphaPairsChanged > 0) or entireSet):         alphaPairsChanged = 0         if entireSet:             for i in range(svm.numSamples):                 alphaPairsChanged += innerLoop(svm, i)             print('---iter:%d entire set, alpha pairs changed:%d' % (iterCount, alphaPairsChanged))             iterCount += 1         else:             nonBoundAlphasList = nonzero((svm.alphas.A > 0) * (svm.alphas.A < svm.C))[0]             for i in nonBoundAlphasList:                 alphaPairsChanged += innerLoop(svm, i)             print('---iter:%d non boundary, alpha pairs changed:%d' % (iterCount, alphaPairsChanged))             iterCount += 1         if entireSet:             entireSet = False         elif alphaPairsChanged == 0:             entireSet = True     return svm # testing your trained svm model given test set def testSVM(svm, test_x):     test_x = mat(test_x)     numTestSamples = test_x.shape[0]     supportVectorsIndex = nonzero(svm.alphas.A > 0)[0]     supportVectors = svm.train_x[supportVectorsIndex]     supportVectorLabels = svm.train_y[supportVectorsIndex]     supportVectorAlphas = svm.alphas[supportVectorsIndex]     re_predict = []     for i in range(numTestSamples):         kernelValue = calcKernelValue(supportVectors, test_x[i, :], svm.kernelOpt)         predict = kernelValue.T * multiply(supportVectorLabels, supportVectorAlphas) + svm.b         re_predict.append(predict)     return re_predict # Standardize the data def Standar(data):     mean = np.mean(data, axis=1).reshape(-1, 1)     std = np.std(data, axis=1).reshape(-1, 1)     another_trans_data = data - mean     return another_trans_data / std if __name__ == '__main__':     C, toler, maxIter = 0.6, 0.001, 40     train_data = np.load(r'C:\Users\86158\Desktop\mnist_train_100.npy')     test_data = np.load(r'C:\Users\86158\Desktop\mnist_test_10.npy')     train_x, y_train, test_x, y_test = train_data[:, 1:], train_data[:, 0].reshape(-1, 1), test_data[:, 1:], test_data[:,0].reshape(-1, 1)     X_large_train = Standar(train_x)     X_large_test = Standar(test_x)     print(train_x.shape, y_train.shape, test_x.shape, y_test.shape)     svmClassifier = trainSVM(X_large_train, y_train, C, toler, maxIter, kernelOption=('linear', 0))     print("Step 3: Testing...")     predict = testSVM(svmClassifier, X_large_test)     print("预测结果：", predict)

4：csv文件转换为npy文件的代码

import pandas as pd import numpy as np # 从CSV文件加载数据 csv_file = r'C:\Users\86158\Desktop\mnist_test_10.csv' data = pd.read_csv(csv_file) # 将数据转换为NumPy数组 data_array = data.to_numpy() # 保存为NPY文件 npy_file = r'C:\Users\86158\Desktop\mnist_test_10.npy' np.save(npy_file, data_array) print(f"CSV文件 '{csv_file}' 已成功转换为 NPY文件 '{npy_file}'")