union-find算法

        并查集，即能进行合并(union)与查询(find)的一种数据结构。用来快速判断两个元素的连通性。

union-find算法学习笔记

并查集(union-find)算法详解

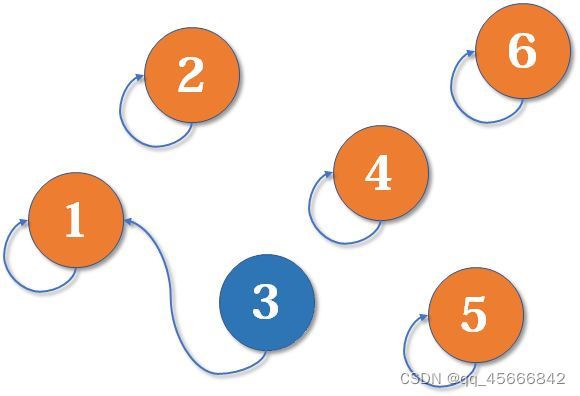
例如：A-F, B-C, Z-H, C-F...一对字母表示两地之间的航班，判断是否可以坐飞机从某地到达另一个地方；也可以表示电子通路，判断两个节点是否通电；或者判断两个人之间是否有某种联系......在某些问题中，可能要处理数十亿对数据判断连通性。 这一问题成为动态连通性

随着数据的输入，整个图的动态连通性也会不断地发生变化。

          触点：上图中的一个数字代表一个触点

          分量：一个连通的整体代表一个分量，上图最终有两个分量

并查集的实现方式

 对问题建模：

在对问题进行建模的时候，我们应该尽量想清楚需要解决的问题是什么。因为模型中选择的数据结构和算法显然会根据问题的不同而不同，就动态连通性这个场景而言，我们需要解决的问题可能是：

        给出两个节点，判断它们是否连通，如果连通，不需要给出具体的路径
        给出两个节点，判断它们是否连通，如果连通，需要给出具体的路径

就上面两种问题而言，虽然只有是否能够给出具体路径的区别，但是这个区别导致了选择算法的不同，本文主要介绍的是第一种情况，即不需要给出具体路径的Union-Find算法，而第二种情况可以使用基于DFS的算法。

原文连接：https://blog.csdn.net/dm_vincent/article/details/7655764 

         为了说明问题，设计简洁的API封装所需的基本操作，API如下

初始化(UF)、连接两个触点(union) 、找到指定点所在的分量标识符(find)、判断两个触电是否连通(connected)、返回分量个数(count)。

一、quick-find算法

        首先是最简单的方法，假设有N个触点，我们创建一个长度为N的整数型数组id[ ]，在同一个分量中的触点id[ ]必须相同。所以connected（int p, int q）只需要判断返回 id[p] == id[q]的布尔值即可。find(int p)返回的整数即是id[p]。union(int p,int q)方法即先判断p、q是否处于同一个分量中，若在同一个分量中则不做任何操作，反之需要将p和q所在分量的所有触点对应的元素id[ ] 变为同一个值。

        quick-find，顾名思义，在用find方法查找触点所在的分量标识符时，相比于其他方法所用时间较短，然而union方法则用时较长。

public class QuickFindUF
{
    priavte int[] id;
    private int count;

    public QuickFindUF(int N)
    { 
        count = N;
        id = new int[N];
        for(int i = 0;i

      find()方法是很快的，只需要访问id[ ] 数组一次，但是该算法却无法处理大型问题，因为每一对新连接的输入，union()方法都要遍历一次id[ ] 数组。 

        当union() 方法连接两个分量时，首先获得两个分量的id[p]和id[q]，访问数组2次。然后遍历数组访问数组N次，可能该变数组元素1 ~ N-1个值。所以当union方法连接两个分量时访问数组的次数为(N+3)~(2N+1)次之间                                                                                                           （2+N+1)~(2+N+N-1)

N个触点最后得到一个连通分量最少要调用N-1次union方法，因此访问id[]数组的次数最少为(N+3)*(N-1), 也就是说quick-find算法的动态连通性问题是平方级别的，在处理大型问题上是不可行的。

二、quick-union算法

        相比于quick-find算法，其connected()、count() 方法不变，仍然使用一个大小为N的整数型数组id[ ]。数组初始化与quick-find算法一样，id[0] = 0、id[1] = 1.......，每个触点代表一个分量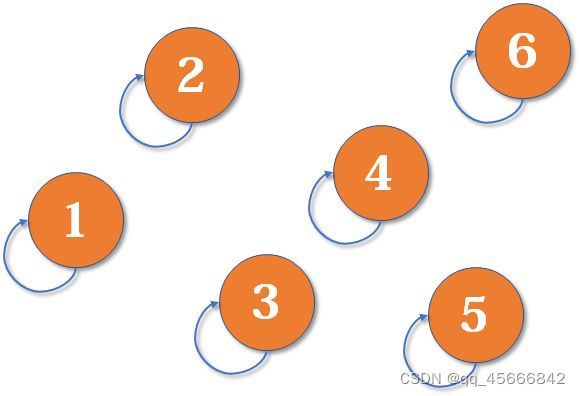

        当添加一组连接如：3-1时，这时3、1分别属于两个不同的分量，两个分量的代表触点都是它本身(因为触点连接指向自己)，令id[3] = 1,使前者3指向后者1，这时3和1已经连接成一个分量，该分量由1来代表。哪个触点的连接指向自己，那么他就是所在分量的代表触点。这是id[ ] 数组的变化为：

 再添加连接2-3时，3所在分量的代表触点是1，所以令2指向1，即id[2] = 1。

假设4、5、6也进行了类似的连接(添加5-4、6-5)

 再添加连接6-3，6、3分别在不同的分量里面，而且两个分量的代表触点分别为4、1。使id[4] = 1;

通过上述操作便将所有的触点都连接在了同一个分量里面。综上所述，连接两个分量时，使其中一个分量的代表触点连接到另一个分量的代表触点，这样就完成了两个分量的连接。  接下来看具体的代码实现

public class QuickUnionUF
{
    priavte int[] id;
    private int count;

    public QuickUnionUF(int N)
    { 
        count = N;
        id = new int[N];
        for(int i = 0;i

 该算法相比于quick-find算法有很大提升，但是存在最坏情况，运算时间是平方级的。

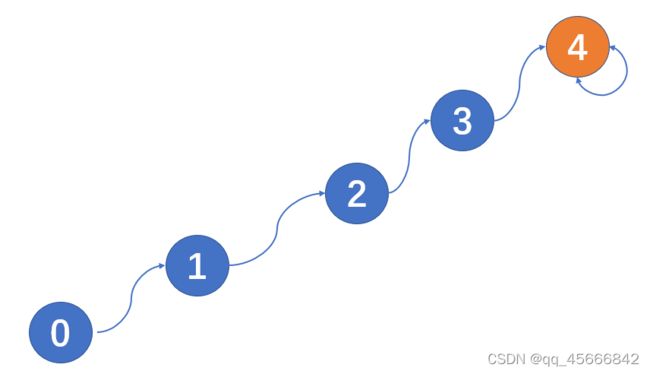
如：逐步添加连接0-1、0-2、0-3、0-4...

 

 

 

 

以上图均来自于算法笔记-并查集

 发生以上情况的原因是什么，是因为这个算法不管两个分量谁大谁小(两棵树谁大谁小)，总是把前者的分量添加在后者分量的后面。这样会导致树的高度变高，find方法查找访问数组次数变多。

三、加权的quick-union算法

        添加一个参数，能够记录分量的数的大小（），连接两个分量时将较小的树添加到较大的树上，这样就能够避免最坏情况的发生。注意：这里只是按照树的大小，而不是树的高度，有可能会出现高度较高的树连接到高度较矮的树上，这里暂时不讨论。

 添加一个整数型数组sz[ ]，大小为触点数N, 初始化为1，表示每个触点代表一个分量里面的触点个数为1。合并两个分量之后重新计算分量的大小。具体实现如下

public class QuickUnionWeightedUF
{
    priavte int[] id;
    private int[] sz;
    private int count;

    public QuickUnionWeightedUF(int N)
    { 
        count = N;
        id = new int[N];
        for(int i = 0;i

对于N个触点，加权quick-union的算法构造森林中的任意节点的深度最多为logN; 

在最坏情况下find()、connected()、union()的成本的增长数量级为logN。

 四、最优算法--路径压缩方法

        理想情况下，我们希望每个节点都直接连接到它的根结点上，但是又要避免大批修改连接，因为那样可能会得不偿失。只需要对加权quick-union算法略加改进，添加一个循环，在检查节点的同时直接将路径上的节点链接到根节点上。

以上图为例，在寻找7的根节点过程，即find(7)过程中，将路径上的节点都链接到根节点上。首先一个循环找到指定节点的根节点，然后添加一个循环便路径上的节点，将节点链接到根节点上。

public int find(int p)
{
    int root = p;
    while(root!=id[root])
        root = id[root];
    while(id[p] != root)
    {
        int newP = p;
        id[newP] = root;
        p = id[p];
    }
}

 其余均与加权quick-union算法一致。