力扣算法：24、两两交换链表中的节点 19、删除链表的倒数n个节点 07、链表相交 142、环形链表||

学习内容

力扣算法：

24、两两交换链表中的节点

19、删除链表的倒数n个节点

07、链表相交

142、环形链表||

具体内容

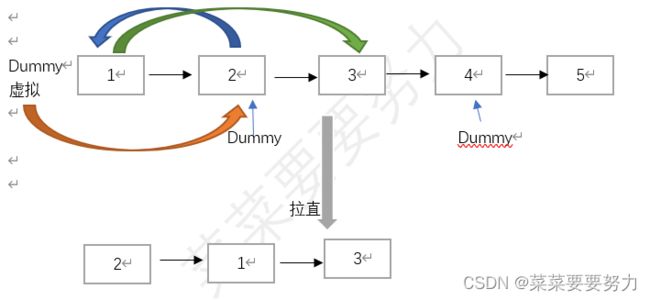
24、两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

输入：head = [1,2,3,4] 输出：[2,1,4,3]

示例 2：

输入：head = [] 输出：[]

示例 3：

输入：head = [1] 输出：[1]

题目地址

解题

class Solution {
    public ListNode swapPairs(ListNode head) {
    	ListNode listnode = new ListNode(-1,head);
    	ListNode pre = listnode;
    	//判断链表长度为单数还是偶数
    	while(pre.next != null && pre.next.next != null){
    		ListNode cur = pre.next;
    		ListNode cur1 = pre.next.next.next;
    		pre.next = pre.next.next;
    		pre.next.next = cur;
    		cur.next = cur1;
    		cur = cur.next.next;
    	}
    	return listnode.next;
    }
}

代码中需要注意的地方

1、 while循环体的判断语句为何这样写

pre.next != null 判断链表个数为偶数， pre.next.next != null判断链表个数为奇数

2、在翻转指针时要多画图理解

cur虚拟头节点一定是指向要交换的两个节点的前一个节点

3、为什么while循环体是用&& 而不是||

结合图像判断，pre.next != null表示链表长度是单数，pre.next.next != null代表链表长度是双数，可结合上图来看

19、删除链表的倒数n个节点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

输入：head = [1,2,3,4,5], n = 2 输出：[1,2,3,5]

示例 2：

输入：head = [1], n = 1 输出：[]

示例 3：

输入：head = [1,2], n = 1 输出：[1]

题目地址

解题

快慢指针

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
    	//设立虚拟头节点
    	ListNode listnode = new ListNode(-1,head);
    	//快指针
    	ListNode fast = listnode;
    	//慢指针
    	ListNode slow = listnode;
    	//n取值要n+1 即n=0时依然循环 才能使slow到达要删除节点的前一个位置
    	while(n-- >= 0{
    		fast = fast.next;
    	}
    	while(fast != null){
    		fast = fast.next;
    		slow = slow.next;
			}
			slow.next = slow.next.next;
			return listnode.next;
		}
}

代码中需要注意的地方

1、为什么求倒数第n个节点时，快指针走n+1步之后，slow紧跟后面直到快指针等于null，慢指针指向的便是我们所求的值？

双指针的经典应用，如果要删除倒数第n个节点，让fast移动n步，然后让fast和slow同时移动，直到fast指向链表末尾。删掉slow所指向的节点就可以了。

07、链表相交

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交：

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

示例 1：

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA
= 2, skipB = 3 输出：Intersected at ‘8’ 解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。 从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。 在 A 中，相交节点前有 2
个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3,
skipB = 1 输出：Intersected at ‘2’ 解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。 在 A 中，相交节点前有 3 个节点；在 B
中，相交节点前有 1 个节点。

示例 3：

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB
= 2 输出：null 解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。 由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。 这两个链表不相交，因此返回 null 。

解题

题目地址

public class Solution {
    //此题关键是要两个链表都从同一个位置开始遍历 因此一定要从短的链表开始往后遍历啊
    //因此要求其长度
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    	ListNode curA = headA;
    	ListNode curB = headB;
		int lenA = 0;
		int lenB = 0;
		//求A链表长度
		while(curA != null){
			lenA++;
			curA = curA.next;
		}
		//求B链表长度
		while(curB != null){
			lenB++;
			curB = curB.next;
		}
		//curA和curB初始化
		curA = headA;
    	curB = headB;
		//统一让lenA最长
		if(lenB > lenA){
			int temp = lenA;
			lenA = lenB;
			lenB =  temp;

			ListNode list = curA;
			curA = curB;
			curB = list;
		}
		//求长度差
		int pre = lenA - lenB;
		while(pre-- > 0){
			curA = curA.next;
		}
		while(curA != null){
			if(curA == curB){
				return curA;
			}
			curA = curA.next;
			curB = curB.next;
		}
		return null;
   }
}

解答代码存在的疑问

1、解题步骤

求两条长度不同链表相交的相同元素，由于长度不同，因此为了统一规则，可以先找出各自的链表长度，求长度差n，而较长链表在n个元素之前都不会与短链表相交，因此先让长链表遍历到n的位置，这样长短链表属于同一起点，便可一直往下走

142、环形链表||

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1 输出：返回索引为 1 的链表节点 解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0 输出：返回索引为 0 的链表节点 解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1 输出：返回 null 解释：链表中没有环。

解题

题目地址

public class Solution {
    public ListNode detectCycle(ListNode head) {
    	ListNode fast = head;
    	ListNode slow = head;
    	//快指针走两步 慢指针走一步
    	while(fast != null && fast.next != null){
    		fast = fast.next.next;
    		slow = slow.next;
    		//再从head出发 获取相遇的位置
             while (index1 != index2) {
                 index1 = index1.next;
                 index2 = index2.next;
             }
             return index2; // 返回环的入口
    	}
    }
}

解答代码存在的疑问

1、当求出了快慢指针的相遇位置时，为什么还要再用while循环求？

求出了快慢指针的相遇位置，只知道了fast在哪，还要求入口

复习

24、两两交换链表中的节点

存在错误，逻辑不清楚，要记住，要改变链表节点的方向，就一定要获得前一个结点这样才可以改变指向

class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode pre = head;
        ListNode cur = null;
        while(pre != null){
            cur = pre.next;
            pre.next = pre.next.next;
            cur.next = pre;
            pre = cur;
            cur = pre.next;
        }
        return head;
    }
}

矫正后

从后往前

class Solution {
  public ListNode swapPairs(ListNode head) {

    ListNode dummyNode = new ListNode(0);
    dummyNode.next = head;
    ListNode prev = dummyNode;

    while (prev.next != null && prev.next.next != null) {
      ListNode temp = head.next.next; // 缓存 next
      prev.next = head.next;          // 将 prev 的 next 改为 head 的 next
      head.next.next = head;          // 将 head.next(prev.next) 的next，指向 head
      head.next = temp;               // 将head 的 next 接上缓存的temp
      prev = head;                    // 步进1位
      head = head.next;               // 步进1位
    }
    return dummyNode.next;
  }
}

19、删除链表的倒数n个节点

逻辑存在错误

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
       ListNode fastIndex = head;
    ListNode slowIndex = head;

    
    for (int i = 0; i < n  ; i++){
        fastIndex = fastIndex.next;
    }

    while (fastIndex != null){
        fastIndex = fastIndex.next;
        slowIndex = slowIndex.next;
    }
   
    slowIndex.next = fastIndex;
    return head;
    }
}

矫正后

public ListNode removeNthFromEnd(ListNode head, int n){
    ListNode dummyNode = new ListNode(0);
    dummyNode.next = head;
    ListNode fastIndex = dummyNode;
    ListNode slowIndex = dummyNode;

    //只要快慢指针相差 n 个结点即可
    for (int i = 0; i < n  ; i++){
        fastIndex = fastIndex.next;
    }

    while (fastIndex.next != null){
        fastIndex = fastIndex.next;
        slowIndex = slowIndex.next;
    }

    //此时 slowIndex 的位置就是待删除元素的前一个位置。
    //具体情况可自己画一个链表长度为 3 的图来模拟代码来理解
    slowIndex.next = slowIndex.next.next;
    return dummyNode.next;
}

07、链表相交

完全已忘记

ublic class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode curA = headA;
        ListNode curB = headB;
        int lenA = 0, lenB = 0;
        while (curA != null) { // 求链表A的长度
            lenA++;
            curA = curA.next;
        }
        while (curB != null) { // 求链表B的长度
            lenB++;
            curB = curB.next;
        }
        curA = headA;
        curB = headB;
        // 让curA为最长链表的头，lenA为其长度
        if (lenB > lenA) {
            //1. swap (lenA, lenB);
            int tmpLen = lenA;
            lenA = lenB;
            lenB = tmpLen;
            //2. swap (curA, curB);
            ListNode tmpNode = curA;
            curA = curB;
            curB = tmpNode;
        }
        // 求长度差
        int gap = lenA - lenB;
        // 让curA和curB在同一起点上（末尾位置对齐）
        while (gap-- > 0) {
            curA = curA.next;
        }
        // 遍历curA 和 curB，遇到相同则直接返回
        while (curA != null) {
            if (curA == curB) {
                return curA;
            }
            curA = curA.next;
            curB = curB.next;
        }
        return null;
    }
}

142、环形链表||

完全已忘记

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode pre = head;
        ListNode cur = head;
        while(pre != null && pre.next != null){
            cur = cur.next;
            pre = pre.next.next;
            if(cur == pre){
                ListNode index1 = pre;
                ListNode index2 = head;
                // 两个指针，从头结点和相遇结点，各走一步，直到相遇，相遇点即为环入口
                while (index1 != index2) {
                    index1 = index1.next;
                    index2 = index2.next;
                }
                return index1;
            }
        }
        return null;
    }
}