1.12 力扣中等图论

797. 所有可能的路径 - 力扣（LeetCode）

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

 graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

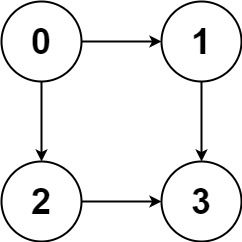
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

思路：

使用dfs深度优先算法，从起点0开始遍历当前可去节点有哪些，直到走到终点target

递归函数参数

当前节点cur，终点target，图信息graph，当前path经过节点记录，当前路径curPath，最后结果ret

    void dfs(int cur,int target,vector>& graph,unordered_set& setPath,vector& curPath,vector>& ret)

递归终止条件：cur==target

递归内容：

循环进入当前节点可去的节点，寻找可行方案

        for(int e:graph[cur])
        {
            if(setPath.count(e)) continue;

            setPath.insert(e);
            curPath.push_back(e);
            dfs(e,target,graph,setPath,curPath,ret);
            setPath.erase(e);
            curPath.pop_back();
        }

class Solution {
public:
    void dfs(int cur,int target,vector>& graph,unordered_set& setPath,vector& curPath,vector>& ret)
    {
        if(cur==target)
        {
            ret.push_back(curPath);
            return;
        }
        for(int e:graph[cur])
        {
            if(setPath.count(e)) continue;

            setPath.insert(e);
            curPath.push_back(e);
            dfs(e,target,graph,setPath,curPath,ret);
            setPath.erase(e);
            curPath.pop_back();
        }
        return;
    }
    vector> allPathsSourceTarget(vector>& graph) {
        int target=graph.size()-1;//终点
        unordered_set setPath;
        vector curPath;
        //加入起点
        curPath.push_back(0);
        setPath.insert(0);

        vector> ret;
        dfs(0,target,graph,setPath,curPath,ret);
        return ret;
    }
};