蓝桥杯精选赛题算法系列——翻硬币——贪心法

已收录此专栏。
今天我们来学一学贪心算法。

贪心（Greedy）可以说是最容易理解的算法思想：把整个问题分解成多个步骤，在每个步骤，都选取当前步骤的最优方案，直到所有步骤结束；在每一步，都不考虑对后续步骤的影响，在后续步骤中也不再回头改变前面的选择。简单地说，其思想就是“走一步看一步”、“目光短浅”。

那这贪心法有啥用呢？
贪心法有广泛的应用。例如图论中的最小生成树算法、单源最短路径算法Dijkstra，是贪心思想的典型应用。下面我们先用硬币问题的例子，引导出贪心法的应用规则吧。

题目描述：某人带着3种面值的硬币去购物，有1元、2元、5元的，硬币数量不限；他需要支付M元，问怎么支付，才能使硬币数量最少？

根据生活常识，第一步应该先拿出面值最大的 5​ 元硬币，第二步拿出面值第二大的 2​ 元硬币，最后才拿出面值最小的 1​ 元硬币。在这个解决方案中，硬币数量总数是最少的。
我们先来用暴力法来编写一下这个程序：

m  = int(input())
if m>=5:
    cnt = m//5
    m = m-cnt*5
    if m == 0:
        print(cnt)
if m>=2:
    cnttwo = m//2
    cnt += m//2
    m = m-cnttwo*2
    if m == 0:
        print(cnt)
if m>=1:
    cntone = m//1
    cnt += m//1
    m = m-cntone*1
    if m == 0:
        print(cnt)

代码简单，而且计算量极小！贪心法可以说是计算复杂度最低的算法了，而暴力法是计算复杂度最差的。
在上面的例子中，虽然每一步选硬币的操作，并没有从整体最优来考虑，而是只在当前步骤选取了局部最优，但是结果是全局最优的。

局部最优不会导致全局最优。
这个我们一定要注意。

就比如这个最少硬币问题，用贪心法一定能得到最优解吗？答案是：不能。
如果我稍微改换一下参数，就不一定能得到最优解，甚至在有解的情况下也无法算出答案。
我们举个例子：

1.不能得到最优解的情形。例如，硬币面值比较奇怪，是 1、2、4、5、6元 。现在来支付 9 元，如果用贪心法，答案是 6 + 2+ 1，需要 3 个硬币，而最优的 5 + 4 只需要 2 个硬币。
2.算不出答案的情形。例如，如果有面值 1 元的硬币，能保证用贪心能得到一个解，如果没有 1 元硬币，常常得不到解。例如只有面值 2、3、5 元的硬币，支付 9元，用贪心法无法得到解，但解是存在的：9 = 5 + 2 + 2。

所以，在最少硬币问题中，是否能使用贪心法，跟硬币的面值有关。如果是 1​​​​​​​、2​​​​​​​、5​​​​​​​ 这样的面值，贪心是有效的，而对于 1​​​​​​​、2​​​​​​、4​​​​​、5​​​​、6​​​ 或者 2​​、3​、5 这样的面值，贪心是无效的。
那对于任意面值的硬币问题，有没有确定的解法？那肯定是有的，那就是用动态规划，这个算法我之后也会在这个专栏更新。不过这里有必要说说贪心和动态规划的关系：一个题目如果用贪心无法求最优解，往往能用动态规划求最优解。
好，回到贪心正题，虽然贪心法不一定能得到最优解，但是它思路简单、编程容易。因此，如果一个问题确定用贪心法能得到最优解，那么应该使用它。
那如何判断一个题目能用贪心？

贪心法求解的问题，需要满足以下特征：
1.最优子结构性质。当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质，也称此问题满足最优性原理。也就是说，从局部最优能扩展到全局最优。
2.贪心选择性质。问题的整体最优解可以通过一系列局部最优的选择来得到。

贪心算法没有固定的算法框架，关键是如何选择贪心策略。
所谓贪心策略，必须具备无后效性，即某个状态以后的过程不会影响以前的状态，只与当前状态有关。另外，把贪心法用在“虽然不是最好，但是还不错，我表示满意！”的某些难解问题上，例如旅行商问题，是很难得到最优解的。但是用贪心法常常能得到不错的近似解。如果不一定非要求得最优解，那么贪心的结果，也是很不错的方案。
这么听起来是不是觉得贪心算法非常不靠谱，因为局部最优的组合，不一定是全局最优的。不过是否存在一些规则，使得局部最优能达到全局最优？也就是说，有没有一个一般性的数学理论，可以证明一个问题能用贪心法？
有的。有一个叫做“拟阵”的理论，虽然它不能覆盖所有贪心法适用的情况，但是在很多情况下能确定贪心法能产生最优解。有兴趣的话可以去了解了解。
接下来，我会用几个常见问题来帮助你建立贪心法的思维，后面再用比赛题巩固哦。

活动安排问题（又称为区间调度问题）

题目描述：有很多电视节目，给出它们的起止时间。有的节目时间冲突。问能完整看完的电视节目最多有多少？

输入：输入数据包含多个测试实例，每个测试实例的第一行只有一个整数 n(n<=100)，表示节目总数，然后是 n 行数据，每行包括两个数据 s,e(1≤i≤n)，分别表示第 i 个节目的开始和结束时间，为了简化问题，每个时间都用一个正整数表示。n=0 表示输入结束，不做处理。
输出：对于每个测试实例，输出能完整看到的电视节目的个数，每个测试实例的输出占一行。

解题的关键在于选择什么贪心策略，才能安排尽量多的活动。你能想到哪些贪心策略呢？
活动有开始时间和结束时间⋯ 我想到了三种贪心策略：
1.最早开始时间。
2.最早结束时间。
3.用时最少。

那我们来分析一下这三种策略吧：
首先第 1 种策略是错误的，因为如果一个活动迟迟不终止，后面的活动就无法开始。
第 2 种策略是合理的，尽快终止一个活动，可以容纳更多的后续活动。
而第 3​​ 种策略也显然错误的。

那我们就对最早结束时间进行贪心。算法步骤是：
1.把 n 个活动按结束时间排序。
2.选择第一个结束的活动，并删除（或跳过）与它时间相冲突的活动。
3.重复步骤 2​，直到活动为空。每次选择剩下的活动中最早结束的那个活动，并删除与它时间冲突的活动。
下面的图是例子，最优活动是 1​、3​、5，活动 2、4 与其它节目有冲突。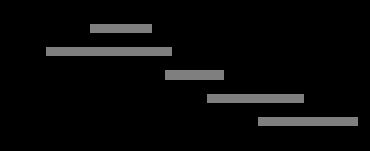
图1 活动安排
我们来分析一下该策略的特征：
1.它符合最优子结构性质。选中的第 1 个活动，它一定在某个最优解中；同理，选中的第 2 个活动、第 3 个活动……也同样在这个最优解中。
2.它符合贪心选择性质。算法的每一步都使用了相同的贪心策略。
下面是代码：

s = [[] for i in range(100)]
while 1:
    n = int(input())
    if n  == 0 :
        break
    for i in range(0,n):
       a,b = map(int,input().split())
       s[i].append(a)
       s[i].append(b)
    while [] in s:
        s.remove([])
    s = sorted(s,key = lambda s:s[1])
    last = -1
    count = 0
    for i in range(0,n):
            if s[i][0] >= last:
                count += 1
                last = s[i][1]
    print(count)

下面再来看一下

区间覆盖问题

题目描述：给定一个长度为 n 的区间，再给出 m 条线段的左端点（起点）和右端点（终点）。问最少用多少条线段可以将整个区间完全覆盖。

贪心策略：那就要尽量找出更长的线段
解题步骤为：
1.把每个线段按照左端点递增排序。
2.设已经覆盖的区间是 [L, R] ，在剩下的线段中，找所有左端点小于等于 R，且右端点最大的线段，把这个线段加入到已覆盖区间里，并更新已覆盖区间的 [L, R] 值。
3.重复步骤 2，直到区间全部覆盖。
图2 区间覆盖
图 2 中，所有线段已按左端点进行排序。于是首先选中线段 1，然后在 2 和 3 中，选中更长的 3 。而 4 和 5 由于不合要求，被跳过。最后的最优解是 1、3。

再来分析一下

最优装载问题（也被称为普通背包问题）

题目描述：有 n 种药水，体积都是 V ，浓度不同。把它们混合起来，得到浓度不大于 w%的药水。问怎么混合，才能得到最大体积的药水？注意一种药水要么全用，要么都不用，不能只取一部分。

题目要求配置浓度不大于 w% 的药水。
贪心策略：尽量找浓度小的药水。
于是先对药水按浓度从小到大排序，药水的浓度不大于 w% 就加入，如果药水的浓度大于 w%，计算混合后总浓度，不大于 w​% 就加入，否则结束判断。

多机调度问题

题目描述：设有 n 个独立的作业，由 m 台相同的机器进行加工。作业 i 的处理时间为 ti ，每个作业可在任何一台机器上加工处理，但不能间断、拆分。要求给出一种作业调度方案，在尽可能短的时间内，由 m 台机器加工处理完成这 n​​个作业。

求解多机调度问题的贪心策略是：最长处理时间的作业优先，即把处理时间最长的作业分配给最先空闲的机器。让处理时间长的作业得到优先处理，从而在整体上获得尽可能短的处理时间。

1.如果n≤m，需要的时间就是 n 个作业当中最长处理时间 t。

2.如果 n>m，首先将 n 个作业按处理时间从大到小排序，然后按顺序把作业分配给空闲的机器。

题目描述

小明正在玩一个"翻硬币"的游戏。

桌上放着排成一排的若干硬币。我们用 * 表示正面，用 o 表示反面（是小写字母，不是零）。

比如，可能情形是：oo*oooo;

如果同时翻转左边的两个硬币，则变为：oooo***oooo。

现在小明的问题是：如果已知了初始状态和要达到的目标状态，每次只能同时翻转相邻的两个硬币,那么对特定的局面，最少要翻动多少次呢？

我们约定：把翻动相邻的两个硬币叫做一步操作。

输入描述

两行等长的字符串，分别表示初始状态和要达到的目标状态。

每行的长度<1000。

输出描述

一个整数，表示最小操作步数。

输入输出样例

示例

输入

**********
o****o****

输出

5

思路：首先确定：一个字符串 S1如果可以通过翻转相邻两个的字符变成另一个字符串 S2，则 S1 、S2必定有偶数个字符不同。然后思考贪心的过程，是不是从局部最优到全局最优。我们从左边开始找第一个不同的那个字符（称它为 Z），Z 左边的字符都相同，不用再翻动。Z 右边肯定有偶数个不同的字符。而 Z 是必定要翻动的，不能不翻。它翻了之后，就不用再翻动。所以从左到右的翻动过程，每次翻动都是必须的，也就是说这个翻动 Z 的局部最优操作，也是全局最优操作。所以贪心是正确的。

s1 = list(input())
s2 = list(input())
ans = 0
for i in range(len(s1) - 1):
    if s1[i] != s2[i]:
        if s1[i + 1] == 'o': s1[i + 1] = '*'
        else:                s1[i + 1] = 'o'
#Python也有类似的三目运算，把上面2行换成：
#       s1[i + 1] = '*' if s1[i + 1] == 'o' else 'o'
        ans += 1
print(ans)