栈练习之Example007-利用栈判定单链表是否中心对称
Example007
题目
设单链表的表头指针为 L,结点结构由 data 和 next 两个域构成,其中 data 域为字符型。试设计算法判定该链表的全部 n 个字符是否中心对称。例如 xyx、xyyx 都是中心对称。
分析
算法思想:
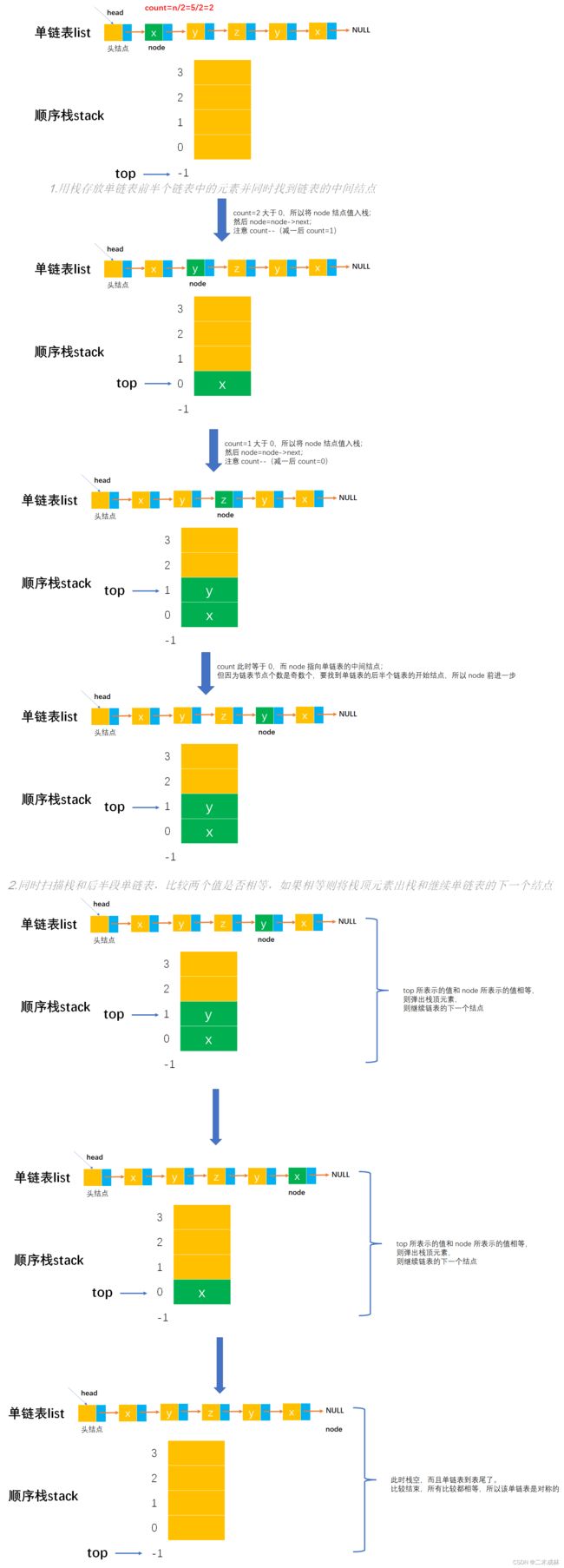
使用栈来判断链表中的数据是否中心对称。让链表的前一半元素依次进栈。在处理链表的后一半元素时,当访问到链表的第一个元素后,就从栈中弹出一个元素,两个元素比较,若相等,则将链表中的下一个元素与栈中再弹出的元素比较,直至链表尾。这时若栈是空栈,则链表中心对称;否则,当链表中的一个元素与栈中弹出元素不等时,则链表非中心对称,结束算法的执行。
注意:
- 需要注意单链表的元素个数是奇数还是偶数,来处理中间结点。
图解
C实现
核心代码:
/**
* 判断单链表是否对称
* @param list 带头结点的单链表
* @param n 单链表结点个数
* @return 如果单链表对称则返回 1,否则返回 0 表示不对称
*/
int isSymmetry(LNode *list, int n) {
// 0.声明顺序栈,并初始化,用来存放单链表前半个链表中的元素
SeqStack stack;
initStack(&stack);
// 1.用栈存放单链表前半个链表中的元素并同时找到链表的中间结点
// 变量,计算中间结点是单链表中的第几个结点
int count = n / 2;
// 变量,记录链表中的结点,初始为单链表的开始结点
LNode *node = list->next;
// 1.1 循环结束后,node 刚好指向单链表的中间结点
while (count > 0) {
// 1.1.1 用栈存放单链表前半个链表中的元素
push(&stack, node->data);
// 1.1.2 继续单链表的下一个结点
node = node->next;
// 1.1.3 计数器减一
count--;
}
// 1.2 如果单链表结点个数是奇数个,则要前进一步才是单链表后半段的开始结点
if (n % 2 != 0) {
node = node->next;
}
// 2.同时扫描栈和后半段单链表,比较两个值是否相等,如果相等则将栈顶元素出栈和继续单链表的下一个结点
while (!isEmpty(stack) && node != NULL) {
// 2.1 变量,记录栈顶元素值
char top;
getTop(stack, &top);
// 2.2 变量,记录单链表当前结点的数据值
char data;
data = node->data;
// 2.3 如果 top 不等于 data,则表示单链表一定不是对称的,所以直接返回 0 即可
if (top != data) {
return 0;
}
// 2.4 将栈顶元素出栈
pop(&stack, &top);
// 2.5 继续链表的下一个结点
node = node->next;
}
// 3.循环扫描完成后,如果栈中所有元素和单链表后半段所有元素一一对应相等,则表示该单链表是对称的,所以返回 1
return 1;
}
完整代码:
#include 执行结果:
[x, y, z, y, x]
单链表是否对称:1
Java实现
核心代码:
/**
* 判断单链表是否对称
*
* @return 如果单链表是对称的则返回 true,否则返回 false
* @throws Exception 如果顺序栈已满再入栈则抛出此异常
*/
public boolean isSymmetry() throws Exception {
// 0.声明顺序栈,并初始化,用来存放单链表前半个链表中的元素
SeqStack stack = new SeqStack();
stack.init();
// 1.用栈存放单链表前半个链表中的元素并同时找到链表的中间结点
// 变量,记录单链表中的结点个数
int n = size();
// 变量,计算中间结点是单链表中的第几个结点
int count = n / 2;
// 变量,记录链表中的结点,初始为单链表的开始结点
LNode node = list.next;
// 1.1 循环结束后,node 刚好指向单链表的中间结点
while (count > 0) {
// 1.1.1 用栈存放单链表前半个链表中的元素
stack.push(node.data);
// 1.1.2 继续单链表的下一个结点
node = node.next;
// 1.1.3 计数器减一
count--;
}
// 1.2 如果单链表结点个数是奇数个,则要前进一步才是单链表后半段的开始结点
if (n % 2 != 0) {
node = node.next;
}
// 2.同时扫描栈和后半段单链表,比较两个值是否相等,如果相等则将栈顶元素出栈和继续单链表的下一个结点
while (!stack.isEmpty() && node != null) {
// 2.1 变量,记录栈顶元素值
char top;
top = stack.getTop();
// 2.2 变量,记录单链表当前结点的数据值
char data;
data = node.data;
// 2.3 如果 top 不等于 data,则表示单链表一定不是对称的,所以直接返回 0 即可
if (top != data) {
return false;
}
// 2.4 将栈顶元素出栈
stack.pop();
// 2.5 继续链表的下一个结点
node = node.next;
}
// 3.循环扫描完成后,如果栈中所有元素和单链表后半段所有元素一一对应相等,则表示该单链表是对称的,所以返回 1
return true;
}
完整代码:
public class LinkedList {
/**
* 单链表
*/
private LNode list;
/**
* 初始化单链表
*/
public void init() {
// 单链表的初始化分为两步:第一步,创建头结点并分配内存空间;第二步,将头结点的 next 指针指向 null
list = new LNode();
list.next = null;
}
/**
* 通过尾插法创建单链表
*
* @param nums 创建单链表时插入的数据
* @return 创建好的单链表
*/
public LNode createByTail(char... nums) {
// 1.初始化单链表
// 创建链表必须要先初始化链表,也可以选择直接调用 init() 函数
list = new LNode();
list.next = null;
// 尾插法,必须知道链表的尾节点(即链表的最后一个节点),初始时,单链表的头结点就是尾节点
// 因为在单链表中插入节点我们必须知道前驱节点,而头插法中的前驱节点一直是头节点,但尾插法中要在单链表的末尾插入新节点,所以前驱节点一直都是链表的最后一个节点,而链表的最后一个节点由于链表插入新节点会一直变化
LNode tailNode = list;
// 2.循环数组,将所有数依次插入到链表的尾部
for (int i = 0; i < nums.length; i++) {
// 2.1 创建新节点,并指定数据域和指针域
// 2.1.1 创建新节点,为其分配空间
LNode newNode = new LNode();
// 2.1.2 为新节点指定数据域
newNode.data = nums[i];
// 2.1.3 为新节点指定指针域,新节点的指针域初始时设置为 null
newNode.next = null;
// 2.2 将新节点插入到单链表的尾部
// 2.2.1 将链表原尾节点的 next 指针指向新节点
tailNode.next = newNode;
// 2.2.2 将新节点置为新的尾节点
tailNode = newNode;
}
return list;
}
/**
* 判断单链表是否对称
*
* @return 如果单链表是对称的则返回 true,否则返回 false
* @throws Exception 如果顺序栈已满再入栈则抛出此异常
*/
public boolean isSymmetry() throws Exception {
// 0.声明顺序栈,并初始化,用来存放单链表前半个链表中的元素
SeqStack stack = new SeqStack();
stack.init();
// 1.用栈存放单链表前半个链表中的元素并同时找到链表的中间结点
// 变量,记录单链表中的结点个数
int n = size();
// 变量,计算中间结点是单链表中的第几个结点
int count = n / 2;
// 变量,记录链表中的结点,初始为单链表的开始结点
LNode node = list.next;
// 1.1 循环结束后,node 刚好指向单链表的中间结点
while (count > 0) {
// 1.1.1 用栈存放单链表前半个链表中的元素
stack.push(node.data);
// 1.1.2 继续单链表的下一个结点
node = node.next;
// 1.1.3 计数器减一
count--;
}
// 1.2 如果单链表结点个数是奇数个,则要前进一步才是单链表后半段的开始结点
if (n % 2 != 0) {
node = node.next;
}
// 2.同时扫描栈和后半段单链表,比较两个值是否相等,如果相等则将栈顶元素出栈和继续单链表的下一个结点
while (!stack.isEmpty() && node != null) {
// 2.1 变量,记录栈顶元素值
char top;
top = stack.getTop();
// 2.2 变量,记录单链表当前结点的数据值
char data;
data = node.data;
// 2.3 如果 top 不等于 data,则表示单链表一定不是对称的,所以直接返回 0 即可
if (top != data) {
return false;
}
// 2.4 将栈顶元素出栈
stack.pop();
// 2.5 继续链表的下一个结点
node = node.next;
}
// 3.循环扫描完成后,如果栈中所有元素和单链表后半段所有元素一一对应相等,则表示该单链表是对称的,所以返回 1
return true;
}
/**
* 计算单链表的长度,即节点个数
*
* @return 链表节点个数
*/
public int size() {
// 计数器,记录链表的节点个数
int count = 0;
// 链表的第一个节点
LNode node = list.next;
// 循环单链表,统计节点个数
while (node != null) {
// 计数器加1
count++;
// 继续链表的下一个节点
node = node.next;
}
// 返回统计结果
return count;
}
/**
* 打印单链表所有节点
*/
public void print() {
// 链表的第一个节点
LNode node = list.next;
// 循环打印
String str = "[";
while (node != null) {
// 拼接节点的数据域
str += node.data;
// 只要不是最后一个节点,那么就在每个节点的数据域后面添加一个分号,用于分隔字符串
if (node.next != null) {
str += ", ";
}
// 继续链表的下一个节点
node = node.next;
}
str += "]";
// 打印链表
System.out.println(str);
}
}
/**
* 单链表的节点
*/
class LNode {
/**
* 链表的数据域,暂时指定为 int 类型,因为 Java 支持泛型,可以指定为泛型,就能支持更多的类型了
*/
char data;
/**
* 链表的指针域,指向该节点的下一个节点
*/
LNode next;
}
SeqStack:
public class SeqStack {
/**
* 常量,顺序栈所能容纳的最大元素个数
*/
private final int MAXSIZE = 100;
/**
* 声明一个顺序栈
*/
private Stack stack;
/**
* 初始化顺序栈
*/
public void init() {
// 实例化栈对象
stack = new Stack();
// 为数据域分配空间
stack.data = new char[MAXSIZE];
// 将顺序栈的栈顶指针指向 -1 表示空栈
stack.top = -1;
}
/**
* 判断顺序栈是否为空
*
* @return 如果顺序栈为空则返回 true,否则返回 false
*/
public boolean isEmpty() {
// 规定了 -1 表示空栈,所以只需要判断栈顶指针是否等于 -1 即可
return stack.top == -1;
}
/**
* 将指定元素入栈
*
* @param ele 指定元素
* @throws Exception 如果栈满则不能入栈,抛出此异常
*/
public void push(char ele) throws Exception {
// 1.参数校验,如果栈满则不能入栈,抛出异常
if (stack.top == MAXSIZE - 1) {// 因为栈顶指针 top 存储的是数组下标,所以判断是否等于 MAXSIZE-1
throw new Exception("栈已满,不能再插入!");
}
// 2.先栈顶指针加 1,因为原栈顶指针处已经存储了元素,所以加一指向新的空位置
stack.top++;
// 3.在新的空位置处插入新元素,即为指定下标的数组元素赋值
stack.data[stack.top] = ele;
}
/**
* 将栈顶元素出栈
*
* @return 栈顶元素
* @throws Exception 如果栈空则不能出栈,抛出此异常
*/
public char pop() throws Exception {
// 1.参数校验,如果栈空则不能出栈,抛出异常
if (stack.top == -1) {// 因为栈空的定义是栈顶指针为 -1,所以如果栈顶指针为 -1 那么就是空栈,就不能出栈元素
throw new Exception("栈为空,不能出栈元素!");
}
// 2.记录栈顶元素,因为要将该元素返回,即要出栈的元素
char result = stack.data[stack.top];
// 3.栈顶指针减一,因为原栈顶元素已经出栈了,栈中元素个数减一
stack.top--;
return result;
}
/**
* 获取栈顶元素,但不出栈
*
* @return 栈顶元素
* @throws Exception 如果栈空则不能出栈,抛出此异常
*/
public char getTop() throws Exception {
// 1.参数校验,如果栈空则不能出栈,抛出异常
if (stack.top == -1) {
throw new Exception("栈为空,不能获取栈顶元素!");
}
// 2.直接返回栈顶元素,但不出栈
return stack.data[stack.top];
}
/**
* 顺序栈中元素个数
*
* @return 栈中元素个数
*/
public int size() {
// top 表示栈顶指针,实际上就是数组 data 的下标,所以实际元素个数就是下标加一
// 即使是空栈 top=-1,那么最后也会返回 0 表示元素个数为零个
return stack.top + 1;
}
/**
* 打印顺序栈中所有元素,从栈顶到栈底
*/
public void print() {
System.out.print("[");
for (int i = stack.top; i >= 0; i--) {
if (i != stack.top) {
System.out.print(", ");
}
System.out.print(stack.data[i]);
}
System.out.print("]\n");
}
/**
* 清空顺序栈
*/
public void clear() {
// 直接将栈顶指针指向 -1 即可表示空栈,不用重置栈中已有元素的值,因为顺序栈操作只跟栈顶指针有关
stack.top = -1;
}
}
/**
* 栈定义
*/
class Stack {
/**
* 顺序栈用来存储元素的数组
*/
char[] data;
/**
* 记录顺序栈的栈顶指针,即数组下标
*/
int top;
}
测试代码:
public class Test {
public static void main(String[] args) throws Exception {
// 创建单链表并初始化
LinkedList list = new LinkedList();
list.init();
// 为单链表添加测试数据
list.createByTail("xyzyx".toCharArray());
list.print();
// 调用函数,判断单链表是否对称
boolean symmetry = list.isSymmetry();
System.out.println("单链表是否对称:" + symmetry);
}
}
执行结果:
[x, y, z, y, x]
单链表是否对称:true