深度学习笔记(三)——NN网络基础概念(神经元模型,梯度下降,反向传播,张量处理)
文中程序以Tensorflow-2.6.0为例
部分概念包含笔者个人理解,如有遗漏或错误,欢迎评论或私信指正。
截图部分引用自北京大学机器学习公开课
人工智能算法的主流分类
首先明白一个概念,广义上的人工智能算法并不是只有Machine Learning或Deep Learning,而是一个相对的,能够使用计算机模拟人类智能在一定场景下自动实现一些功能。所以系统控制论中的很多最优控制算法同样可以称之为智能算法。在后面的描述中我们会看到NN结构在学习参数的过程中其实很类似于一个通过反馈系统,能自动矫正控制器参数的控制系统。
首先,学界将算法分类为以下三种主要类型:
行为主义,构建感知控制系统(控制论,经典控制论或者现代控制理论中的各种矫正模型和最优控制算法也属于智能控制算法的一种)
符号主义,基于数学表达和运算求解(通过数学建模,将复杂问题转化为完整的数学系统,通过数学方法求出解,进而解决问题,例如专家系统)
连接主义,基于仿生学,构建类神经网络,神经网络模型则类似于黑盒性质,通过自动的学习和参数调整,可以实现对复杂非线性方程的描述。
传统的建模方法和控制理论已经发展的非常完善,但是依然在实际应用中存在局限性。基于网络模型的算法,通过学习可以快速的拟合各类复杂的非线性函数,并且在数学设计上相比众多建模方法原理简单明了,便于设计和使用。
认识神经网络
通常构建一个NN网络我们需要以下内容:
1、什么是神经元模型
在中学生物中学习过生物神经元,包含树突,轴突,胞体等结构,大量的神经元细胞之间可以相互连接。同样可以在计算机中模拟出单一神经元的MP模型:
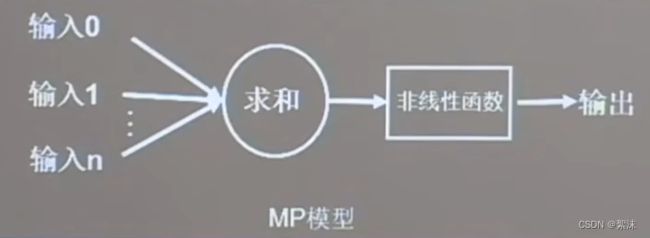
对于这样的单个神经元模型,当输入多个来源的数据,通过每个输入乘以各自权重系数后求和,在经由一些特定的输出函数后得到结果。可以写成向量函数: Y = F ( X × Y + b ) \mathit{Y=F(X\times Y+b)} Y=F(X×Y+b)其中Y是输出,X是输入,W是网络权重,b是偏置系数,f是输出函数
假设我们有很多个神经元,他们彼此连接,用多个上面的神经元模型并列就可以构成一层神经网络,再使用多层神经网络级联就可以更加复杂的网络结构。那么我们就可以一定的权重参数下计算输入对应的特地输出

上面的例子中输入4个X,输出3个Y,特定的输入会对应特定的输出。这个输出的数据就可以进一步设计,通过判断来得到最后总共的结果。
2、常见的神经网络构建流程:
- 准备数据:准备大量的“特征\标签”数据 ,网络通过学习二者之间的差距,来修改权重参数
- 搭建网络结构,设计特定的网络层连接
- 通过反向传播训练网络,优化参数
- 保存模型,使用前向传播推理计算结果
通常的分类问题中,大多数都可以数学建模使用判别式的计算来实现目标结果。但是数学建模和判别的计算会随着问题的复杂而不断复杂化,所以上述流程的NN网络算法就显得简单明了,容易使用。
3、模型的训练
在简单的MLP模型中,假设网络中每个权重都首次赋予某个初值,输入数据后进行一次计算,会得到第一次的输出,此时该输出与输入的标签之间会存在差距。利用损失函数来计算输出Y和正确标签之间的差距,通过反向传播(反馈修正)更改网络中的权重系数。在损失函数的计算中,当损失函数的输出值loss最小时,网络中的权重和偏置系数达到了最优值。
所以模型的训练过程可以理解为:输入一组数据,通过一次前向推理得到计算结果,损失函数计算标注数据和推理结果的差距,计算损失函数当前的梯度下降方向,按照梯度下降方向反过来修改网络中的权重参数,保存网络,再重复上述过程。直到最后网络输出的结果已经能够足够精准的预测输出停止。这个反复的过程就称之为网络的训练。在训练的过程中循环的次数称之为迭代次数Epoch ,一次循环中输入网络的数据量大小称之为batch_size。其中Epoch 影响训练时间的长短,batch_size过大则需要更大的显存来训练。
简化的流程图可以理解为:(这里忽略输入和输出环节的其它步骤)

实际的应用中data在输入之前会经过一定的预处理和分组,输出也会由不同的设计来实现特定的目的。
4、反向传播在做什么:
理解反向传播之前,我们需要清楚前向传播在做什么,通常在前向传播的过程中,我们直接给网络输入一组数据,让网络计算得到结果,就完成了一次前向传播。在训练的过程中依次完整的训练是包含一次前向传播+一次反向传播+参数修改完成的(这里暂时忽略一些重要的细节),训练完成后,使用权重模型来推理预测的过程,就是单次的前向传播。
所以权重成为了至关重要的数据,修改权重就是让网络学习数据输入到输出的映射关系,故而设计反向传播,通过输出的数据反过来修正权重参数。
在反向传播的过程中,人们设计了损失函数来表达计算结果和实际结果之间的误差。通过损失函数量化了输出误差的计算,使得计算机能够自动进行反向矫正。使得修改权重参数的问题转化为:如何能让输出的损失函数值变的更小。
回顾梯度的定义:函数对参数求偏导数,梯度减小的方向就是函数减小的方向,就是函数的最大方向向量。沿着函数梯度下降的方向就可以使损失函数输出变小。
所以可以利用计算损失函数梯度下降的方向来寻找权重修改的方向,来计算得到损失函数的最小值。
在梯度下降法中: 权重参数的计算:

式中,lr是学习率,是一个超参数。学习率较大时,W的更新幅度较快,学习率过小时W更新幅度较小,Floss就是损失函数。通过一次次的迭代,最终可以得到一个使输出Loss最小的W。最常用的损失函数有均方误差:MSE

MSE直接计算Y和I之间每个数据点之间的差之和并最后求平均。
5、反向传播——梯度下降
上面已经介绍了我们希望使用梯度下降来找到合适的权重参数W,来使得损失函数的输出能够最小。由于梯度减小的方向就是函数减小的方向,所以可以使用梯度下降法来计算最优参数。
在基础的神经元模型中包含权重参数w,偏置系数b,y的输出取决于w和b共同作用。

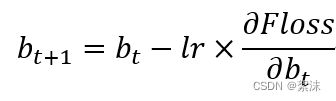

在梯度下降的公式中学习率lr显得十分重要,当学习率设置的太小时,收敛将变得十分缓慢,等学习率变得过大时梯度的值可能在最小值之间来回震荡,导致无法收敛。

在反向传播的过程中,算法会从前向后,一层一层的用损失函数计算每层参数的偏导数,并根据结果更新这层的所有参数。
6、张量的概念
我们知道神经网络的计算中每个输入是由矩阵形式的数据构成的,为了便于网络计算以及使用统一框架,我们需要使用tensorflow中提供的张量模型。张量其实质上就是一个多维数组。数组的维数就是张量的阶数,一个0阶的数称为标量(scalar),1阶数组称为向量,二阶数组称为矩阵,三阶及以上的数组称为张量。
张量中的数量型数据类型常见的有三种: tf.int32 ,tf.float32 , tf.float64
此外还有数以外的数据类型,如 布尔型 tf.bool , 字符串型 tf.string
# (执行代码前请先关注下文的程序版本)创建一个张量:
# tf.constant(内容,dtype=数据类型)
num = tf.constant([1,2], dtype=tf.int64) # 数
usr_bool = tf.constant([True]) · # 布尔 or: tf.constant([False])
usr_string = tf.constant("Hello world!") # 字符串
通常来说我们会从numpy中导入数据到tensor:
a = np.arange(0, 5)
b = tf.convert_to_tensor(a, dtype=tf.int64)
print(a)
print(b)
得到输出:
[0 1 2 3 4]
tf.Tensor([0 1 2 3 4], shape=(5,), dtype=int64)
其中a为一行5列,b为1行5列,shape表示维度,dtype表示数据类型
当然我们也可以从头创建Tensor:
a1 = tf.zeros(3) # 全零型,一阶
a2 = tf.ones([3,3]) # 全1型,二阶
a3 = tf.fill([3,3,3], 3) # 指定数值,三阶
print(a1, a2, a3)
在创建张量时,维度格式按照:一维直接写个数,二维用[行数,列数] ,多维就用[n,m,,j,k,l......]
有时候我们还会需要一些随机数来作为初始张量,这个随机数一般希望他是符合正态分布(高斯分布)或者均匀分布的:
a1 = tf.random.normal([2,2], mean=0, stddev=1) # 生成正态分布随机数张量,输入参数:维度,均值,标准差
a2 = tf.random.truncated_normal([2,2], mean=0, stddev=1) # 生成截断式正态分布随机数张量,输入参数:维度,均值,标准差,输出数据均在mean±2*stddev之内
print(a1, a2)
正态分布服从:
Φ ( μ , δ ) = 1 2 π δ × e − ( x − μ ) 2 2 δ \Phi (\mu ,\delta )=\frac{1}{\sqrt{2\pi } \delta} \times e^{-\frac{{(x-\mu)^2} }{2 \delta} } Φ(μ,δ)=2πδ1×e−2δ(x−μ)2
梯度下降计算程序演示
程序环境
cuda = 11.2
python=3.7
numpy==1.19.5
matplotlib== 3.5.3
notebook==6.4.12
tensorflow==2.6.0
在下面的程序中我们手动创建一个值为5的张量,并且设置损失函数为
f ( x ) = ( x + 1 ) 2 \ f(x)=(x+1)^{2} f(x)=(x+1)2
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots()
# 定义变量
lr = [0.6, 0.2, 0.01] # 设置了三个学习率
epoch = 50 # 迭代50次
losses = []
for lrs in lr:
wegt = tf.Variable(tf.constant(5, dtype=tf.float32)) # 定义了值为5,数据类型为float32
for epoch in range(epoch):
with tf.GradientTape() as tape: # 创建上下文管理器,用于记录网络训练的过程
loss = tf.square(wegt + 1) # 计算损失函数的值,在tf.GradientTape上下文中,损失函数是loss = (wegt + 1)的平方
grads = tape.gradient(loss, wegt) # 利用上下文管理器记录的信息,gradient()函数自动求微分,计算损失相对于权重 wegt 的梯度
wegt.assign_sub(lrs * grads) # 跟新权重:assign_sub()函数等效是自减=> wegt=wegt-lr * grads
print("After %s epoch, w is %f, loss is %f" % (epoch, wegt.numpy(), loss))
losses.append(loss.numpy())
ax.plot(np.arange(0, epoch + 1, 1), losses, label="lr={}".format(lrs))
losses.clear()
ax.set(xlabel='Epoch', ylabel='Loss', title='Gradient Descent')
ax.legend(loc='upper right')
ax.grid()
plt.show()
可以看到计算得到的wegt权重值不断缩小,loss不断接近于0,且学习率越小w收敛的速度越慢。当然还可以尝试将学习率改为0.99,会看到学习率过大的时候w参数同样不容易稳定下来。
