BFS题目专栏

1091. 二进制矩阵中的最短路径

题目来自leetcode

给你一个 n x n 的二进制矩阵 grid 中，返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径，返回 -1 。
二进制矩阵中的畅通路径是一条从 左上角 单元格（即(0, 0)）到 右下角 单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

路径途经的所有单元格都的值都是 0 。
路径中所有相邻的单元格应当在 8 个方向之一 上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。
畅通路径的长度 是该路径途经的单元格总数。

示例 1：

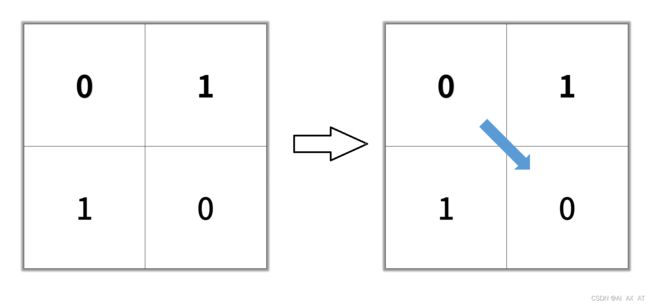
输入：grid = [[0,1],[1,0]]
输出：2

示例 2：

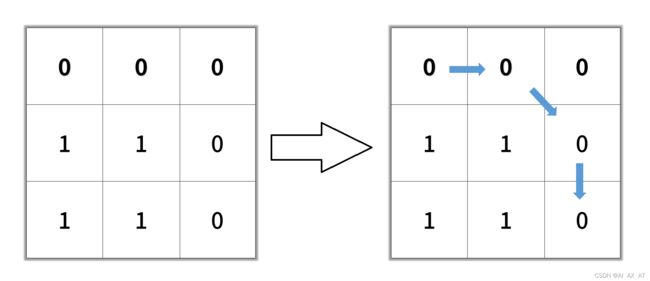
输入：grid = [[0,0,0],[1,1,0],[1,1,0]]
输出：4

示例 3：
输入：grid = [[1,0,0],[1,1,0],[1,1,0]]
输出：-1

提示：
n == grid.length
n == grid[i].length
1 <= n <= 100
grid[i][j] 为 0 或 1

思路：

1. 每次搜寻所在位置周围八个位置是否为0，0则入队，1则不做处理，找完周围所有为0的位置后步数加1。这样走完一步，一定要想清楚。

代码：

class Solution:
    def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
        # 典型的bfs题目，循环访问每一层未访问过的点，只有访问完这一层的点才会访问下一层
        # 矩阵行数
        row = len(grid)
        # 矩阵列数
        col = len(grid[0])
        # 如果矩阵大小为1且初始值为0则步数只有1
        if row == 1 and col == 1 and grid[0][0] == 0:
            return 1
        # 如果矩阵入口为1或者出口为1，无论如何是走不了的，返回-1
        if grid[0][0] == 1 or grid[-1][-1] == 1:
            return -1
        # 记录步数
        step = 1
        # 创建队列，存储未访问的点
        queue = [(0,0)]
        # 标记入口已访问过
        grid[0][0] = 1
        # 循环访问队列未访问过点
        while queue:
            # 队列长度
            current_len = len(queue)
            # 循环访问队列
            for _ in range(current_len):
                # 取队列队首的值
                i,j = queue.pop(0)
                # 循环取上、下、左、右、左上、右上、左下和右下八个位置
                for x,y in [(0,1),(0,-1),(1,0),(-1,0),(1,1),(1,-1),(-1,-1),(-1,1)]:
                    temp_i = i + x
                    temp_j = j + y
                    # 判断是否溢出矩阵范围
                    if 0 <= temp_i < row and 0 <= temp_j < col:
                        # 判断是否已经到达终点
                        if temp_i == row-1 and temp_j == col-1:
                            return step + 1
                        # 如果遇到障碍，不做处理，继续寻找周围的0
                        if grid[temp_i][temp_j] == 1:
                            continue
                        # 如果此方格为0，则可以通行，同时为防止重复访问，已访问的赋值为1
                        if grid[temp_i][temp_j] == 0:
                            grid[temp_i][temp_j] = 1
                            queue.append((temp_i,temp_j))
            # 无论如何，循环一次就走一步
            step +=1
        # 到最后如果都没有找到出口，返回-1
        return -1

200. 岛屿数量

题目来自leetcode

给你一个由 **‘1’（陆地）和 ‘0’（水）**组成的的二维网格，请你计算网格中岛屿的数量。
岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外，你可以假设该网格的四条边均被水包围。

示例 1：
输入：grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出：1

示例 2：
输入：grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出：3

提示：
m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’

思路：

1. 连成一片1的代表一个小岛
2. 一个小岛一个小岛的遍历
3. 遍历过的1要赋值0

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        # 创建队列，用于存储未访问过的1的坐标
        queue = []
        # 小岛数量
        island = 0
        # 行数
        row = len(grid)
        # 列数
        col = len(grid[0])
        # 循环寻找二维数组每个小岛
        for i in range(row):
            for j in range(col):
                # 找到某小岛第一个1
                if grid[i][j] == "1":
                    # 访问过赋值0
                    grid[i][j] = "0"
                    # 小岛数量加1
                    island = island + 1
                    # 添加1的坐标到队列
                    queue.append((i,j))
                    # 循环队列，找出同一小岛的所有1
                    while queue:
                        # 取出队首坐标
                        n,m = queue.pop(0)
                        # 寻找上下左右是否为1
                        for x,y in [(1,0),(-1,0),(0,1),(0,-1)]:
                            # x坐标
                            temp_i = n + x
                            # y坐标
                            temp_j = m + y
                            # 防止数组越界
                            if 0 <= temp_i < row and 0 <= temp_j < col:
                                # 1周围的1
                                if grid[temp_i][temp_j] == "1":
                                    # 访问过的1赋值为0
                                    grid[temp_i][temp_j] = "0"
                                    # 1周围的1的坐标添加到队列
                                    queue.append((temp_i,temp_j))
        return island
                        

全球变暖

题目描述
你有一张某海域 NxN 像素的照片，".“表示海洋、”#"表示陆地，如下所示：

.......
.##....
.##....
....##.
..####.
...###.
.......

其中 上下左右 四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有 2 座岛屿。
由于全球变暖导致了海面上升，科学家预测未来几十年，岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋)，它就会被淹没。

例如上图中的海域未来会变成如下样子：

.......
.......
.......
.......
....#..
.......
.......

请你计算：依照科学家的预测，照片中有多少岛屿会被完全淹没。

输入描述
第一行包含一个整数 N(1≤N≤1000)。
以下 N 行 N 列代表一张海域照片。
照片保证第 1 行、第 1 列、第 N 行、第 N 列的像素都是海洋。
输出一个整数表示答案。

输入输出样例
示例
输入

7
.......
.##....
.##....
....##.
..####.
...###.
.......

输出
1

Notes：

1. 利用BFS宽搜的思想求解宽搜

import os
import sys


# 海域长宽
n = int(input())
# 存储字符
sea = []
# 标记有不会被淹没的小岛
land = 0
# 小岛数量
island = 0
# 没有被淹没的小岛数量
count = 0
# 创建队列
queue = []
# 输入每行字符
for _ in range(n):
    sea.append(list(map(str,input())))

for i in range(n):
    for j in range(n):
      # 初始化为0，表示已淹没
        land = 0
        # 找到一个小岛
        if sea[i][j] == '#':
            island += 1
            queue.append((i,j))
            # 已访问过的赋值为*
            sea[i][j] = '*'
            # 循环一个小岛上所有#
            while queue:
              # 取队首
                a,b = queue.pop(0)
                # 循环上下左右是否为#
                for x,y in [(0,-1),(0,1),(-1,0),(1,0)]:
                    temp_i = a + x
                    temp_j = b + y
                    if 0 <= temp_i < n and 0 <= temp_j < n:
                        if sea[temp_i][temp_j] == '#':
                          # 周围没有.，表示此小岛没有被淹没
                            if (0 <= temp_j - 1 < n and sea[temp_i][temp_j-1] != '.') and (0 <= temp_j + 1 < n and sea[temp_i][temp_j+1] != '.') and (0 <= temp_i - 1 < n and sea[temp_i-1][temp_j] != '.') and (0 <= temp_i + 1 < n and sea[temp_i+1][temp_j] != '.'):
                                land = 1
                            queue.append((temp_i,temp_j))
                            sea[temp_i][temp_j] = '*'
            # 没有被淹没的小岛数量加1
            if land == 1:
                count += 1
print(island-count)