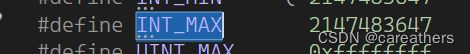【C语言】详解C语言二分查找逻辑及其代码实现

  在一个有序的数组中，当我们想要快速地查找到某个数字时，可以采用逐一对照的方式，可是这种方法的效率是非常慢的，于是我们迫切地需要一种便捷高效的方式来解决这个问题，于是本文的主题“二分查找”便应运而生了。

  适用场景

必须为有序数组，不论升序或是倒序。

  二分查找实现逻辑

 接下来我便以下题为例来进行讲解：

例：在有序数组1~10中找到数字7

  (arr为数组名)

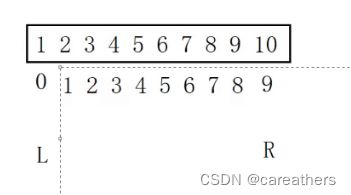
  当我们使用二分查找时，需要先找到最左边与最右边的下标，设为left和right（以下简称L,R）

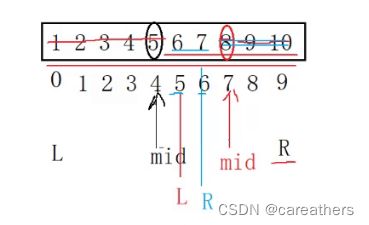
  在这个例子中L=0,R=9

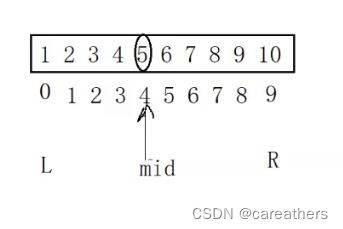
  此时我们设定中间数mid=(L+R)/2，通过arr[mid]与数字7进行比较

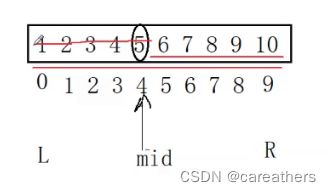
 很显然因为mid=（0+9）/2=4，而arr[4]=5 < 7，故mid往左的下标均不用考虑

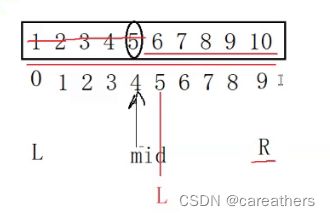
右下标R的值不要变，左下标L的值变为mid+1，也就是说我们只需要在下标5，6，7，8，9中筛选

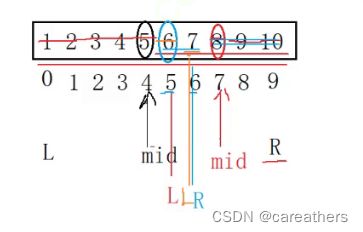
 此时mid=（5+9）/2=7，而arr[7]=8 > 7,故mid往右的下标均不用考虑

 左下标L的值不要变，右下标R的值变为mid-1，也就是说我们只需要在下标5，6中筛选

 此时mid=（5+6）/2=5，而arr[5]=6 < 7,此时剩余的被查找数只剩下下标6

 

 右下标R的值不要变，左下标L的值变为mid+1，mid=（6+6）/2=6,而arr[6]=7 = 7，我们便找到了数字7。

  不难看到，我们每次查找都是通过左右元素的下标求出中间元素的下标，再用中间元素的下标锁定元素再和我们想要查找的值相比较，不论是大了或者小了，我们都可以去除另外一半，每查去掉一半便锁定了新的范围，再在新的范围内使用二分查找，这样我们可以很快地找到想要的元素，或者找不到。

代码实现

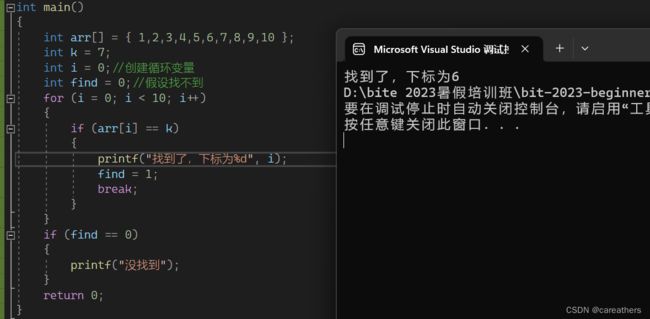
  实现方式一，逐一对照查找：

#include 
int main()
{
int arr[] = {1,2,3,4,5,6,7,8,9,10};
int k = 7;
int i = 0;//创建循环变量
int find = 0;//假设找不到
for(i = 0; i < 10; i++)
{
  if(arr[i] == k)
    {
    printf("找到了,下标为%d"， i);
    find = 1;
    break;
    }
}
if(find == 0)
{
printf("没找到");
}
return 0;
}

输出结果：

  实现方式二，二分查找： 

#include 

int main()
{
int arr[] = {1,2,3,4,5,6,7,8,9,10};
int k = 0;
scanf("%d", &k);//7
int left = 0;
int right = sizeof(arr)/sizeof(arr[0]) - 1;//注释1
int find = 0;
while(left <= right)
  {
  int mid = left + (right - left)/2;//注释2
  if(arr[mid] > k)

    right = mid -1;

  else if(arr[mid < k])

    left = mid + 1;

  else
    {
    printf("找到了，下标为%d", mid);
    find = 1;
    break;
    }
  }
if(find == 0)
  printf("没找到");
return 0;
}

注释一：计算元素个数代码实现

  当我们想要求一个数组中元素的个数时，不必再去数数组中的元素，而是可以通过更通解的方式来解决。

  可以看到该段代码：

sizeof(arr) / sizeof(arr[0]);

  意为使用 数组内存大小/单个元素内存大小，即可计算出元素个数；

  以后在代码中需要数组元素个数的地⽅就不⽤固定写死了，使⽤上⾯的计算，不管数组怎么变化，计算出的⼤⼩也就随着变化了。

注释二：求平均数优解

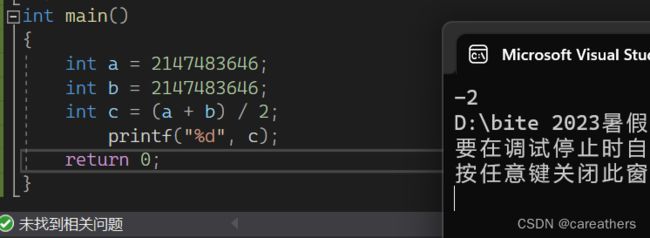
  在看到L与R求平均数时，可能部分朋友习惯于数学中的方式：（L+R）/2，但是在C语言中，int是有最大值的，如下：

若是值超出这个范围，会导致计算出现问题，如下：

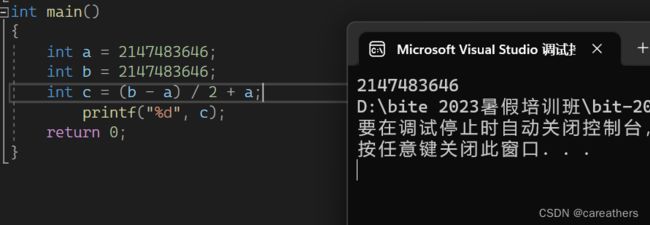
 而该段代码可以最大限度避免该情况发生：

int mid = left + (right - left)/2;

代码实现如下：

  本次的分享到此为止啦，谢谢大家观看，期待我们的下次见面！