哈夫曼树编码、译码---(c语言实现)
1.上面是哈夫曼树?
1.1为什么要有哈夫曼树?
先提出一个例子,加入现在有一串长度为8万的字符串,这些字符串全都由a、b、c、d、e和f,这六个字母组成。那么如何将这8万个字母组成的字符串转化为编码呢?最简易的编码方式肯定是将a编码000,b编码001,c编码010,d编码011,e编码110,f编码101,这样一来每个这整个字符串的长度就要占用3*80000=24万个比特位,对于这样的固定长度编码,每一个字符所占空间都是一样的,那么我们是否可以通过可变长度编码方式来实现节省空间呢?
这就要提到我们的哈夫曼树编码了
1.2怎样进行哈夫曼编码呢?
当我们开始对字符串进行可变长度编码时,我们需要统计出这些字符串中每个字母出现的次数,与之相对应的就是,出现次数最多的我们用长度最短的编码表示,出现次数最多的我们用可编码长度最长来表示,这样就可以实现我们的可编码长度。
比如将上面的a、b、c、d、e和f分别出现3.2 1.6 0.8 0.7 0.6 1.1万次,我们将其编码为a=0 b=10 c=1110 d=10 e=1111 f=110现在我们再次计算他们的字符串长度:3.2*1+2*1.6+0.8*4+2*0.7+4*0.6+3*1.1=16.7。当我们这样编码的时候就已经少编码了7万多个比特位。(实际上这已经是最优情况了,下面会解释)
为什么要按照上面的形式编码呢?其实编码的形式不唯一,但要遵守一个原则,没有一个编码是其他编码的前缀,为什么要遵守这个原则呢?
加入我们将a的编码编码为1,那么ab组成的编码为110,当我们开始译码的时候,我们会发现,110即可译码为ab,也可以译码为f,所以这个时候就和我们的编码相冲突了,译码时有多选择,不唯一。但是当每一个字符的编码不是其他编码的前缀时,就不会出现这样的状况了,这时的编码长度就已经唯一了。
以下是我们将我们构建的树进行可视化,(0表示左子树,1表示右子树)
由图中可以看出,可变长度编码为 树为一颗满二叉树(当然形式不固定),而固定长度的编码却不是满二叉树,仅仅只是一颗普通的二叉树
对于满二叉树,它的带权路径为最小,所以我们可以得出的编码数量和最小值。
带权路径:从根到结点之间路劲的长度与结点上的权值的乘积
2.哈夫曼树代码
先给出代码,下面会对代码进行解释。
注:代码一为仅由权重而建立的哈夫曼树(本篇只解析了这个),代码二可以输入相应字符以及字符对应的权重而建树(这段代码和以上代码只做了部分修改,逻辑不变)
注:以下代码是在CLion 2023.2.2语言环境中编辑的,若在其他环境中,可能会有警告,但都大同小异,改一下就好了。
2.1代码
2.1.1代码一
#include
#include
#include
#include
#define ElemType int
typedef struct Node{
ElemType weight;
int parent,left,right;
}HTNode,*HuffmanTree; //哈夫曼树结构
typedef char **HuffmanCode; //动态内存分配huffman编码,二元数组指针
void Selection(HuffmanTree HT,int n,int* s1,int* s2);
void write_HuffmanTree(HuffmanTree HT,int n); //将哈夫曼树以前序遍历的形式写入文件中
void Transform_Coding(HuffmanTree HT,int n);
void write_CodeFile(HuffmanCode HC,int n);
void HuffmanCoding(HuffmanTree HT,HuffmanCode HC,const int* w,int n);
int main(){
int w[8]={5,29,7,8,14,23,3,11}; //测试值
int n=8;
HuffmanTree HT=NULL;
HuffmanCode HC=NULL;
HuffmanCoding(HT,HC,w,n);
return 0;
}
void write_CodeFile(HuffmanCode HC,int n){
FILE* file= fopen("CodeFile.txt","w");
if(file==NULL){
printf("%s\n", strerror(errno)); //若文件打开失败,打印出出问题的情况
assert(file!=NULL); //断言,进入这个循环则停止程序
}
int i;
for(i=1;i<=n;i++){
fprintf(file,"%s ",HC[i]);
}
fclose(file);
file=NULL;
}
//将哈夫曼树以前序遍历的形式写入文件中
void write_HuffmanTree(HuffmanTree HT,int n){
FILE* file= fopen("hfmTree.txt","w");
if(file==NULL){
printf("%s\n", strerror(errno));
return;
}
//将HC中的写入文件中
int i;
fprintf(file,"%s\t%s\t%s\t%s\n","weight","parent","left","right");
for(i=1;i<=2*n-1;i++){
fprintf(file, "%-6d\t%-6d\t%-4d\t%-5d\n",HT[i].weight,HT[i].parent,HT[i].left,HT[i].right);
}
fclose(file);
file=NULL;
}
void Selection(HuffmanTree HT,int n,int* s1,int* s2){
//找到HT[1...i-1]中parent为0且weight最小的两个结点
int i;
int a1,a2; //用a来记住最小权重的位置
a1=a2=-1;
for(i=0;i<=n;i++){
if(HT[i].parent==0){
if(a1==-1||HT[i].weightright=0;
p->left=0;
p->weight=0;
p->parent=0;
}
for(p=HT+1,i=1;i<=n;++p,++i,++w){ //初始化权重
p->weight=*w;
}
//写一个权重挑选函数
for(i=n+1;i<=m+1;++i){
int S1,S2;
Selection(HT,i-1,&S1,&S2); //找到两个最小的结点,并不能找到对应的最小值的位置
HT[i].weight=HT[S1].weight+HT[S2].weight;//此结点的权重为S1+S2的权重
HT[S1].parent=HT[S2].parent=i; //更新最小两个结点的双亲结点
HT[i].left=S1;
HT[i].right=S2; //更新孩子结点
}
//需要对编写的哈夫曼树进行写入文件
HT[15].parent=0; //将根节点的父亲结点,设置为0,便于之后进行编码的时候搜索到根节点,不至于报错Segmentation fault
write_HuffmanTree(HT,n); //写如文件操作
HC=(HuffmanCode) malloc((n+1)*sizeof (char*)); //给二维数组指针进行分配空间
if(HC==NULL)printf("%s\n", strerror(errno)); //判断是否分配失败
assert(HC!=NULL); //断言!阻止程序进行运行下去
char* coding=(char*) malloc(n*sizeof (char)); //分配编码空间
if(coding==NULL)printf("%s\n", strerror(errno)); //判断是否分配失败
assert(coding!=NULL); //阻止程序进行运行下去
//从叶子结点到根逆向求解出每个字符的HUFFMAN编码
coding[n-1]='\0'; //最后一个字符为编码结束符号
for(i=1;i<=n;i++){
int start=n-1; //用于coding[]的动态存储
int thread;
int current;
//当i=15的时候,并不能直接找到15的结点,当i等于15的时候直接跳出这一次到下一次循环
if (i > n) {
continue;
}
for(current=i,thread=HT[i].parent;thread!=0;current=thread,thread=HT[thread].parent){
if(HT[thread].left==current){ //若是左孩子,则编码为0
coding[--start]='0';
} else{
coding[--start]='1';
}
}
HC[i]=(char*) malloc((n-start)*sizeof (char)); //为第i个字符编码分配空间,刚好可以分配出需要的编码空间
strcpy(HC[i],&coding[start]); //将字符串拷贝
}
write_CodeFile(HC,n); //编码进去
Transform_Coding(HT,n);
free(coding); //释放原来的空间
free(HC);
free(HT);
HC=NULL;
HT=NULL;
} //创建哈夫曼树,并且编码哈夫曼树
//编辑译码函数,针对上面的HC[],我们需要将编码与HC[]对应起来,看是第几个,找出其中的i,然后打印对应的HT[i]
//涉及到子串的问题
void Transform_Coding(HuffmanTree HT,int n){
FILE* pf_read= fopen("CodeFile.txt","r");
FILE* pf_write= fopen("TextFile.txt","w");
if(pf_read==NULL||pf_write==NULL){
printf("%s\n", strerror(errno));
assert(pf_write!=NULL);
assert(pf_read!=NULL);
}
char buffer[100]; //存储从文件读取的二进制码
fgets(buffer, sizeof(buffer),pf_read);//读到文件
int current=2*n-1; //直接指向根结点
int i=0;
while (buffer[i]!='\0'){ //直到当前二进制字符串结束,跳出循环,译码结束
if(buffer[i]=='0'){
current=HT[current].left; //左子树移动,根据之前编码的情况进行选择
} else if(buffer[i]=='1'){
current=HT[current].right; //右子树移动
}
if(HT[current].left==0&&HT[current].right==0){ //孩子结点都为0.说明已经走到叶子结点
fprintf(pf_write, "%d ", HT[current].weight);
current=2*n-1; //重置根结点,以便继续解码
}
i++;
}
fclose(pf_read); //关闭文件
fclose(pf_write);
pf_write=NULL; //置为NULL
pf_read=NULL;
} 2.1.2代码二
#include
#include
#include
#include
#define ElemType char
typedef struct Node{
ElemType character;
int weight;
int parent,left,right;
}HTNode,*HuffmanTree; //哈夫曼树结构
typedef char **HuffmanCode; //动态内存分配huffman编码,二元数组指针
void Selection(HuffmanTree HT,int n,int* s1,int* s2);
void write_HuffmanTree(HuffmanTree HT,int n); //将哈夫曼树以前序遍历的形式写入文件中
void Transform_Coding(HuffmanTree HT,int n);
void write_CodeFile(HuffmanCode HC,int n);
void HuffmanCoding(HuffmanTree HT,HuffmanCode HC,const HTNode* w,int n);
void menu();
//输入一系列的字符串,以及对应的权重
//编码还是按照原始来编码,那么在写入文件的时候,就是写入权值
int main(){
int capacity=3; //默认分配的数组空间
int size=0; //当前已用的数组空间
HTNode* w = (HTNode*)malloc(capacity * sizeof(HTNode)); //分配默认空间
if (w == NULL) {
printf("%s", strerror(errno));
exit(1);
}
int i=0;
do {
menu();
scanf_s(" %c %d", &w[i].character, sizeof(w[i].character), &w[i].weight); //输入字符以及对应的权值
size += 1; //计数
if (size == capacity) { //如果数组空间不够,扩充一倍
capacity *= 2;
HTNode *temp = (HTNode*)realloc(w, capacity * sizeof(HTNode));
if (temp == NULL) { // 如果重新分配失败,则直接退出程序
printf("%s", strerror(errno));
free(w); //释放之前已分配的内存
exit(1);
}
w = temp;
}
i+=1;
} while (w[i-1].character != '-');
int n=size-1;
HuffmanTree HT=NULL;
HuffmanCode HC=NULL;
HuffmanCoding(HT,HC,w,n);
return 0;
}
void menu(){
printf("Please input the char and weight(enter -1 to leave):");
}
void write_CodeFile(HuffmanCode HC,int n){
FILE* file= fopen("CodeFile.txt","w");
if(file==NULL){
printf("%s\n", strerror(errno)); //若文件打开失败,打印出出问题的情况
assert(file!=NULL); //断言,进入这个循环则停止程序
}
int i;
for(i=1;i<=n;i++){
fprintf(file,"%s ",HC[i]);
}
fclose(file);
file=NULL;
}
//将哈夫曼树以前序遍历的形式写入文件中
void write_HuffmanTree(HuffmanTree HT,int n){
FILE* file= fopen("hfmTree.txt","w");
if(file==NULL){
printf("%s\n", strerror(errno));
return;
}
//将HC中的写入文件中
int i;
fprintf(file,"%s\t%s\t%s\t%s\t%s\n","char","weight","parent","left","right");
for(i=1;i<=2*n-1;i++){
fprintf(file, "%-4c\t%-6d\t%-6d\t%-4d\t%-5d\n",HT[i].character,HT[i].weight,HT[i].parent,HT[i].left,HT[i].right);
}
fclose(file);
file=NULL;
}
void Selection(HuffmanTree HT,int n,int* s1,int* s2){
//找到HT[1...i-1]中parent为0且weight最小的两个结点
int i;
int a1,a2; //用a来记住最小权重的位置
a1=a2=-1;
for(i=0;i<=n;i++){
if(HT[i].parent==0){
if(a1==-1||HT[i].weightright=0;
p->left=0;
p->weight=0;
p->parent=0;
p->character='0';
}
for(p=HT+1,i=1;i<=n;++p,++i,++w){ //初始化权重
p->weight=w->weight;
p->character=w->character;
}
//写一个权重挑选函数
for(i=n+1;i<=m;++i){
int S1,S2;
Selection(HT,i-1,&S1,&S2); //找到两个最小的结点,并不能找到对应的最小值的位置
HT[i].weight=HT[S1].weight+HT[S2].weight;//此结点的权重为S1+S2的权重
HT[S1].parent=HT[S2].parent=i; //更新最小两个结点的双亲结点
HT[i].character='#';
HT[i].left=S1;
HT[i].right=S2; //更新孩子结点
}
//需要对编写的哈夫曼树进行写入文件
write_HuffmanTree(HT,n); //写如文件操作
HC=(HuffmanCode) malloc((n+1)*sizeof (char*)); //给二维数组指针进行分配空间
if(HC==NULL)printf("%s\n", strerror(errno)); //判断是否分配失败
assert(HC!=NULL); //断言!阻止程序进行运行下去
char* coding=(char*) malloc(n*sizeof (char)); //分配编码空间
if(coding==NULL)printf("%s\n", strerror(errno)); //判断是否分配失败
assert(coding!=NULL); //阻止程序进行运行下去
//从叶子结点到根逆向求解出每个字符的HUFFMAN编码
coding[n-1]='\0'; //最后一个字符为编码结束符号
for(i=1;i<=n;i++){
int start=n-1; //用于coding[]的动态存储
int thread;
int current;
//当i=15的时候,并不能直接找到15的结点,当i等于15的时候直接跳出这一次到下一次循环
if (i > n) {
continue;
}
for(current=i,thread=HT[i].parent;thread!=0;current=thread,thread=HT[thread].parent){
if(HT[thread].left==current){ //若是左孩子,则编码为0
coding[--start]='0';
} else{
coding[--start]='1';
}
}
HC[i]=(char*) malloc((n-start)*sizeof (char)); //为第i个字符编码分配空间,刚好可以分配出需要的编码空间
strcpy(HC[i],&coding[start]); //将字符串拷贝
}
write_CodeFile(HC,n); //编码进去
Transform_Coding(HT,n);
free(coding); //释放原来的空间
free(HC);
HC=NULL;
HT=NULL;
} //创建哈夫曼树,并且编码哈夫曼树
//编辑译码函数,针对上面的HC[],我们需要将编码与HC[]对应起来,看是第几个,找出其中的i,然后打印对应的HT[i]
//涉及到子串的问题
void Transform_Coding(HuffmanTree HT,int n){
FILE* pf_read= fopen("CodeFile.txt","r");
FILE* pf_write= fopen("TextFile.txt","w");
if(pf_read==NULL||pf_write==NULL){
printf("%s\n", strerror(errno));
assert(pf_write!=NULL);
assert(pf_read!=NULL);
}
char buffer[100]; //存储从文件读取的二进制码
fgets(buffer, sizeof(buffer),pf_read);//读到文件
int current=2*n-1; //直接指向根结点
int i=0;
while (buffer[i]!='\0'){ //直到当前二进制字符串结束,跳出循环,译码结束
if(buffer[i]=='0'){
current=HT[current].left; //左子树移动,根据之前编码的情况进行选择
} else if(buffer[i]=='1'){
current=HT[current].right; //右子树移动
}
if(HT[current].left==0&&HT[current].right==0){ //孩子结点都为0.说明已经走到叶子结点
fprintf(pf_write, "%c ", HT[current].character);
current=2*n-1; //重置根结点,以便继续解码
}
i++;
}
fclose(pf_read); //关闭文件
fclose(pf_write);
pf_write=NULL; //置为NULL
pf_read=NULL;
} 2.2代码详解
我们先从抽象数据结构类型开始讲解:
我们将哈夫曼树抽象为整形存储结构,对于双亲结点和孩子结点,我们都采用整形存储类型。原因是我们将其用二维数组的存储方式进行存储。对于二维数组的每行的每个元素依次表示这行的权重、双亲结点、左孩子和右孩子。如下:
| HuffmanCode | weight | parent | leftchild | rightchild |
对于HuffmanCode之后会做解释 。
现在解释对于哈夫曼树编码的代码:
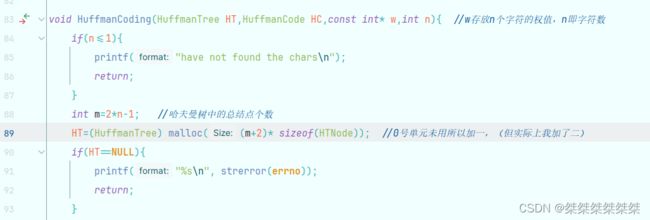
先提前对总结点做计算,通过满二叉树的性质,满二叉树结点的总数等于叶子结点乘二减一,所以我们在对哈夫曼树进行建树前,需要先分配内存空间(注:并非分配2*n-1个结点,我们分配2*n个结点,0号结点我们不使用)(但我在实现代码的时候分配2*n个空间会报栈溢出的问题,所以我分配了2*n+1个结点,当然,欢迎读者尝试),如下图:
然后就是对我们分配的内存空间进行初始化,将每个结点的权值、双亲节点、孩子结点全都赋值为0,然后在将对应权值按顺序分配给不同的结点:
既然权重已经对应分配给各个结点了,那么我们可以开始建树了,先给出我们建树模型,按照下列二维表格表征我们的二维数组哈夫曼树:
| 序号 | weight | parent | leftchild | rightchild |
| 1 | 5 | 9 | 0 | 0 |
| 2 | 29 | 14 | 0 | 0 |
| 3 | 7 | 10 | 0 | 0 |
| 4 | 8 | 10 | 0 | 0 |
| 5 | 14 | 12 | 0 | 0 |
| 6 | 23 | 13 | 0 | 0 |
| 7 | 3 | 9 | 0 | 0 |
| 8 | 11 | 11 | 0 | 0 |
| 9 | 8 | 11 | 1 | 7 |
| 10 | 15 | 12 | 3 | 4 |
| 11 | 19 | 13 | 8 | 9 |
| 12 | 29 | 14 | 5 | 10 |
| 13 | 42 | 15 | 6 | 11 |
| 14 | 58 | 15 | 2 | 12 |
| 15 | 100 | 0 | 13 | 14 |
以及形象的哈夫曼树(哈夫曼树有多种形式,但都是满二叉树):
如上图所示,就是我们建立的哈夫曼树。上图就是通过我们循环找到最小两个结点,然后将最小两个结点的权重相加,生成一个新的结点,新结点的左孩子右孩子结点就为刚刚找到的最小的两个结点:
其中还有一个重要的点就是我们的Selection函数,我们需要通过Selection函数来找到当前所有结点的最小两个值的位置。我们需要将当前的哈夫曼树传入HT、结点数、以及S1与S2的地址。先建立变量用于存储找到的最下位置的值,先将这两个存储变量赋值为-1,然后通过循环来存储对应的位置,a2置于a1前,用来存储前一个的最小值,这样就可以记录下最小的两个值。
至于为什么 i 要从n+1开始循环,因为n以及小于n的数在最开始初始化的时候就已经分配了权值了,所以我们从第n+1个开始,记录我们新生成的结点,以此循环,直到将所有结点都连接起来生成我们的哈夫曼树。但是,注意:因为我们的循环要直到m+1,第十六也要循环,所以会将第15个结点(根节点)的双亲结点也给赋值为 i (16);所以我们需要将其双亲结点赋值为0,因为根节点没有双亲结点:
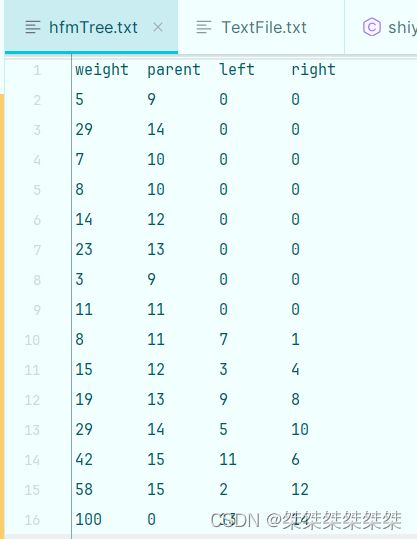
现在将哈夫曼树建立成功之后,我们可以将哈夫曼树写入我们的文件中:
通过写入文件之后,就可以在编码的过程中检查文件中的哈夫曼树判断建树是否成功。
既然建树结束了,那么现在就该到我们的编码步骤了。先解释编码原理:通过将循环,对前n个结点都访问一遍(因为前n个结点为最初的n个结点,编码只需要对最初的编码即可),然后通过循环对结点进行编码:找到当前结点的双亲结点,若双亲结点不为0,则继续进行编译。若当前结点的双亲结点为当前结点的左孩子(简单来说:目前遍历的结点为它双亲结点的左孩子)编码为0,若为右孩子编码为1,直到双亲结点为0(根节点的双亲结点为0)停止这一结点的遍历。
然后将以及编好码的数,存储到文件中(通过简单的循环就可),便于后期可以从文件中读取之后,将其译码:
既然编码的情况已经讲完,那么现在可以到译码的阶段了:
首先需要读取到我们的文件,将刚刚读取的文件中的编码存储到我们的一个数组中,需要从根节点开始寻找叶子结点(一开始用current存储根节点),若当前二进制码为0,则将current赋值为它的左孩子结点,反之,右孩子结点。当当前结点的孩子结点都为0时,表明已经到达叶子结点,将这个结点的权值打印到新的译码文件中。以此循环,直到二进制串译码结束:
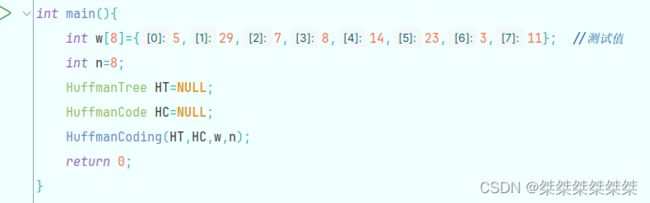
最后给出我们main函数,其中w数组为测试数据:
2.3代码测试
对于哈夫曼树的建立:
对于编码的情况:
对于译码的情况:
由上图所示,我们所测试的情况译码和测试值一样,说明我们的代码可以解决编码译码的问题。
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
分割线
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
欢迎评论区的各位堡子提出意见和指出错误^_^,如果觉得有用就点个赞吧