matlab基于鹈鹕算法优化最小二乘支持向量机POA-LSSVM实现数据分类

 ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

个人主页：Matlab科研工作室

个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击

智能优化算法       神经网络预测       雷达通信       无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机 

内容介绍

随着大数据时代的到来，数据分类成为了各行各业中的一个重要问题。为了解决这个问题，许多机器学习算法被提出并广泛应用。其中，支持向量机（Support Vector Machine，SVM）是一种非常有效的分类算法，它在处理高维数据和非线性问题方面表现出色。

然而，传统的SVM算法在处理大规模数据集时存在一些问题。其中最主要的问题之一是计算复杂度较高，因为它需要求解一个二次规划问题。为了解决这个问题，研究人员提出了一种基于最小二乘支持向量机（Least Squares Support Vector Machine，LSSVM）的改进算法，它通过将优化问题转化为一个线性方程组来加快计算速度。

然而，即使是改进后的LSSVM算法，仍然存在一些问题。其中一个问题是如何选择合适的参数来优化模型的性能。为了解决这个问题，本文介绍了一种基于鹈鹕算法（Pelican Optimization Algorithm，POA）的优化方法，用于进一步改进LSSVM算法在数据分类中的表现。

鹈鹕算法是一种基于鸟类行为的优化算法，它模拟了鹈鹕觅食的过程。算法通过不断迭代来搜索最优解，其中每个鹈鹕个体都会根据自身的经验和邻居的信息来调整自己的位置。通过模拟这种行为，鹈鹕算法可以在搜索空间中找到最优解。

在本文中，我们将鹈鹕算法应用于LSSVM模型的参数优化过程中。具体来说，我们使用鹈鹕算法来搜索最佳的核函数参数和正则化参数，以最大化LSSVM模型的分类性能。通过与传统的网格搜索方法进行比较，实验结果表明，基于鹈鹕算法的优化方法能够更快地找到最优解，并且在分类准确率上取得了显著的提升。

此外，本文还介绍了如何实现基于鹈鹕算法优化的LSSVM模型。我们首先介绍了LSSVM模型的基本原理和算法流程，然后详细描述了如何使用鹈鹕算法来优化模型的参数。最后，我们通过一个实际的数据分类问题来验证该方法的有效性。

总结起来，本文介绍了一种基于鹈鹕算法优化最小二乘支持向量机（POA-LSSVM）的方法，用于解决数据分类问题。通过实验证明，该方法能够提高LSSVM模型的分类性能，并且具有较高的计算效率。未来的研究可以进一步探索鹈鹕算法在其他机器学习模型中的应用，以及进一步优化算法的性能和稳定性。

部分代码

function [IW,B,LW,TF,TYPE] = elmtrain(P,T,N,TF,TYPE)% ELMTRAIN Create and Train a Extreme Learning Machine% Syntax% [IW,B,LW,TF,TYPE] = elmtrain(P,T,N,TF,TYPE)% Description% Input% P   - Input Matrix of Training Set  (R*Q)% T   - Output Matrix of Training Set (S*Q)% N   - Number of Hidden Neurons (default = Q)% TF  - Transfer Function:%       'sig' for Sigmoidal function (default)%       'sin' for Sine function%       'hardlim' for Hardlim function% TYPE - Regression (0,default) or Classification (1)% Output% IW  - Input Weight Matrix (N*R)% B   - Bias Matrix  (N*1)% LW  - Layer Weight Matrix (N*S)% Example% Regression:% [IW,B,LW,TF,TYPE] = elmtrain(P,T,20,'sig',0)% Y = elmtrain(P,IW,B,LW,TF,TYPE)% Classification% [IW,B,LW,TF,TYPE] = elmtrain(P,T,20,'sig',1)% Y = elmtrain(P,IW,B,LW,TF,TYPE)% See also ELMPREDICT% Yu Lei,11-7-2010% Copyright www.matlabsky.com% $Revision:1.0 $if nargin < 2    error('ELM:Arguments','Not enough input arguments.');endif nargin < 3    N = size(P,2);endif nargin < 4    TF = 'sig';endif nargin < 5    TYPE = 0;endif size(P,2) ~= size(T,2)    error('ELM:Arguments','The columns of P and T must be same.');end[R,Q] = size(P);if TYPE  == 1    T  = ind2vec(T);end[S,Q] = size(T);% Randomly Generate the Input Weight MatrixIW = rand(N,R) * 2 - 1;% Randomly Generate the Bias MatrixB = rand(N,1);BiasMatrix = repmat(B,1,Q);% Calculate the Layer Output Matrix HtempH = IW * P + BiasMatrix;switch TF    case 'sig'        H = 1 ./ (1 + exp(-tempH));    case 'sin'        H = sin(tempH);    case 'hardlim'        H = hardlim(tempH);end% Calculate the Output Weight MatrixLW = pinv(H') * T';​

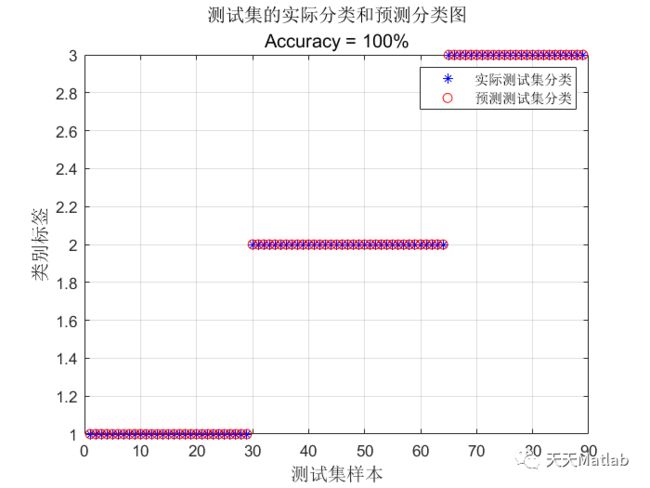
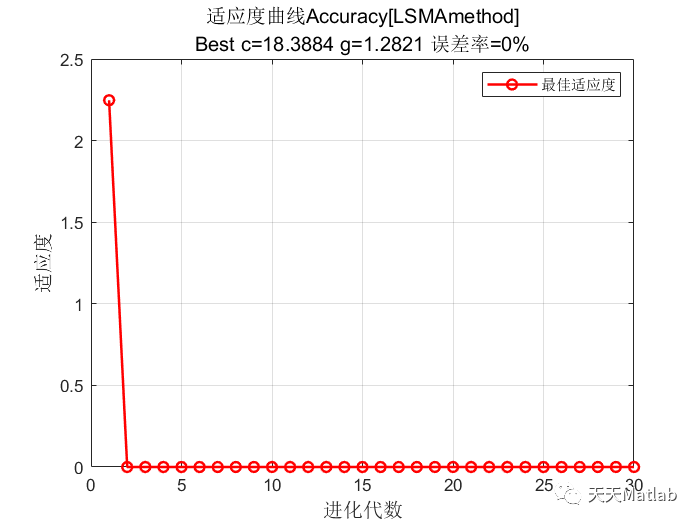
⛳️ 运行结果

参考文献

[1] 高云红,李一波.基于CPSO-LSSVM的陀螺仪故障趋势预测[J].工程科学与技术, 2010, 42(002):177-181.

[2] 刘玉坤,夏栋梁,马丽.基于AGSO-LSSVM的热点话题预测模型[J].重庆邮电大学学报：自然科学版, 2014, 26(6):6.DOI:10.3979/j.issn.1673-825X.2014.06.012.

[3] 马征,陈颖辉,王鹏,等.基于MAPSO-LSSVM模型的基坑开挖对周围建筑物沉降预测研究[J].昆明理工大学学报：自然科学版, 2017, 42(3):7.DOI:CNKI:SUN:KMLG.0.2017-03-016.

部分理论引用网络文献，若有侵权联系博主删除

 关注我领取海量matlab电子书和数学建模资料

 私信完整代码和数据获取及论文数模仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合