代码随想录算法训练营第四十三天|1049. 最后一块石头的重量 II、494. 目标和、474. 一和零

第九章 动态规划part05

1049. 最后一块石头的重量 II

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

• 如果 x == y，那么两块石头都会被完全粉碎；
• 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

拿到还是没什么思路，看了题解。重点是要理解所求最小可能重量即分为两堆石头，重量的最小差值。从而利用动态规划，求出背包总量为所有石头总重量一半时的最大可能重量，再去求差值得到最终结果。

class Solution {
public:
    int lastStoneWeightII(vector& stones) {
        int sum=0;
        for(int i=0;i dp(target+1,0);
        for(int i=stones[0];i<=target;i++){
            dp[i]=stones[0];
        }
        for(int i=1;i0;j--){
                if(j>=stones[i])  dp[j]=max(dp[j],dp[j-stones[i]]+stones[i]);
            }
        }
        return sum-dp[target]-dp[target];
    }
};

494. 目标和

给你一个非负整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

• 例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

还是看了题解，问题转化很巧妙。

本题要如何使表达式结果为target，

既然为target，那么就一定有 left组合 - right组合 = target。

left + right = sum，而sum是固定的。right = sum - left

公式来了， left - (sum - left) = target 推导出 left = (target + sum)/2 。

target是固定的，sum是固定的，left就可以求出来。

此时问题就是在集合nums中找出和为left的组合。

回顾了一下回溯法，虽然超时了

//回溯法（在本题中超时）
class Solution {
public:
    vector> result;
    vector path;
    void backtracking(vector& candidate,int sum,int target,int startIndex){
        if(sum==target){
            result.push_back(path);
        }
        if(sum>target){
            return;
        }
        for(int i=startIndex;i& nums, int target) {
        int sum=0;
        for(int i=0;isum)  return 0;
        if((target+sum)%2)  return 0;
        int left=(sum+target)/2;
        backtracking(nums,0,left,0);
        return result.size();
    }
};

 动态规划：

dp[j]含义：在【0，i】，背包容量（j）刚好填满的方法数；

递推公式：dp[j]+=dp[j-nums[i]];（装满背包递推公式）

初始化：dp[0]=1；

class Solution {
public:
    int findTargetSumWays(vector& nums, int target) {
        int sum=0;
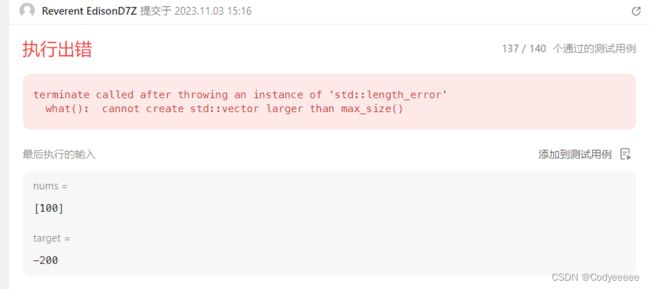
        for(int i=0;isum)  return 0;      //没加abs出现第二个报错
        if((target+sum)%2)  return 0;
        int bagSize=(target+sum)/2;
        vector dp(bagSize+1,0);
        dp[0]=1;
        for(int i=0;i=nums[i];j--){    //如果条件为j>0出现下面第一个报错
                dp[j]+=dp[j-nums[i]];
            }
        }
        return dp[bagSize];
    }
};

474. 一和零

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

这道题看了很久，甚至看了题解一直不能理解，后来发现题意就没读对：应该是子集中所有的字符串的0、1个数总和有限制，求的是最大子集的大小（即子集中最多有多少个字符串）。

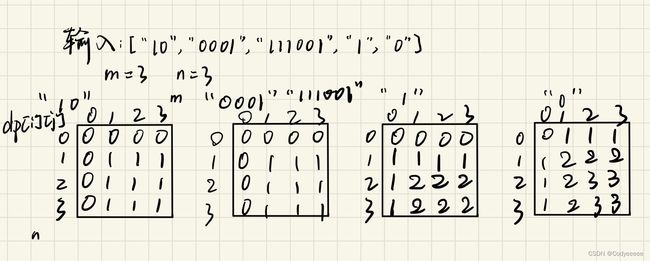
这道题应该是二维背包，dp[i][j]：背包（i个0和j个m）最大子集的长度。

递推公式：dp[i][j]=max(dp[i][j],dp[i-ZeroNum][j-OneNum]+1)；

可以举个例子多推几遍就能理解原理了。 

class Solution {
public:
    int findMaxForm(vector& strs, int m, int n) {
       vector> dp(m+1,vector(n+1,0));
       for(string& str:strs){
           int ZeroNum=0;
           int OneNum=0;
           for(char c:str){
               if(c=='0')  ZeroNum++;
               else OneNum++;
           }
           for(int i=m;i>=ZeroNum;i--){
               for(int j=n;j>=OneNum;j--){
                   dp[i][j]=max(dp[i][j],dp[i-ZeroNum][j-OneNum]+1);
               }
           }
       }
       return dp[m][n]; 
    }
};