Codeforces Round 913 (Div. 3)记录
A题
题意:
一个棋盘,1-8分别表示8行,a-h分别表示8列,比如位置d5表示第5行第4列,给定马棋子原始在的位置,求它能到的位置的编号。
idea:
无脑两个循环输出就行
#include
for(int i=1;i<=8;i++)
{
if( i==r ) continue;
printf("%c%d\n",c,i);
}
for(int i=1;i<=8;i++)
{
char temp = 'a' + i-1;
if( temp == c ) continue;
printf("%c%d\n",temp,r);
}
}
int main()
{
cin>>T;
while(T--)
solve();
return 0;
}
B题
题意:
按给定的顺序输入字符,当时党输入’b’会删除当前最右边的一个小写字母、输入’B’会删除当前最右边的一个大写字母,问最后剩下的字符串是什么。
idea:
一开始想复杂的,每一次删除都用了一次字符串拼接操作,导致T飞了。其实只要从右往左扫描一遍,记忆要删除几个大写、小写字母,把对应位置大小写字符打个标记,最后不出这个位置的字符就行了。
#includeC题
题意:
给一个字符串,每次可以删去两个相邻的不同的字符,问最后能剩下的最短的的字符串的长度。
idea:
我们考虑最后能剩下的字符串会是什么样子的,比如像这样有两种不同的字母:

很明显是不可能的,因为一定可以消除掉其中一个字母的所有字符,所有我们可以知道如果会消不完,最后剩下的一定是只有一种字母的字符串,这种情况只有这种字母的数量大于原字符串的一半长度时才会出现。注意判断一下原字符串长度是不是奇数的情况。
#includeD题
题意:
数轴上,一开始在0位置,有n段区间 [ l i , r i ] , 1 ≤ i ≤ n [ l_i , r_i ],1 \leq i \leq n [li,ri],1≤i≤n,设每一次最大可以移动 k k k的长度,要求移动 i i i步之后落在 [ l i , r i ] [l_i,r_i] [li,ri]这段区间内,问 k k k最小可以是多少。
idea:
一看题就很适合二分,主要是注意check函数里面的一些边界。在check的时候,每走一步都处理一下我可以走到的左边界 l l l和右边界 r r r,再与当前应该处于的区间对比一下,如果与当前应该处于的区间没有重合,就是不行的,不然就更新新的边界继续判断下个区间。
#includeE题
题意:
将 n n n拆分成 n = a + b + c n=a+b+c n=a+b+c的形式,且满足 a , b , c a,b,c a,b,c的数位和之和与 n n n的数位和相等
idea:
我们考虑 n n n正常相加的每一位,比如下面例子中的个位, 3 + 1 + 8 = 12 3+1+8 = 12 3+1+8=12,会发生向前进一位的现象,这种进位对正常加法运算没有影响,但是在算数位和的时候会发现这种进位会导致数值损失了9(减去10加上1),所以题目需要的三元组的每一位单独相加都不应该超过n中这一位的数值。
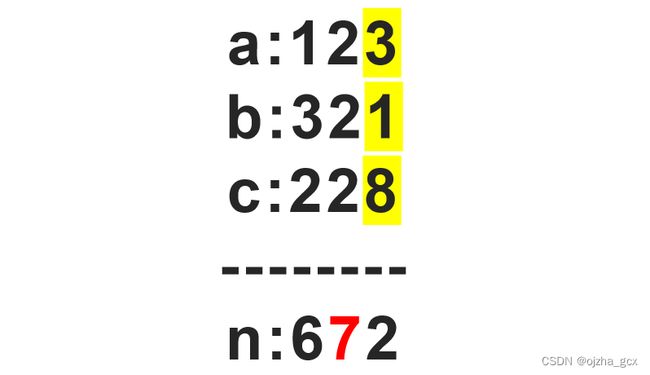
我们可以单独考虑某一位,然后最后将每一位的答案相乘就行。这个时候问题就转变成,某一位的这个数字,能分拆成几种。这里我们考虑隔板法。现在的模型是,有x个一样的小球,用两块隔板分成三份,但是可以为空。我们可以转化成每份至少有一个的模型,有 x + 3 x+3 x+3个一样的小球,用两块隔板分成三份,每份至少有一个小球,先分完每份再减去一个小球就是原模型了。那到这其实答案就跃然纸上了,就是
C x + 3 − 1 2 = C x + 2 2 C_{x+3-1}^{2} = C_{x+2}^{2} Cx+3−12=Cx+22
#include
ans *= a[ tmp ];
}
printf("%lld\n",ans);
}
int main()
{
// #ifndef ONLINE_JUDE
// freopen("in.txt","r",stdin);
// #endif
init();
cin>>T;
while(T--)
solve();
return 0;
}