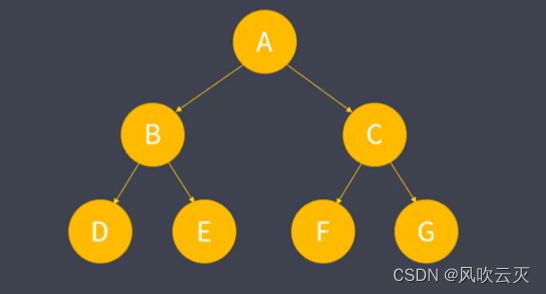
数据结构及其简单实现

栈

1. 先进后出
2. 栈顶操作（栈顶进，栈顶出）

class Strock {
    constructor() {
        this.data = [] // 可以是对象
        this.count = 0
    }
    push(item) {
        // 实现有三种
        // 1. this.data.push(item); 
        // 2. this.data[this.data.length] = item; this.count++
        // 3
        this.data[this.count] = item
        // 入栈后，count 自增
        this.count++
    }
    pop() {
        // 出栈的前提是栈中存在元素，应先行检测
        if (this.isEmpty()) {
            console.log('栈为空！')
            return
        }
        // 移除栈顶数据
        // 方式1：数组方法 pop 移除
        // return this.data.pop()
        // 方式2：计数方式
        const temp = this.data[this.count - 1]
        delete this.data[--this.count]
        return temp
    }
    // isEmpty() 检测栈是否为空
    isEmpty() {
        return this.count === 0
    }
    top() {
        if (this.isEmpty()) {
            console.log('栈为空！')
            return
        }
        return this.data[this.count - 1]
    }
    size() {
        return this.count
    }
    cleatr() {
        this.count = 0
        this.data = []
    }
}

含有min函数的栈

1. 辅助栈实现

// 在存储数据的栈外，再新建一个栈，用于存储最小值
class MinStack {
  constructor () {
    // stackA 用于存储数据
    this.stackA = []
    this.countA = 0
    // stackB 用于将数据降序存储（栈顶值为最小值）
    this.stackB = []
    this.countB = 0
  }
  // 入栈
  push (item) {
    // stackA 正常入栈
    this.stackA[this.countA++] = item
    // stackB 如果没有数据，直接入栈
    // 如果 item 的值 <= stackB 的最小值，入栈
    if (this.countB === 0 || item <= this.min()) {
      this.stackB[this.countB++] = item
    }
  }
  // 最小值函数
  min () {
    return this.stackB[this.countB - 1]
  }
  // 获取栈顶值
  top () {
    return this.stackA[this.countA - 1]
  }
  // 出栈
  pop () {
    // 先进行 stackB 的检测
    // 如果 stackA 的栈顶值 === stackB 的栈顶值，stackB 出栈
    if (this.top() === this.min()) {
      delete this.stackB[--this.countB]
    }
    // stackA 出栈
    delete this.stackA[--this.countA]
  }
}
const m = new MinStack()

2. Math.min方法实现

class MinStack {
  constructor () {
    this.stack = []
  }
  // 入栈
  push (item) {
    this.stack.push(item)
  }
  // 查看栈顶值
  top () {
    return this.stack[this.stack.length - 1]
  }
  // 实现最小值功能
  min () {
    return Math.min.apply(null, this.stack)
  }
  // 出栈方法
  pop () {
    return this.stack.pop()
  }
}
const m = new MinStack()

每日温度

力扣题目 739. 每日温度

function s(arr) {
    let data = [0] // data是一个逆序栈 （变-> 小） 存储入栈的下标
    let count = 1
    let returnArr = Array(arr.length).fill(0)
    for (let index = 1; index < arr.length; index++) {
        const element = arr[index];
        while (count && element > arr[data[count - 1]]) {
            let i = data.pop()
            count--
            returnArr[i] = index - i
        }
        data.push(index)
        count++
    }
    return returnArr
}
console.log(s([73, 74, 75, 71, 69, 72, 76, 73])) // [1, 1, 4, 2, 1, 1, 0, 0]

队列

1. 先进先出
2. 队首出，队尾入

class Queue {
  constructor () {
    // 用于存储队列数据
    this.queue = []
    this.count = 0
  }
  // 入队方法
  enQueue (item) {
    this.queue[this.count++] = item
  }
  // 出队方法
  deQueue () {
    if (this.isEmpty()) {
      return
    }
    // 删除 queue 的第一个元素
    // delete this.queue[0]
    // 利用 shift() 移除数组的第一个元素
    this.count--
    return this.queue.shift()
  }
  isEmpty () {
    return this.count === 0
  }
  // 获取队首元素值
  top () {
    if (this.isEmpty()) {
      return
    }
    return this.queue[0]
  }
  size () {
    return this.count
  }
  clear () {
    // this.queue = []
    this.length = 0
    this.count = 0
  }
}
const q = new Queue()

基于对象

class Queue {
  constructor () {
    this.queue = {}
    this.count = 0
    // 用于记录队首的键
    this.head = 0
  }
  // 入队方法
  enQueue (item) {
    this.queue[this.count++] = item
  }
  // 出队方法
  deQueue () {
    if (this.isEmpty()) {
      return
    }
    const headData = this.queue[this.head]
    delete this.queue[this.head]
    this.head++
    return headData
  }
  length () {
    return this.count - this.head
  }
  top () {
  	return this.queue(this.head)
  }
  isEmpty () {
    return this.length() === 0
  }
  clear () {
    this.queue = {}
    this.count = 0
    this.head = 0
  }
}
const q = new Queue()

双端队列

class Deque {
  constructor () {
    this.queue = {}
    this.count = 0
    this.head = 0
  }
  // 队首添加
  addFront (item) {
    this.queue[--this.head] = item
  }
  // 队尾添加
  addBack (item) {
    this.queue[this.count++] = item
  }
  // 队首删除
  removeFront () {
    if (this.isEmpty()) {
      return
    }
    const headData = this.queue[this.head]
    delete this.queue[this.head++]
    return headData
  }
  // 队尾删除
  removeBack () {
    if (this.isEmpty()) {
      return
    }
    const backData = this.queue[this.count - 1]
    delete this.queue[--this.count]
    // this.count-- 与 上一步 this.count - 1 合并
    return backData
  }
  // 获取队首值
  frontTop () {
    if (this.isEmpty()) {
      return
    }
    return this.queue[this.head]
  }
  // 获取队尾值
  backTop () {
    if (this.isEmpty()) {
      return
    }
    return this.queue[this.count - 1]
  }
  isEmpty () {
    return this.size() === 0
  }
  size () {
    return this.count - this.head
  }
}
const deq = new Deque()

队列的最大值

var MaxQueue = function() {
  // 存储队列数据
  this.queue = {}
  // 双端队列维护最大值（每个阶段的最大值）
  this.deque = {}
  // 准备队列相关的数据
  this.countQ = this.countD = this.headQ = this.headD = 0
};

/** 队尾入队
 * @param {number} value
 * @return {void}
 */
MaxQueue.prototype.push_back = function(value) {
  // 数据在 queue 入队
  this.queue[this.countQ++] = value
  // 检测是否可以将数据添加到双端队列
  //   - 队列不能为空
  //   - value 大于队尾值
  while (!this.isEmptyDeque() && value > this.deque[this.countD - 1]) {
    // 删除当前队尾值
    delete this.deque[--this.countD]
  }
  // 将 value 入队
  this.deque[this.countD++] = value
};

/** 队首出队
 * @return {number}
 */
MaxQueue.prototype.pop_front = function() {
  if (this.isEmptyQueue()) {
    return - 1
  }
   // 给 queue 出队，并返回
  const frontData = this.queue[this.headQ]
  // 比较 deque 与 queue 的队首值，如果相同，deque 出队，否则 deque 不操作
  if (frontData  === this.deque[this.headD]) {
    delete this.deque[this.headD++]
  }
  delete this.queue[this.headQ++]
  return frontData
};

/** 获取队列最大值
 * @return {number}
 */
MaxQueue.prototype.max_value = function() {
  if (this.isEmptyDeque()) {
    return -1
  }
  // 返回 deque 队首值即可
  return this.deque[this.headD]
};

/** 检测队列 deque 是否为空
 * 
 */
MaxQueue.prototype.isEmptyDeque = function () {
  return !(this.countD - this.headD)
};

/** 检测队列 Queue 是否为空
 * 
 */
MaxQueue.prototype.isEmptyQueue = function () {
  return !(this.countQ - this.headQ)
};

滑动窗口问题

力扣题目 239. 滑动窗口最大值

/**
 * @param {number[]} nums 传入数组
 * @param {number} k 滑动窗口宽度
 * @return {number[]} 
 */
var maxSlidingWindow = function(nums, k) {
  if (k <= 1) {
    return nums
  }
  const result = []
  const deque = []
  // 1 将窗口第一个位置的数据添加到 deque 中，保持递减
  deque.push(nums[0])
  let i = 1
  for (; i < k; i++) {
    // - 存在数据
    // - 当前数据大于队尾值
    //   - 出队，再重复比较
    while (deque.length && nums[i] > deque[deque.length - 1]) {
      deque.pop()
    }
    deque.push(nums[i])
  }
  // 将第一个位置的最大值添加到 result
  result.push(deque[0])
  // 2 遍历后续的数据
  const len = nums.length
  for (; i < len; i++) {
    // 同上进行比较
    while (deque.length && nums[i] > deque[deque.length - 1]) {
      deque.pop()
    }
    deque.push(nums[i])
    // 检测当前最大值是否位于窗口外
    if (deque[0] === nums[i - k]) {
      deque.shift()
    }
    // 添加最大值到 result
    result.push(deque[0])
  }
  return result
};

链表

操作上和数组很像，为什么不用数组？

• 数组添加、移除会导致后续元素位移，性能开销大。
• 获取、修改元素时，数组效率高
• 添加、删除元素时，链表效率高

链表实现

• 节点类： value、next
• 链表类
  – addAtTail 尾部添加节点
  – addHead 头部添加节点
  – addAtIndex 指定位置添加节点
  – get 获取节点
  – removeAtIndex 删除指定节点
  – size 节点个数

// 节点类
class LinkedNode {
  constructor (value) {
    this.value = value
    // 用于存储下一个节点的引用
    this.next = null
  }
}

// 链表类
class LinkedList {
  constructor () {
    this.count = 0
    this.head = null
  }
  // 添加节点 (尾）
  addAtTail (value) {
    // 创建新节点
    const node = new LinkedNode(value)
    // 检测链表是否存在数据
    if (this.count === 0) {
      this.head = node
    } else {
      // 找到链表尾部节点，将最后一个节点的 next 设置为 node
      let cur = this.head
      while (cur.next != null) {
        cur = cur.next
      }
      cur.next = node
    }
    this.count++
  }
  // 添加节点（首）
  addAtHead (value) {
    const node = new LinkedNode(value)
    if (this.count === 0) {
      this.head = node
    } else {
      // 将 node 添加到 head 的前面
      node.next = this.head
      this.head = node
    }
    this.count++
  }
  // 获取节点（根据索引）
  get (index) {
    if (this.count === 0 || index < 0 || index >= this.count) {
      return
    }
    // 迭代链表，找到对应节点
    let current = this.head
    for (let i = 0; i < index; i++) {
      current = current.next
    }
    return current
  }
  // 添加节点（根据索引）
  addAtIndex (value, index) {
    if (this.count === 0 || index >= this.count) {
      return
    }
    // 如果 index <= 0，都添加到头部即可
    if (index <= 0) {
      return this.addAtHead(value)
    }
    // 后面为正常区间处理
    const prev = this.get(index - 1)
    const next = prev.next

    const node = new LinkedNode(value)
    prev.next = node
    node.next = next

    this.count++
  }
  // 删除（根据索引）
  removeAtIndex (index) {
    if (this.count === 0 || index < 0 || index >= this.count) {
      return
    }
    if (index === 0) {
      this.head = this.head.next
    } else {
      const prev = this.get(index - 1)
      prev.next = prev.next.next
    }
    this.count--
  }
}

链表的形式

1. 双向链表
2. 循环链表
   力扣题目 024. 反转链表

• 循环实现

var reverseList = function(head) {
  // 声明变量记录 prev、cur
  let prev = null
  let cur = head
  // 当 cur 是节点时，进行迭代
  while (cur) {
    // 先保存当前节点的下一个节点
    const next = cur.next
    cur.next = prev
    prev = cur
    cur = next
  }
  return prev
};

• 递归实现

var reverseList = function(head) {
  if (head === null || head.next === null) {
    return head
  }
  const newHead = reverseList(head.next)
  // 能够第一次执行这里的节点为 倒数第二个 节点
  head.next.next = head
  // head 的 next 需要在下一次递归执行时设置。当前设置为 null 不影响
  //   - 可以让最后一次（1）的 next 设置为 null
  head.next = null
  return newHead
};

力扣题目 022. 环形链表 II

var detectCycle = function(head) {
    if (head === null || head.next === null) {
      return null
    }
    // 声明快慢指针
    let slow = head
    let fast = head

    while (fast !== null) {
      // 慢每次指针移动一位
      slow = slow.next
      // 如果满足条件，说明 fast 为尾部结点，不存在环
      if (fast.next === null) {
        return null
      }
      // 快指针每次移动两位
      fast = fast.next.next

      // 检测是否有环
      if (fast === slow) {
        // 找到环的起点位置
        let ptr = head
        while (ptr !== slow) {
          ptr = ptr.next
          slow = slow.next
        }
        // ptr 和 slow 的交点就是环的起始节点
        return ptr
      }
    }
    // while 结束，说明 fast 为 null，说明链表没有环
    return null
};

树

1. 满二叉树 （每个节点都有左右子节点）
   
2. 完全二叉树

• 最低层的节点在最左侧
• 上面的层级都是满二叉树
  

二叉树遍历

1. 前序遍历
   根结点 -> 左子树 -> 右子树
   上图顺序为 ABDHIECFG
2. 中序遍历
   左子树 -> 根结点 -> 右子树
   
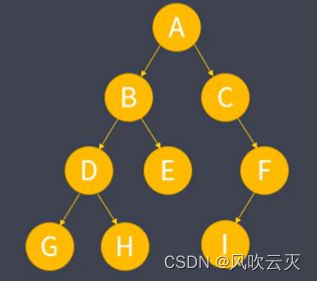
   上图遍历顺序： GDHBEACIF
3. 后序遍历
   左子树 -> 右子树 -> 根结点
   上图遍历顺序： GHDEBIFCA

前序、中序、后序都是深度优先遍历

力扣题目 二叉树的前序遍历

• 递归实现

var preorderTraversal = function(root) {
  // 用于存储遍历的结果
  const res = []
  // 设置函数用于进行递归遍历
  const preorder = (root) => {
    // 当前结点为空时，无需进行递归
    if (!root) {
      return
    }
    // 记录根节点值
    res.push(root.val)
    // 前序遍历左子树
    preorder(root.left)
    // 前序遍历右子树
    preorder(root.right)
  }
  preorder(root)
  return res
}; 

• 迭代 实现

const preorderTraversal = function(root) {
  const res = []
  const stk = [] // 栈
  while (root || stk.length) {
    while (root) {
      // 右子结点入栈
      stk.push(root.right)
      // 记录根节点
      res.push(root.val)
      // 下一步处理左子节点
      root = root.left
    }
    // 左子树处理完毕，将 stk 出栈，处理右子树
    root = stk.pop()
  }
  return res
}

力扣题目 104. 二叉树的最大深度

var maxDepth = function(root) {
  if (!root) {
    return 0
  }
  return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1
};

广度优先

即是逐层遍历

var levelOrder = function(root) {
  const res = []
  if (!root) {
      return res
  }
  // 声明队列用于存储后续数据
  const q = []
  q.push(root)

  // 遍历队列
  while (q.length !== 0) {
      // 针对本轮操作，创建一个新的二维数组
      res.push([])
      let len = q.length
      for (let i = 0; i < len; i++) {
          // 将本次操作的结点出队
          const node = q.shift()
          res[res.length - 1].push(node.val)
          // 检测是否存在左右子结点，如果有，入队即可
          if (node.left) {
              q.push(node.left)
          }
          if (node.right) {
              q.push(node.right)
          }
      }
  }
  return res
};

二叉搜索树

左子树小于根结点，右子树大于根结点
力扣题目 98. 验证二叉搜索树

 var isValidBST = function(root) {
  // 通过一个辅助函数来统一设置左右子树的比较
  return helper(root, -Infinity, Infinity);
};

const helper = (root, lower, upper) => {
  if (root === null) {
    return true
  }
	// 当前节点值超出边界，说明二叉树为非 BST
  if (root.val <= lower || root.val >= upper) {
    return false;
  }
  // 否则，递归处理左右子节点，并更新大小范围
  // 同时根据左右子节点的返回值进行返回，只有全部递归结果均为 true， 才说明二叉树为 BST
  return helper(root.left, lower, root.val) && helper(root.right, root.val, upper);
} 

中序遍历迭代实现

function ss(root) {
    let res = []
    let dep = []
    while (root || dep.length) {
        while (root) {
            dep.push(root)
            root = root.left
        }
        root = dep.pop()
        res.push(root.val)
        root = root.right
    }
    return res
}

中序遍历验证二叉搜索树
原理是中序遍历后的数组是一个从小到大的数组， 只需要将当前的值和上一项的值做比较。

var isValidBST = function(root) {
  let stk = []
  // 用于记录上一次取得的节点值，BST 中这个值应小于当前节点
  // 设置默认值为 -Infinity 避免对比较结果产生干扰
  let oldNode = -Infinity

  while (root || stk.length) {
    while (root) {
      stk.push(root) 
      root = root.left
    }
    root = stk.pop()
    // 如果任意节点比上个节点值小，说明二叉树不是 BST
    if (root.val <= oldNode) {
      return false
    }
    // 通过比较，记录当前节点值
    oldNode = root.val
    root = root.right
  }
  return true
};