RPC之对象序列化/反序列化

从传统的单体服务到现在的分布式服务，微服务截然已经成为主流。RPC作为微服务最重要的核心模块之一，也越来越受到关注。市场主流的rpc有dubbo、spring cloud、thrift、grpc、brpc等。

 

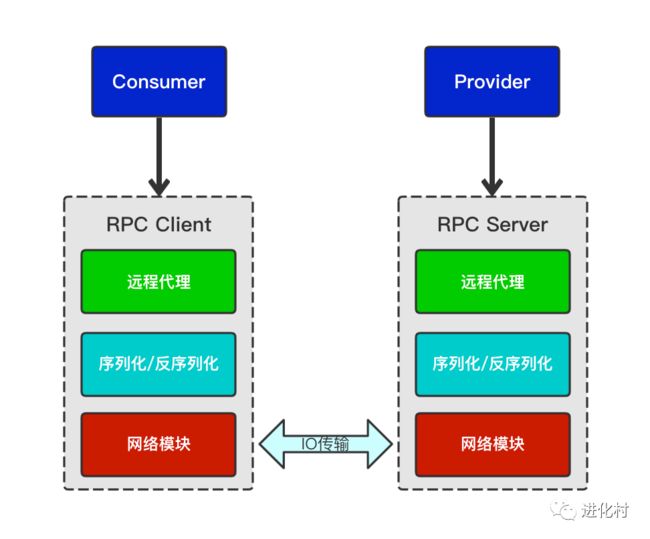
那RPC的通信传输数据方式是什么样子呢？我们通过下面一张图来看下

服务调用方（consumer）将数据序列化打包通过网络模块传给服务提供方（provider）。provider将接收到的数据包反序列化，得到相应的参数数据。然后根据参数从DB查询出业务数据，然后将数据序列化返给调用方。调用方再将数据包反序列化，最终得到想要的数据。

 

这就是一次简单的RPC通信，聊到这还感觉不到什么，但细品下发现没那么简单。网络模块是通过二进制流的方式进行传输的，RPC发送的数据对象是怎么转换成二进制的？

 

有同学说，通过调用工具类将对象序列化成字节流喽。这么说是没毛病的，但仔细想想，对象中可能会包含：8种基本数据类型(整型：byte，short，int，long 浮点型：float，double 字符型：char 布尔型：boolean)、引用数据类型（类、数组）。引用数据类型中又由基本数据类型组成，这么分析下来，就落到底层的序列化单元：基本类型。

 

那么问题来了，基本数据类型是怎么转成字节数组的？先补充两个词汇的基本概念：

bit（位）：位是计算机中存储数据的最小单位，指二进制数中的一个位数，其值为“0”或“1”。

byte（字节）：字节是计算机存储容量的基本单位，一个字节由8位二进制数组成。

 

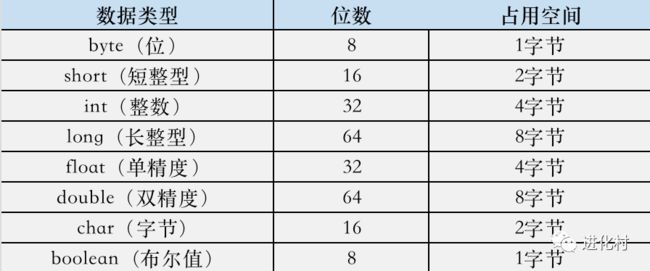
关于Java的8种基本数据类型，其名称、位数、占用空间如下表所示：

 

 

计算机为什么采用二进制

计算机中我们经常使用的进制主要有：二进制、八进制、十进制、十六进制。为什么计算机选用二进制数制，其他进制不香吗？

 

ALU数字逻辑单元(ArithmeticLogicUnit)，亦称算术逻辑部件，是处理器中的一个功能模块。用来执行诸如加减乘除以及寄存器中的值之间的逻辑运算。数制操作运算器能执行多少种操作和操作速度，标志着运算器能力的强弱，甚至标志着计算机本身的能力。而二进制是在物理上最容易实现的，因为只有高、低两个电平表示1和0。二进制数用来表示的二进制数的编码、计数、加减运算规则简单。

 

计算机为什么要用补码

对于一个数，计算机要使用一定编码方式存储。补码是计算机存储一个具体数字的编码方式。在探求为何计算机要使用补码之前，我们先了解下原码、反码、补码的概念。

 

数分正数和负数，所以机器数是带符号的。在计算机中用一个数的高位存放符号，正数为0，负数为1。比如2，以字长为8位，转成二进制就是[00000010],-2就是[10000010]，负数最高符号位是1。

 

原码：原码就是符号位加上真值的绝对值。2=[00000010]、-2=[10000010]

反码：正数的反码是其本身；负数的反码是在原码的基础上，符号位不变，其余各位取反。2反码=[00000010]、-2反码=[11111101]

补码：正数的补码就是其本身；负数的补码是在其原码的基础上， 符号位不变,，其余各位取反。即反码+1。2补码=[00000010]、-2补码=[11111110]

 

我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 ，所以机器可以只有加法而没有减法，这样计算机运算的设计就更简单了。

 

于是人们开始探索，将符号位参与运算, 并且只保留加法的方法. 

 

首先来看原码：计算十进制的表达式: 1-1=0

1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2

 

如果用原码表示，让符号位也参与计算，显然对于减法来说，结果是不正确的。这也就是为何计算机内部不使用原码表示一个数。为了解决原码做减法的问题, 出现了反码:

1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0

 

发现用反码计算减法，结果的真值部分是正确的. 但又出现了新的问题，其实就出现在"0"这个特殊的数值上。虽然人们理解上+0和-0是一样的，但是0带符号是没有任何意义的. 而且会有[0000 0000]原和[1000 0000]原两个编码表示0.

 

于是补码的出现, 解决了0的符号以及两个编码的问题：1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补 = [0000 0000]原

这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了。

 

位移运算

了解了计算机采用补码的编码方式存储，要获取一个数的补码，首先要通过二进制计算出原码和反码，然后反码+1才得出补码。这些计算都是计算机在系统底层完成的，我们不需要计算。我们要做的就是把要存储的数字正确给到程序就可以。字节是计算机存储容量的基本单位，一个字节由8位二进制数组成。int类型是4个字节，32位。byte类型1个字节，8位。那int类型是怎么转byte数组呐？

 

int是32位，byte是8位，如果要转换成byte的需要4个byte才能容得下。我们来分析下思路，8的二进制是[00000000 00000000 00000000 00001000]，转成byte数组[00000000][00000000][00000000][00001000]，相等于把int类型的二进制截成了4(32/8)段，每段放了8个二进制数。但在程序上该怎么处理来完成这个截取动作？对，就是位移运算。

<< : 左移运算符，将运算符左边的对象向左移动运算符右边指定的位数（在低位补0）
>>："有符号"右移运算 符，将运算符左边的对象向右移动运算符右边指定的位数。使用符号扩展机制，如果值为正，则在高位补0，如果值为负，则在高位补1.
>>>："无符号"右移运算 符，将运算符左边的对象向右移动运算符右边指定的位数。采用0扩展机制，无论值的正负，都在高位补0

 

0XFF

位移运算符实现了对二进制数据的高低位移动，也就是int的4段8位的二进制数可以通过位移8位、16位、24位，像指针一样移动到任意一段上。但只是位移还不够，没有完成截取操作。所以下一步我们还要完成截取的操作。先来看段源码

public static byte[] intToBytes(int i) {      byte[] targets = new byte[4];      targets[3] = (byte) (i & 0xFF);      targets[2] = (byte) (i >> 8 & 0xFF);      targets[1] = (byte) (i >> 16 & 0xFF);      targets[0] = (byte) (i >> 24 & 0xFF);      return targets;  }

这段代码逻辑就是将int以每8位为一段，截取后放到byte数组中。&0xFF是什么鬼？

 

0x代表16进制数，0xFF对应的十进制数是255，二进制是[11111111]。和其进行&操作的数，最低8位不会发生变化，也就是byte &0xFF只是对其最低8位的复制。这样的话通过位移和&0xFF运算，就能很巧妙的截取不同段位的8个字节数。

 

&表示按位与，只有两个位同时为1，才能得到1。|表示按位或，有一个为1，其值就是1。

 

byte数组又是如何还原成int，大体思路就是将原来截取的4段8位的二进制数，通过或运算按先后顺序拼接起来。看源码​​​​​​​

public static int bytesToInt(byte[] bytes, int off) {      int b0 = bytes[off] & 0xFF;      int b1 = bytes[off + 1] & 0xFF;      int b2 = bytes[off + 2] & 0xFF;      int b3 = bytes[off + 3] & 0xFF;      return (b0 << 24) | (b1 << 16) | (b2 << 8) | b3;  }

上面的两个操作过程，完成了int到byte数组的互相转化。在序列化一个对象的时候，需要遍历对象的数据成员，根据数据成员的类型来获得各自的字节长度进行转化。但在实际的RPC通信中，会远比这个流程复杂。需要处理的不单单是基本数据类型还有集合、数组、枚举等引用类型。

 

了解底层实现原理，可以帮助我们理清思路，知道各个环节做了什么事情。当出现问题时，我们也能按图索骥找到解决方案。

 

总结

RPC通信，通过序列化/反序列化方式处理数据。序列化，是循环获取对象中基本数据类型转成byte数组或者其他形式数据。反序列化，是根据描述将byte数据或者其他形式数据转化为原来的基本数据类型并赋值。在转化的过程中用到了”位移“和“与或“运算。

 

成长篇

        OKR工作法

        金字塔工作法

        富兰克林

技术篇

       从0开始学架构

       重新定义SpringCloud

       如何快速掌握Go语言

 

                                                   扫描二维码关注公众号，一起持续进化