【链表】系列题目精选(1)
理论
具体参考 链接1,链接2
像带环链表 或一个连续数组里面只有一个数重复,找环。除了常见的哈希表,都可以用快慢指针来做:
- 第一次遍历1:2的速度,若相遇只能证明有环,相遇位置有可能在环内任一位置;
- 若要找到环的入口,必须将slow重置至到表头,两指针按相同速度重新走,再次相遇的地方即为环的入口;(为什么1:2速度走第一次相遇后时,slow要充值到表头再走必相遇环入口。可证明,见解答)
常用方法待整理
例题
涉及到链表的操作,一定要在纸上把过程先画出来,再写程序。
leetcode206. 反转链表
反转一个单链表。 示例:
- 输入: 1->2->3->4->5->NULL
- 输出: 5->4->3->2->1->NULL
思路
好理解的双指针
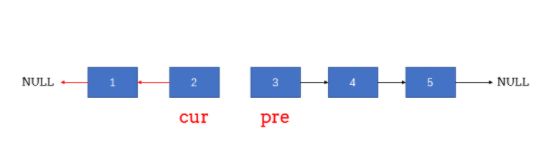
- 定义两个指针: pre 和 cur ;pre 在前 cur 在后。
- 每次让 pre 的 next 指向 cur ,实现一次局部反转
- 局部反转完成之后,pre 和 cur 同时往前移动一个位置
- 循环上述过程,直至 prepre 到达链表尾部
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode *left = NULL, *right = head;
while(right != NULL){
ListNode *t = right->next;
right->next = left;
left = right;
right = t;
}
return left;
}
};
其他解法详解 解答
leetcode92. 反转链表 II
上一题全反转,此题是根据指定区间部分反转
给你单链表的头节点 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
思路
法1.反转中间部分,再调整两端指针
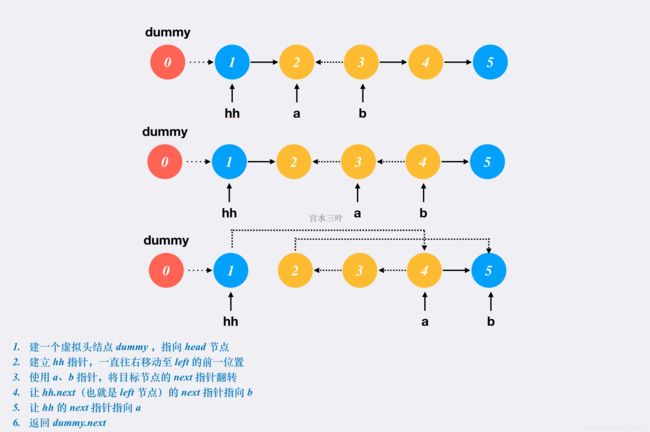
为了减少边界判断,我们可以建立一个虚拟头结点 dummy,使其指向 head,最终返回 dummy.next。
这种「哨兵」技巧能应用在所有的「链表」题目。
黄色部分的节点代表需要「翻转」的部分:
思路同上题,反转中间部分,最后再调整两端指针
之后就是常规的模拟,步骤写在示意图里啦 ~
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int l, int r) {
ListNode* dummyHead = new ListNode(0);
dummyHead->next = head;
// 注意这里是 L 不是 1
r -= l;
// hh 就是 “哈哈” 的意思 ...
// 啊呸。hh 是 head 的意思,为了防止与 height 的简写 h 冲突
ListNode* hh = dummyHead;
while (l-- > 1)
hh = hh->next;
ListNode* prv = hh->next;
ListNode* cur = prv->next;
while (r-- > 0) {
ListNode* nxt = cur->next;
cur->next = prv;
prv = cur;
cur = nxt;
}
hh->next->next = cur;
hh->next = prv;
return dummyHead->next;
}
};
法2.头插法(一次遍历「穿针引线」反转链表)
整体思想是:在需要反转的区间里,每遍历到一个节点,让这个新节点来到反转部分的起始位置。下面的图展示了整个流程。
下面我们具体解释如何实现。使用三个指针变量 pre、curr、next 来记录反转的过程中需要的变量,它们的意义如下:
- curr:指向待反转区域的第一个节点 left;
- next:永远指向 curr 的下一个节点,循环过程中,curr 变化以后 next 会变化;
- pre:永远指向待反转区域的第一个节点 left 的前一个节点,在循环过程中不变。
具体详细解释参见 官方解答
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int left, int right) {
ListNode *dummy = new ListNode(-1), *pre = dummy;
dummy->next = head;
//移动到left左边一个节点
for(int i = 0; i < left - 1; i++) pre = pre->next;
ListNode * cur = pre->next;
//头插法:pre不变,一直在left左边,cur和nxt一直向后移动
for(int i = 0; i < right - left; i++){
ListNode *nxt = cur->next;
cur->next = nxt->next;
nxt->next = pre->next;
pre->next = nxt;
}
return dummy->next;
}
};
leetcode83. 删除排序链表中的重复元素
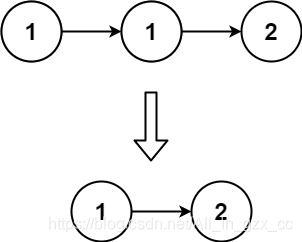
存在一个按升序排列的链表,给你这个链表的头节点 head ,请你删除所有重复的元素,使每个元素 只出现一次 。
返回同样按升序排列的结果链表。
思路分析
链表删除一个节点时,需要将指针指到其前面一个位置。
由于给定的链表是排好序的,因此重复的元素在链表中出现的位置是连续的,因此我们只需要对链表进行一次遍历,就可以删除重复的元素。
- 具体地:
- 我们从指针 cur 指向链表的头节点,随后开始对链表进行遍历。
- 如果当前 cur 与 cur.next 对应的元素相同,那么我们就将 cur.next 从链表中移除;否则说明链表中已经不存在其它与 cur 对应的元素相同的节点,因此可以将 cur 指向 cur.next。
- 当遍历完整个链表之后,我们返回链表的头节点即可。
细节
当我们遍历到链表的最后一个节点时,cur.next 为空节点,如果不加以判断,访问 cur.next 对应的元素会产生运行错误。因此我们只需要遍历到链表的最后一个节点,而不需要遍历完整个链表。注意下面 C++ 代码中并没有释放被删除的链表节点的空间。如果在面试中遇到本题,读者需要针对这一细节与面试官进行沟通。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
ListNode *p = head;
if(head == NULL || head->next == NULL) return head;
while(p->next){
if(p->val == p->next->val){
p->next = p->next->next;//保存前一个,不后移p指针,因为还要和后面一个值继续比
}else{
p = p->next;//只有两个值不同才更新下一个节点
}
}
return head;
}
};
leetcode82. 删除排序链表中的重复元素 II
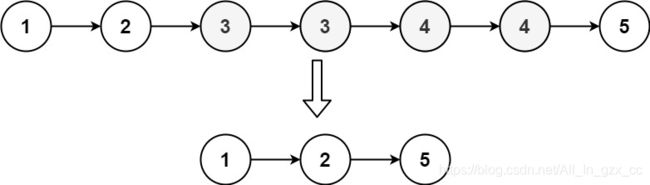
存在一个按升序排列的链表,给你这个链表的头节点 head ,请你删除链表中所有存在数字重复情况的节点,只保留原始链表中 没有重复出现
的数字。 返回同样按升序排列的结果链表。
思路分析
对比上题,此题是所有重复元素都要删除。而链表删除一个节点时,需要将指针指到其前面一个位置。
由于给定的链表是排好序的,因此重复的元素在链表中出现的位置是连续的,因此我们只需要对链表进行一次遍历,就可以删除重复的元素。由于链表的头节点可能会被删除,因此我们需要额外使用一个哑节点(dummynode)指向链表的头节点。
- 具体地:
- 我们从指针cur 指向链表的哑节点,随后开始对链表进行遍历。
- 如果当前 cur.next 与cur.next.next 对应的元素相同,那么我们就需要将cur.next 以及所有后面拥有相同元素值的链表节点全部删除。
2.1 我们记下这个元素值 x,随后不断将 cur.next 从链表中移除,直到 cur.next 为 空节点 或者 其元素值不等于 x 为止。此时,我们将链表中所有元素值为 x 的节点全部删除。- 如果当前 cur.next 与 cur.next.next 对应的元素不相同,那么说明链表中只有一个元素值为 cur.next的节点,那么我们就可以将 cur 指向 cur.next。
- 当遍历完整个链表之后,我们返回链表的的哑节点的下一个节点 dummy.next 即可。
细节
需要注意 cur.next 以及 cur.next.next 可能为空节点,如果不加以判断,可能会产生运行错误。注意下面 C++代码中并没有释放被删除的链表节点以及哑节点的空间。如果在面试中遇到本题,读者需要针对这一细节与面试官进行沟通。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
if(head == nullptr || head->next == nullptr) return head;
//指针必须指到要删除节点的前一个节点,所以此处要在开头添加一个哨兵节点
ListNode *dummy = new ListNode(0, head);
ListNode *cur = dummy;
while(cur->next && cur->next->next){//要删除的节点必须存在
if(cur->next->val == cur->next->next->val){//存在两个节点值相等
int x = cur->next->val;
while(cur->next && cur->next->val == x){
cur->next = cur->next->next;//递归比较,把哨兵节点指向后一个
}
}else{
cur = cur->next;
}
}
return dummy->next;
}
};
leetcode257. 二叉树的所有路径
给定一个二叉树,返回所有从根节点到叶子节点的路径。 说明: 叶子节点是指没有子节点的节点。
输入:
1
/ \
2 3
\
5
输出: [“1->2->5”, “1->3”]
思路分析
正常的回溯思路,但要注意为啥没有显式的撤销操作:
因为此处子路径path是值传递,没传递地址,所以每次都用都copy一份,不影响上一个递归里的path内容, 所以后面不必显式的回溯撤销
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void dfs(vector<string>& ans, TreeNode* p, string path){
//终止条件
if(p == nullptr) return;
path += to_string(p->val);
if(p->left == nullptr && p->right == nullptr){
ans.push_back(path);
return;
}
//此处子路径path是值传递,没传递地址,所以每次都用都copy一份,不影响上一个递归里的path内容,所以后面不必显式的回溯撤销
path += "->";
dfs(ans, p->left, path);
dfs(ans, p->right, path);
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> ans;
dfs(ans, root, "");
return ans;
}
};
leetcode141. 环形链表
给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos
来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意:pos
不作为参数进行传递,仅仅是为了标识链表的实际情况。 如果链表中存在环,则返回 true 。 否则,返回 false 。 进阶: 你能用
O(1)(即,常量)内存解决此问题吗?
思路分析
- 哈希表
最容易想到的方法是遍历所有节点,每次遍历到一个节点时,判断该节点此前是否被访问过。
具体地,我们可以使用哈希表来存储所有已经访问过的节点。每次我们到达一个节点,如果该节点已经存在于哈希表中,则说明该链表是环形链表,否则就将该节点加入哈希表中。重复这一过程,直到我们遍历完整个链表即可。
class Solution {
public:
bool hasCycle(ListNode *head) {
unordered_set<ListNode*> seen;
while (head != nullptr) {
if (seen.count(head)) {
return true;
}
seen.insert(head);
head = head->next;
}
return false;
}
};
- 快慢指针
一快一慢,有环必定相遇!类比小学时做的环形跑道数学题。
为什么我们要规定初始时慢指针在位置 head,快指针在位置 head.next,而不是两个指针都在位置
head(即与「乌龟」和「兔子」中的叙述相同)?观察下面的代码,我们使用的是 while 循环,循环条件先于循环体。由于循环条件一定是判断快慢指针是否重合,如果我们将两个指针初始都置于
head,那么 while 循环就不会执行。因此,我们可以假想一个在 head 之前的虚拟节点,慢指针从虚拟节点移动一步到达
head,快指针从虚拟节点移动两步到达 head.next,这样我们就可以使用 while 循环了。当然,我们也可以使用 do-while 循环。此时,我们就可以把快慢指针的初始值都置为 head。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
//快慢指针:只要相遇就有环
bool hasCycle(ListNode *head) {
if(head == NULL || head->next == NULL) return false;
ListNode *slow = head, *fast = head;
do{
slow = slow->next;
fast = fast->next->next;
if(fast == NULL || fast->next == NULL)
return false;
}while(slow != fast);
return true;
}
};
//============================另一种写法=================================
class Solution {
public:
bool hasCycle(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return false;
}
ListNode* slow = head;
ListNode* fast = head->next;
while (slow != fast) {
if (fast == nullptr || fast->next == nullptr) {
return false;
}
slow = slow->next;
fast = fast->next->next;
}
return true;
}
};
leetcode142. 环形链表 II
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意,pos 仅仅是用于标识环的情况,并不会作为参数传递到函数中。
- 说明:不允许修改给定的链表。
- 进阶:你是否可以使用 O(1) 空间解决此题?
思路分析
- 哈希表
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
unordered_set<ListNode *> visited;
while (head != nullptr) {
if (visited.count(head)) {
return head;
}
visited.insert(head);
head = head->next;
}
return nullptr;
}
};
- 快慢指针
- 第一次遍历,一快一慢,若相遇,只能确定有环,相遇点可能时环内任意位置;
- 第二次遍历,同速度,相遇点才为环入口点
注意循环的时候边界条件的判断~
相关数学证明,参考官方解答
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
if(head == NULL || head->next == NULL) return NULL;
ListNode *slow = head, *fast = head;
// 注意边界条件的判断
while(fast != NULL && fast->next != NULL){
slow = slow->next;
fast = fast->next->next;
//若找到环,则再次遍历找环入口点
if(slow == fast){
slow = head;
while(slow != fast){
slow = slow->next;
fast = fast->next;
}
return fast;
}
}
return NULL;
}
};
lc287题 寻找重复数,其中一个思路就是通过下标取值,在座位下标,依次往后找,这就转换为了和链表一样的找环入口问题(重复数即为环入口节点)。