PPO算法实现的37个实现细节(1/3)13 core implementation details
博客标题:The 37 Implementation Details of Proximal Policy
Optimization
作者:Huang, Shengyi; Dossa, Rousslan Fernand Julien; Raffin, Antonin; Kanervisto, Anssi; Wang, Weixun
博客地址:https://iclr-blog-track.github.io/2022/03/25/ppo-implementation-details/
代码github仓库地址:https://github.com/vwxyzjn/ppo-implementation-details
文章目录
-
-
- 1. 导言
- 2. 背景
- 3. 复现官方PPO算法的代码实现
-
- 3.1 13 core implementation details
-
- 3.1.1 Vectorized architecture 【Code-level Optimizations】
- 3.1.2 Orthogonal Initialization of Weights and Constant Initialization of biases 【Code-level Optimizations】
- 3.1.3 The Adam Optimizer’s Epsilon Parameter 【Code-level Optimizations】
- 3.1.4 Adam Learning Rate Annealing 【Code-level Optimizations】
- 3.1.5 Generalized Advantage Estimation 【Theory】
- 3.1.6 Mini-batch Updates 【Code-level Optimizations】
- 3.1.7 Normalization of Advantages 【Code-level Optimizations】
- 3.1.8 Clipped surrogate objective【Theory】
- 3.1.9 Value Function Loss Clipping【Code-level Optimizations】
- 3.1.10 Overall Loss and Entropy Bonus【Theory】
- 3.1.11 Global Gradient Clipping【Code-level Optimizations】
- 3.1.12 Debug variables
- 3.1.13 Shared and separate MLP networks for policy and value functions【Code-level Optimizations】
-
1. 导言
Jon 是一名一年级硕士生,对强化学习 (RL) 感兴趣。在他眼中,强化学习似乎很迷人,因为他可以使用 Stable-Baselines3 (SB3) 等强化学习库来训练智能体玩各种游戏。他很快认识到近端策略优化 (PPO) 是一种快速且通用的算法,并希望自己实现 PPO 作为一种学习经验。Jon读完这篇论文后心想:“嗯,这很简单。”然后他打开代码编辑器并开始编写 PPO。 他选择Gym 的 CartPole-v1 作为模拟环境,不久之后,Jon 让 PPO 与 CartPole-v1 一起工作。他度过了一段愉快的时光,并感到有动力让他的 PPO 在更有趣的环境中工作,例如 Atari 游戏和 MuJoCo 机器人任务。 他觉得“那该有多酷啊?”。
然而,他很快就陷入了困境。让 PPO 与 Atari 和 MuJoCo 协同工作似乎比预想的更具挑战性。Jon 随后在网上寻找参考实现,但很快就被淹没了:非官方软件仓库的做法似乎都不一样,而他根本无法读取官方软件仓库中的 Tensorflow 1.x 代码。幸运的是,Jon 偶然发现了两篇解释 PPO 实现的最新论文。"就是它了!"他咧嘴笑道。Jon 无法控制自己的兴奋,开始在办公室里跑来跑去,不小心碰到了 Sam,Jon 知道 Sam 正在研究 RL。他们随后进行了如下对话。
-
“嘿,我刚刚读了 the implementation details matter 和 what matters in on-policy RL 这两篇论文。太有意思了。我就知道
PPO没那么简单!” Jon 感叹道。 -
“哦,是的!
PPO很棘手,我喜欢这两篇深入探讨细节的论文”。Sam 回答道。 -
“的确如此。我觉得我现在更了解
PPO了。你一直在使用PPO,对吧?考考我关于PPO的知识吧!” Jon 热情地问道。 -
“当然。如果你用
Atari游戏Breakout运行官方的PPO代码,agent将在大约 4 小时内获得 400 左右的游戏分数。你知道PPO是如何做到这一点的吗?” -
“emmmm…这其实是个好问题。不过我认为这两篇论文似乎不能解释这个问题。”
-
procgen的论文包含使用官方
PPO和LSTM结合进行的实验。你知道PPO + LSTM是如何工作的吗? -
“emmmm……我没有读过太多关于
PPO + LSTM的文章。” Jon 承认到。 -
“官方
PPO还适用于MultiDiscrete动作空间,在这个动作空间定义下你可以使用multiple discrete values描述一个动作。你知道那是怎么运作的吗?” -
“……” Jon 无言以对。
-
“最后,如果您只有标准工具(例如
numpy、gym…)和神经网络库(例如torch、jax…),您可以从头开始编写PPO算法的代码吗? -
“噢,我想这会很困难。之前的论文分析了
PPO算法的实现细节,但没有展示这些部分是如何编码实现的。另外,我现在意识到他们的结论是在MuJoCo任务中得出的,并不一定会迁移到其他游戏(例如Atari)上。我现在感到很难过……” Jon 叹了口气。 -
“别难过。
PPO算法是一头复杂的野兽。如果有什么帮助的话,我一直在制作有关从头开始实现PPO算法的视频教程以及更深入地解释PPO算法实现细节的博客文章!”

博客文章就在这里!这篇博文没有进行消融研究并就重要细节提出建议,而是退后一步,重点关注PPO算法 in all accounts 中的结果复制。具体来说,这篇博文通过以下方式补充了之前的工作: -
代码实现的清单及参考资料:在重新复现过程中,我们编制了一份包含 37 个细节的代码实现清单,如下所示。
- 13 core implementation details
- 9 Atari specific implementation details
- 9 implementation details for robotics tasks (with continuous action spaces)
- 5 LSTM implementation details
- 1 MultiDiscrete action spaces implementation detail
-
可复现性高:为了验证我们的复现效果,我们在经典控制任务、 Atari、MuJoCo 任务、LSTM 和实时战略(RTS)游戏任务中证明了我们的实现与原始实现的结果非常吻合。
-
额外的实现细节:我们还介绍了 4 个官方代码实现中没有使用但在特殊情况下可能有用的代码实现细节。
我们的最终目的是帮助人们透彻理解 PPO 的代码实现,高保真地再现过去的结果,并为新研究的定制提供便利。为了使研究具有可复制性,我们在以下网站提供了源代码: https://github.com/vwxyzjn/ppo-implementation-details 可在以下网站获取实验结果:https://wandb.ai/vwxyzjn/ppo-details
2. 背景
PPO算法是 Schulman 等人(2017)提出的一种策略梯度算法。作为信任区域策略优化 (TRPO)(Schulman 等人,2015)的改进,PPO 使用更简单的修剪替代目标clipped surrogate objective,省略了 TRPO 中提出的昂贵的二阶优化second-order optimization。尽管目标objective更简单,但 Schulman 等人 (2017) 表明,在许多控制任务中,PPO 比 TRPO 具有更高的样本效率。 PPO 在包含 Atari 游戏的街机学习环境(ALE)中也具有良好的实证表现。
为了促进更透明的研究,Schulman 等人(2017)在 openai/baselines GitHub 存储库中提供了 PPO 的源代码,代码名为 pposgd(于 7/20/2017 提交 da99706)。后来,openai/baselines 维护者推出了一系列修订。关键事件包括:
- 2017年11月16日,提交
2dd7d30:维护者引入了重构版本ppo2,并将pposgd重命名为ppo1。根据 GitHub 问题,一位维护者建议ppo2应通过批量处理来自多个模拟环境的观察结果来提供更好的GPU利用率。 - 2018 年 8 月 10 日,提交
ea68f3b:经过几次修改后,维护者评估了ppo2,进行了MuJoCo基准测试。 - 2018 年 10 月 4 日,提交
7bfbcf1:经过几次修改后,维护者评估了ppo2,产生了Atari游戏的基准。 - 2020 年 1 月 31 日,提交
ea25b9e:维护者已将迄今为止的最后一次提交合并到openai/baselines中。据我们所知,ppo2(ea25b9e) 是许多PPO相关资源的基础:Stable-Baselines3 (SB3)、pytorch-a2c-ppo-acktr-gail和CleanRL等RL库已经构建了其PPO实现,以紧密匹配ppo2 (ea25b9e)中的实现细节。- 最近的论文(Engstrom、Ilyas 等人,2020 年;Andrychowicz 等人,2021 年)研究了
ppo2 (ea25b9e)中有关机器人任务的实现细节。
近年来,复现 PPO 算法的结果已成为一个具有挑战性的问题。下表收集了 Atari 和 MuJoCo 环境中流行 RL 库中 PPO 算法的最佳性能总结。

我们提出几点看法。
openai/baselines中的这些修订并非没有性能影响。复现 PPO 的结果具有挑战性,部分原因是即使最初的实现也可能产生不一致的结果。ppo2 (ea25b9e)和与其实现细节相匹配的代码库展现了相当相似的结果。相比之下,其他代码库通常的结果更加多样化。- 有趣的是,我们发现许多库展示了
MuJoCo任务的性能,但没有报告Atari任务的性能。
尽管情况很复杂,我们还是发现 ppo2 (ea25b9e) 是一个值得研究的实现。它在 Atari 和 MuJoCo 任务中都获得了良好的性能。更重要的是,它还融合了 LSTM 等高级功能和多离散动作空间MultiDiscrete action space的处理,解锁了实时策略游戏等更复杂游戏的应用。因此,我们将 ppo2 (ea25b9e) 定义为官方 PPO 实现,并将本博客文章的其余部分基于此实现。
3. 复现官方PPO算法的代码实现
在本节中,我们将介绍五类实现细节,并在 PyTorch 中从头开始实现它们。五类实现细节分别是:
- 13 core implementation details
- 9 Atari specific implementation details
- 9 implementation details for robotics tasks (with continuous action spaces)
- 5 LSTM implementation details
- 1 MultiDiscrete implementation detail
对于每个类别(第一个类别除外),我们在三个环境中将我们的实现与原始实现进行基准测试,每个环境都有三个随机种子。
3.1 13 core implementation details
我们首先介绍 13 个常用的核心实现细节,这些细节与任务无关。为了帮助理解如何在 PyTorch 中对这些细节进行代码编写,我们准备了如下逐行视频教程。请注意,视频教程在制作过程中跳过了第 12 和第 13 个实现细节,因此视频的标题是 “11 个核心实现细节”。
视频链接:https://www.bilibili.com/video/BV1YB4y1R78s
3.1.1 Vectorized architecture 【Code-level Optimizations】
PPO 利用一种称为矢量化架构Vectorized architecture的高效范例,该架构的特点是单个学习器可以收集样本并从多个环境中学习。下面是伪代码:
envs = VecEnv(num_envs=N)
agent = Agent()
next_obs = envs.reset()
next_done = [0, 0, ..., 0] # of length N
for update in range(1, total_timesteps // (N*M)):
data = []
# ROLLOUT PHASE
for step in range(0, M):
obs = next_obs
done = next_done
action, other_stuff = agent.get_action(obs)
next_obs, reward, next_done, info = envs.step(
action
) # step in N environments
data.append([obs, action, reward, done, other_stuff]) # store data
# LEARNING PHASE
agent.learn(data, next_obs, next_done) # `len(data) = N*M`
在这种架构中,PPO 首先初始化一个矢量化环境 envs,然后利用多进程技术依次或并行运行 N 个(通常是独立的)环境。(通常是独立的)环境,这些环境可以顺序运行,也可以利用多进程并行运行。envs 提供了一个同步接口,它总是从 N个观测数据环境中的 N 个观察结果,并通过 N个行动来步进 N个环境。当调用 next_obs = envs.reset() 时,next_obs 会获取一批 N个初始观测值(读作 "next observation")。PPO 还会将环境完成标志变量 next_done(读作 "next done")初始化为一个长为N的零数组,其中第 i 个元素 next_done[i]的值为 0 或 1,分别对应第 i个子环境分别为 "未完成 "和 “已完成”。
然后,矢量化架构循环两个阶段: rollout phase 和 learning phase:
rollout phase:agent对 N 个环境的动作进行采样,固定的交互采样 M个steps。在这 M 次采样期间,agent会持续将相关数据添加到空列表数据中。如果第 i 个子环境在执行了第 i 个动作 action[i] 之后done(terminated or truncated),envs 会将其返回的 next_done[i] 设为 1,并自动重置第i个子环境,并在 next_obs[i] 中填入第 i 个环境中新的初始episode中的初始观测值。
learning phase: agent从rollout phase收集的数据中学习:长度为 NM 的数据、next_obs 和 done。具体来说,PPO 可以根据 next_done 估算下一个观测值 next_obs 的值,并计算优势值 advantages 和回报值returns,这两个值的长度也是 NM。然后,PPO 从准备好的数据 [data、advantages、returns]中学习,这被 Schulman 等人称为 "fixed-length trajectory segments"(Schulman et al.)
了解 next_obs 和 next_done 在阶段间转换方面的作用非常重要:在第j个rollout phase的最后,next_obs可以被用来估计 learning phase 的最后一个状态的价值并且可以作为第j+1个rollout phase的开始, next_obs变成data中的初始observation。同样,next_done 告诉 next_obs 是否实际上是新episode的第一个observation。这种复杂的设计允许 PPO 继续步进子环境,并且因为agent总是从 M个steps之后的固定长度轨迹段中学习,即使子环境永远不会终止或截断,PPO 也可以训练agent。这基本上就是为什么 PPO 可以在单个episode中持续 100,000 steps (default truncation limit for Atari games in gym) 的长视野 long-horizon 游戏中学习的原因。
一种常见的错误实现是根据episodes 训练 PPO 并设置最大episodes 范围。下面是伪代码。
env = Env()
agent = Agent()
for episode in range(1, num_episodes):
next_obs = env.reset()
data = []
for step in range(1, max_episode_horizon):
obs = next_obs
action, other_stuff = agent.get_action(obs)
next_obs, reward, done, info = env.step(action)
data.append([obs, action, reward, done, other_stuff]) # store data
if done:
break
agent.learn(data)
这种方法有几个缺点。首先,这种方法可能效率不高,因为agent在每个step中都必须进行一次前向传递。其次,它无法扩展到更大范围的游戏,如《星际争霸 II》(SC2)。星际争霸2的一个episode可能会持续 100,000 步,这就增加了对内存的需求。
矢量化架构通过学习固定长度的轨迹片段来处理这 100,000 步。如果我们设置 N=2 和 M=100,agent将从 2 个独立环境的前 100 个steps中学习。然后,注意 next_obs 是来自这两个环境的第 101 个观测值,agent可以继续doing rollouts,从这两个环境的 101 步到 200 步进行学习。从本质上讲,agent每次学习一个episode的一部分也就是M个steps。
Andrychowicz, et al. (2021)提出N 是 num_envs (decision C1) and M∗N 是 iteration_size (decision C2) , 他建议增加 N (such as N=256) 增加吞吐量但是会导致performance变差. 他们认为性能下降是由于“shortened experience chunks” (M变小了因为N增大了) 和“earlier value bootstrapping”。
3.1.2 Orthogonal Initialization of Weights and Constant Initialization of biases 【Code-level Optimizations】
翻译:权重的正交初始化和偏差的恒定初始化
相关代码位于 openai/baselines 库中的多个文件中。一般来说,隐藏层的权重使用缩放 np.sqrt(2) 的权重正交初始化,并且偏差设置为 0,如针对 Atari 环境的 CNN 初始化所示,以及针对 Mujoco 环境的 MLP 初始化。然而,policy output layer权重的初始化范围为 0.01,value output layer权重初始化为 1。
看来openai/baselines (a2c/utils.py#L20-L35) 的正交初始化的实现与pytorch/pytorch (torch.nn.init.orthogonal_) 的不同。但是,我们认为这是一个非常低级的细节,不应影响性能。
Engstrom、Ilyas 等人 (2020) 发现正交初始化在实现highest episodic return方面优于默认的 Xavier 初始化。此外,Andrychowicz 等人(2021) 发现将动作分布集中在 0 附近(即用 0.01policy output layer权重)是有益的。
3.1.3 The Adam Optimizer’s Epsilon Parameter 【Code-level Optimizations】
PPO 将 epsilon 参数设置为 1e-5,这与 PyTorch 中的默认 epsilon 1e-8 和 TensorFlow 中的默认 epsilon 1e-7 不同。我们列出这个实现细节是因为 epsilon 参数既没有在论文中提到,也不是 PPO 实现中的可配置参数。虽然这个实现细节可能看起来过于具体,但重要的是我们将其匹配以实现高保真再现。
安德里霍维奇等人(2021) 对 Adam 优化器的参数进行网格搜索(决策 C24、C26、C28)并建议β1=0.9并使用 Tensorflow 的默认 epsilon 参数 1e-7。Engstrom, Ilyas, et al., (2020) 使用默认的 PyTorch epsilon 参数 1e-8。
3.1.4 Adam Learning Rate Annealing 【Code-level Optimizations】
翻译:Adam 学习率退火(衰减)
Adam 优化器的学习率可以是恒定的,也可以设置为衰减。默认情况下,玩 Atari 游戏的训练agent的超参数将学习率设置为随着时间步数的增加从 2.5e-4 线性衰减到 0。在 MuJoCo 中,学习率从 3e-4 线性衰减到 0。
Engstrom、Ilyas 等人 (2020) 发现 Adam 学习率退火可以帮助智能体获得更高的情景回报。此外,Andrychowicz 等人(2021) 还发现学习率退火很有帮助,因为它提高了所检查的 5 个任务中的 4 个的性能,尽管性能提升相对较小。
3.1.5 Generalized Advantage Estimation 【Theory】
尽管 PPO 论文在 PPO 的目标中使用了优势估计advantage estimate 这一抽象概念,但 PPO 的实现确实使用了广义优势估计Generalized Advantage Estimation 。两个重要的小细节:
- Value bootstrap:
如果一个子环境没有被终止或截断terminated or truncated,PPO 会估计该子环境中下一个状态的value作为 value target。
关于truncated的说明: 几乎所有gym环境都有时间限制,如果运行时间过长,就会自我截断。例如,CartPole-v1 有 500 steps的时间限制,如果游戏持续超过 500 步,就会返回 done=True。虽然 PPO 实现并不估计截断环境中的最终状态值,但我们(凭直觉)应该这样做。尽管如此,为了高保真再现,我们并没有实现对截断环境的正确处理。
- TD(λ) return estimation:
PPO 实现的 the return target为returns = advantages + values,相当于 TD(λ)用于价值估计(其中蒙特卡洛估计是 λ=1 时的特例)
安德里霍维奇等人(2021) 发现 GAE 的性能优于N-step returns 。
3.1.6 Mini-batch Updates 【Code-level Optimizations】
在矢量化架构的学习阶段,PPO 实现会打乱大小为 N*M 的训练数据的索引并将其分成小批量来计算梯度并更新策略。
一些常见的错误实现包括 1) 始终使用整个批次进行更新,2) 通过从训练数据中随机获取来实现小批量(这不能保证获取所有训练数据点)。
3.1.7 Normalization of Advantages 【Code-level Optimizations】
根据 GAE 计算优势后,PPO 通过减去平均值并除以标准偏差对优势进行归一化处理。特别要指出的是,这种归一化是在小批量而不是整个批量层面进行的!
安德里霍维奇等人(2021)发现每小批量优势标准化不会对性能产生太大影响。
3.1.8 Clipped surrogate objective【Theory】
PPO的 clips the objective 正如论文中所建议的。
Engstrom、Ilyas 等人(2020)发现,当 PPO 控制其他实施细节相同时,PPO 的clipped objective与 TRPO 的 objective具有相似的性能。安德里霍维奇等人(2021)发现 PPO 的clipped objective在大多数任务中优于普通策略梯度(PG)、V-trace、AWR 和 V-MPO。
基于上述发现,我们认为 PPO 的裁剪目标仍然是一个很好的目标,因为它实现了与 TRPO 目标相似的性能,同时计算成本更低(即没有像 TRPO 那样进行二阶优化)。
3.1.9 Value Function Loss Clipping【Code-level Optimizations】
PPO 剪裁价值函数,就像 PPO 剪裁代理目标一样。鉴于V_{targ} = returns = advantages + values,PPO 通过最小化以下损失来拟合价值网络:
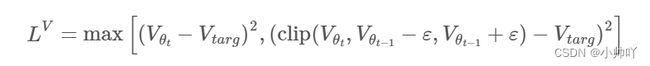
Engstrom、Ilyas 等人 (2020) 没有发现任何证据表明价值函数损失裁剪有助于提高性能。安德里霍维奇等人(2021) 建议价值函数损失裁剪甚至会损害性能。
我们实现了这个细节,因为这项工作更多的是关于先前结果的高保真再现。
3.1.10 Overall Loss and Entropy Bonus【Theory】
总体损失的计算公式为:loss = policy_loss - entropy * entropy_coefficient + value_loss * value_coefficient,这使得熵奖励项最大化。请注意,策略参数和值参数共享相同的优化器。
姆尼赫等人报告了这种熵奖励,通过鼓励动作概率分布稍微随机一些来改善探索。
安德里霍维奇等人总体而言,没有证据表明熵项可以提高连续控制环境的性能。
3.1.11 Global Gradient Clipping【Code-level Optimizations】
对于一个 epoch 中的每次更新迭代,PPO 都会重新调整策略和价值网络的梯度,以便“global l2 norm”(即所有参数的级联梯度范数the norm of the concatenated gradients of all parameters)不超过 0.5。
安德里霍维奇等人(2021) 发现全局梯度裁剪可以提供较小的性能提升。
3.1.12 Debug variables
PPO 实现附带了几个调试变量,它们是
- policy_lose: the mean policy loss across all data points.
- value_loss: the mean value loss across all data points.
- entropy_loss: the mean entropy value across all data points.
- clipfrac: the fraction of the training data that triggered the clipped objective.
- approxkl: the approximate Kullback–Leibler divergence, measured by (-logratio).mean(), which corresponds to the k1 estimator in John Schulman’s blog post on approximating KL divergence. This blog post also suggests using an alternative estimator ((ratio - 1) - logratio).mean(), which is unbiased and has less variance.
3.1.13 Shared and separate MLP networks for policy and value functions【Code-level Optimizations】
默认情况下,PPO 使用由两层 64 个神经元组成的简单 MLP 网络,并使用双曲正切Hyperbolic Tangent作为激活函数。然后,PPO 构建共享 MLP 网络输出的策略头和价值头。下面是伪代码:
network = Sequential(
layer_init(Linear(np.array(envs.single_observation_space.shape).prod(), 64)),
Tanh(),
layer_init(Linear(64, 64)),
Tanh(),
)
value_head = layer_init(Linear(64, 1), std=1.0)
policy_head = layer_init(Linear(64, envs.single_action_space.n), std=0.01)
hidden = network(observation)
value = value_head(hidden)
action = Categorical(policy_head(hidden)).sample()
另外,PPO 也可以通过切换 value_network='copy'参数,使用不同的网络构建策略函数和值函数。伪代码如下
value_network = Sequential(
layer_init(Linear(np.array(envs.single_observation_space.shape).prod(), 64)),
Tanh(),
layer_init(Linear(64, 64)),
Tanh(),
layer_init(Linear(64, 1), std=1.0),
)
policy_network = Sequential(
layer_init(Linear(np.array(envs.single_observation_space.shape).prod(), 64)),
Tanh(),
layer_init(Linear(64, 64)),
Tanh(),
layer_init(Linear(64, envs.single_action_space.n), std=0.01),
)
value = value_network(observation)
action = Categorical(policy_network(observation)).sample()
我们将前 12 个细节和独立网络架构separate-networks architecture 整合在一起,生成了一个独立的 ppo.py(链接),共 322 行代码。然后,我们修改了大约 10 行代码,采用共享网络架构,生成了一个独立的 ppo_shared.py(链接),共有 317 行代码。 ppo.py(左)和 ppo_shared.py(右)的文件差异可以见原博客。
虽然共享网络架构是 PPO 中的默认设置,但独立网络架构在更简单的环境中显然表现更好。共享网络架构的性能较差可能是由于策略和价值函数的目标相互竞争。因此,我们在视频教程中实现了分离网络架构。
