C语言：进制转换以及原码、反码、补码

一、二进制

         其实我们经常能听到2进制、8进制、10进制、16进制这样的讲法，那是什么意思呢？其实2进制、8进制、10进制、16进制是数值的不同表⽰形式⽽已。

         比如：

数值15的各种进制的表⽰形式：

15的2进制：1111

15的8进制：17

15的10进制：15

15的16进制：F

我们重点介绍⼀下⼆进制：

⾸先我们还是得从10进制讲起，其实10进制是我们⽣活中经常使⽤的，我们已经形成了很多尝试：

• 10进制中满10进1

• 10进制的数字每⼀位都是0~9的数字组成

其实⼆进制也是⼀样的

• 2进制中满2进1

• 2进制的数字每⼀位都是0~1的数字组成

二、进制转换

    10进制的123表示的值是123，那这个值究竟是怎么来的呢？其实10进制的每一位是有自己的权重的，10进制的数字从右向左是个位、十位、百位……，分别每一位的权重是 10^0, 10^1, 10^2 ...…… 而每每一位数乘以他的权重值再相加，得到的就是相应的数。

     例如123=3*10^0+2*10^1+1*10^2

2.1 其他进制转10进制的方法

         在此之前先讲讲2进制转10进制，2进制和10进制是类似的，只不过2进制的每⼀位的权重，从右向左是: 2^0, 2^1 , 2^2 ...

如果是2进制的1101，该怎么理解呢？

                                            1*2^0+0*2^1+1*2^2+1* 2^3=13

所以2进制转10进制，只要将每一位的数乘以他对应的权重并相加就可以了！

同理，8进制和16进制转10进制也是通过这样的方法去实现！

结论：其他进制转10进制的方法就是每一位数乘以他的对应权重并相加！

2.2 10进制转其他进制的方法

       先分析10进制转2进制的方法，比如125

       所以10进制转2进制的方法就是，不断地除以2并记录每一次的余数，余数从下往上依次放在一起就是该数字的2进制形式。

     同理，10进制转8进制或者16进制也是不断除以8或者16并记录每一次的余数。

     结论：10进制转其他进制就是将该10进制数不断地除以要转化地进制，并记录每一次的余数，余数从下往上的数放在一起可以了！！

2.3  2进制转8/16进制

       前面介绍了10进制和其他进制的相互转化，我们至少对于10进制非常了解，但如果是除了10进制以外的其他进制之间是如何相互转化的呢？？

2.3.1 2进制转8进制

      8进制的数字每⼀位是0~7的，0~7的数字，假如各⾃写成2进制，最多有3个2进制位就⾜够了，⽐如7的2进制是111，所以在2进制转8进制数的时候，从2进制序列中右边低位开始向左每3个2进制位会换算⼀ 个8进制位，剩余不够3个2进制位的直接换算。

如：2进制的01101011 

换成8换成8进制后，还要在前面加个0，因为0开头的数字会被当成是8进制。

所以2进制的01101011 转化成8进制就是0153！

结论：2进制转8进制时，从2进制序列中从右向左每3位为一组，剩余不够3位的直接为1组，每组的每个数都分别乘以他的权重值并相加，最后每组得到的数放在一起，就得到了该数8进制的表示形式，别忘记了8进制形式要以0开头！！

2.3.2 2进制转16进制

      16进制的数字每⼀位是0~9,a ~f 的，0~9,a ~f的数字，各⾃写成2进制，最多有4个2进制位就⾜够了， ⽐如 f 的⼆进制是1111，所以在2进制转16进制数的时候，从2进制序列中右边低位开始向左每4个2进制位会换算⼀个16进制位，剩余不够4个⼆进制位的直接换算。

如：2进制的01101011

换成16进制：0x6b，16进制表⽰的时候前⾯加0x

结论：2进制转16进制时，从2进制序列中从右向左每4位为一组，剩余不够4位的直接为1组，每组的每个数都分别乘以他的权重值并相加，最后每组得到的数放在一起，就得到了该数16进制的表示形式，别忘记了16进制形式要以0x开头！！

三、原码、反码、补码

     我们知道，在计算机中，数据信息都是以二进制的方式去存储的，本章了解的是整数的2进制表示形式！

      整数的2进制表示方法有三种，即原码、反码和补码

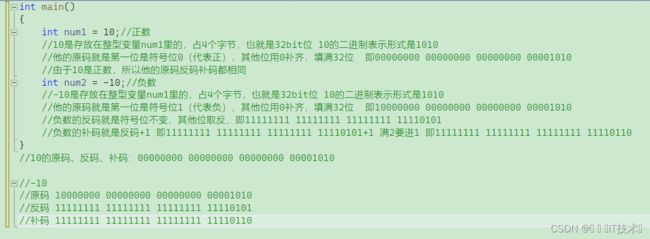
       三种表示⽅法均有符号位和数值位两部分，符号位都是⽤0表⽰“正”，⽤1表⽰“负”，⽽数值位 最⾼位的⼀位是被当做符号位，剩余的都是数值位。

      正整数的原、反、补码都相同。

      负整数的三种表示方法各不相同。

原码：直接将数值按照正负数的形式翻译成⼆进制得到的就是原码。

反码：将原码的符号位不变，其他位依次按位取反就可以得到反码。

补码：反码+1就得到补码。

补码得到源码可是可以使用取反，+1的操作

对于整形来说：数据存放内存中其实存放的是补码，参与计算的也是补码。

为什么呢？？？

    1、  在计算机系统中，数值⼀律⽤补码来表⽰和存储。原因在于，使⽤补码，可以将符号位和数值域统⼀ 处理； 同时，加法和减法也可以统⼀处理（CPU只有加法器）；

    2、  此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

怎么去理解上面2条优势呢？？

上图例子解释了补码的第1个优势：使⽤补码，可以将符号位和数值域统⼀处理。

上图可以解释补码的第2个优势：补码与原码相互转换，其运算过程取反，+1。

四、移位操作符

<< 左移操作符

>> 右移操作符

注：移位操作符的操作数只能是整数。

注：对于移位运算符，不要移动负数位（比如num>>-1），这是标准未定义的！！

4.1 左移操作符

移位规则：左边抛弃、右边补0

4.2 右移操作符

移位规则：⾸先右移运算分两种

1. 逻辑右移：左边⽤0填充，右边丢弃

2. 算术右移：左边⽤原该值的符号位填充，右边丢弃

右移到底是逻辑右移还是算数右移，取决于编译器的实现。大部分的编译器是算数右移。

为什么呢？？？

对于正数10来说，左边的符号位恰好是0，所以无论是算数右移还是逻辑右移，其结果是一样的！

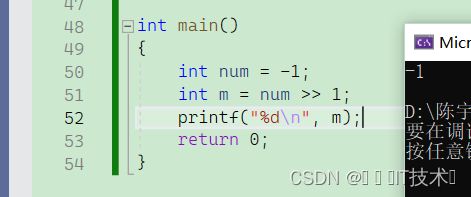
那么对于负数-1，算数右移和逻辑右移就存在差异了！

-1补码逻辑右移后得到的是补码01111111 11111111 11111111 11111111 

由于首位是0，所以该数位正整数，整数的原码反码补码都相同    即2147483647

-1补码算数右移后得到的是补码11111111 11111111 11111111 11111111 

通过取反加1转化10000000 00000000 00000000 00000001     即-1

通过以上比较我们可以发现，负整数的逻辑右移会导致该负数变号！这也是为什么大多数编译器都是采用算数右移！

4.3 为什么int类型的范围是-2147483648 ~ 2147483647？

我们知道int类型是32个比特位，那么int范围是多大呢？？

       首先我们知道整数二进制的三种表现形式是原码、反码、补码，最高的1位是符号位，其余31位代表数字位。

      因为在计算机内部，整数是以二进制形式存储的，而要想让二进制数值表达「负数」的概念，就需要一位标志位。计算机中采用了上文所述的最高位标志位。

      那么很显然当符号位为0且后面31位的数值位都为1时，即011111111 11111111 11111111 11111111为最大值，转化成10进制就是2147483647

       当符号位为1且后面31位的数值位都为1时，即111111111 11111111 11111111 11111111为最大值，转化成10进制就是-2147483647

     那范围不应该是-2147483647——2147483647吗？？

     这是因为，10000000 00000000 00000000 00000000可以用来表示 -0，但这与 0 的二进制表示法 00000000 00000000 00000000 00000000不同，造成了 0 有两种表示方法，使得二进制与十进制的互换不再是一一对应的关系。因此约定了其中的一种方法表示为 -2147483648，所以负数的最小值绝对值比整数的最大值绝对值多 1！！

     通过上述代码，我们可以发现通过1<<31来找到最小整数-2147483648，通过（1<<31）-1来找到最大整数2147483647。可以应用在实际编程中。

4.4 为什么unsigned int类型的范围是 0~4294967295？？

     unsign int 和int的区别就是，他会把int的符号位也当成是数值位，没有符号位所以默认是正数，最小值是0，而32位的数值位使得他的数值可以达到最大，相比较int的31个数值位，当每个数值位取1的时候（即111111111 11111111 111111111 111111111），unsigned int比int多了一个2^32次方的权重，最大值可以达到4294967295！

五、位操作符

& 按位与          只要有0就是0，两个同时为1才是1

|  按位或           只要有1就是1，同个同时为0才是0

^  按位异或       相同为0，相异为1

~ 按位取反        每一位都取反（0->1,1->0）

注：他们的操作数必须是整数，并且是二进制形式。

 六、移位操作符和位操作符的综合应用

6.1 不能创建临时变量（第三个变量），实现两个整数的交换。

第一种写法：

第一种写法确实实现了交换，但是有缺陷：假设a和b相加的结果超出的int整型的范围，那么a+b赋值给a时必然导致某些位的丢失。所以对于一些大的数是不适用的！！

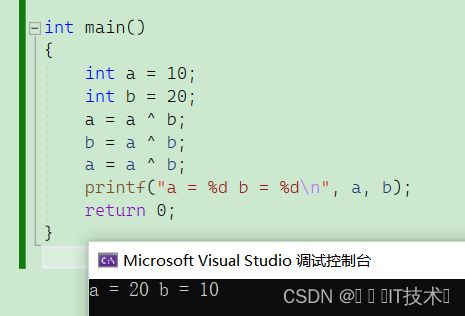
第二种写法

首先异或操作符的特点是相同为0，相异为1，通过这个特点我们可以得到以下公式

a^a=0

a^0=a

即     两个相同的数异或为0，1个数和0异或得到的还是那个数

将第一步的a=a^b代入第二步 即b=a^b^b=a

将第一步的a=a^b代入第三步 即a=a^b^a=b

 通过上述的例子，我们可以把a^b当成是一个密码，这个密码如果和其中一个数异或会得到另一个数！

第二种写法比第一种写法更为通用，因为按位异或操作符只遵循相同为0，相异为1，并不会发生进位，也就不可能出现位数丢失的情况！大数也同样适用！

6.2 编写代码实现，求一个整数存储在内存中的二进制中的1的个数。

6.2.1 思路1

假设在没学习移位操作符和位操作符之前，要怎么思考？

假设我们想求10进制的123中1的个数

123%10拿到个位3,在/10得到12，%10得到十位2，再/10得到1，再%10得到百位1

我们发现要发现计算10进制中的1的个数，就需要取到每一位去判断。

方法就是%10后判断，/10去掉该位数，%10后判断，/10去掉该位数…………

所以我们可以类比得到求2进制中1的个数

方法就是%2后判断，/2去掉该位数，%2后判断，/2去掉该位数…………

      但我们发现输入-1得到的结果是错的，这里需要考虑负数的问题，所以我们要想统计负数的二进制1的个数，需要用到unsign int 因为unsign int 会把符号位也当成数值位，所以-1 的二进制编码为11111111 11111111 11111111 11111111每一位均为数值位得到4294967295，可以进行%10和/10的操作！

6.2.2 思路2

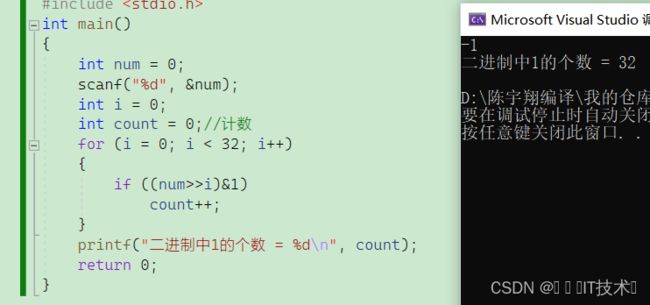
通过学习了位操作符和移位操作符，可以有这样的思路。

&的特点是有0就是0，全为1才是1,通过这个特点我们可以得到以下方法

a&1==1 说明a的最低位是1

a&1==0 说明a的最低为是0

      当我通过&1判断完a的最低位后，将a右移1位接着&1判断，最多移动31次，就可以判断a的每一位是0还是1，从而进行统计。

      我们发现相比思路1，思路2的优势是这里并不需要考虑正负数！因为这两个操作符都是直接在二进制位上进行操作！

6.2.3 思路3

这个思路的前提是，解析n=n&（n-1）

n=n&（n-1）的效果是把二进制中的最后一个1去掉。

当去掉所有的1，n就变成0了。因此我们只需要判断n在变成0之前，n=n&（n-1）执行了几次，就可以知道1的个数了！

6.3   判断一个数是否是2的次方数（n=n&（n-1）的知识迁移）

将2的次方数转化成二进制    2^0=1=0000    2^1=2=0010  2^2=4=0100…………

我们发现2的次方数的二进制形式只会有1个1，所以如果n&（n-1）==0 那么n必然是2的次方数

6.4 二进制位的置0或者置1

将13二进制序列的第5位该成1，然后再改回0.、

第一步：

13的二进制为00000000 00000000 00000000 00001011

要把第5位的0改成1，如果该位能 | 1就可以了，但是同时也要保证其他位不变

所以13必须 |上00000000 00000000 00000000 00010000 

该数可以通过1左移4位得到

所以   n=13 | （1<<4）  即可将其第5位改成1

第二步：

要将第一步的n  000000000 00000000 00000000 00011011的第5位的1再改回0

即把该位&0即可，但是也要保证其他位不变

所以n必须 & 上111111111 111111111 11111111 11101111

该数可以通过~(1<<4)获得

所以   m=n &~(1<<4)    即可将第5位变回0

七、移位操作符和位操作符的一些总结

a&1==1说明a的最低位是1

a&1==0说明a的最低位是0

n&（n-1）每执行一次就可以将n中较为低位的1去掉

想把2进制某一位置1，考虑使用 | 运算符

想把2进制某一位置0，考虑使用 & 运算符和~运算符

a^a=0

a^0=a

a^b ^b=b

a^b ^a=a

想找到int类型的最小值 1<<31

想找到int类型的最大值 （1<<31）-1