数据结构:栈与队列之迷宫(详解)
目录
1.问题描述
2.算法思路
2.1具体需要哪些数据
2.2路径的查找
2.3输出迷宫路径
2.4通俗的解释
3.迷宫的构造
4.路径查找
5.打印迷宫路径
6.完整代码
7.总结
1.问题描述
以一个m* n的长方阵表示迷宫,0和1分别表示迷宫中的通路和障碍。设计一个程序,对任意设定的迷宫,求出一条从入口到出口的通路,或得出没有通路的结论。
2.算法思路
2.1具体需要哪些数据
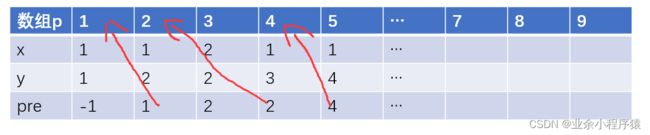
设置一个结构体数组,里面有x,y,和pre,分别是坐标和前驱结点数(也就是这个pre数是来源于前面哪个相同迷宫位置,就比如前面结点为(5,6)存在数组中位置是10,那如果要存(5,7)这个点,那么这是这个点的前驱结点就是pre=10);
再设置一个二维数组mark和迷宫大小一样来标记这个点是不是已经存过或者是障碍。
迷宫搜索的时候可以有八个方向,上下左右和它的四个对角,这里需要用一个二维数组Direction来存储每次要走的八个方向。
2.2路径的查找
我们从起点出发,每次查找当前的八个方向是否有路可以走,如果有路走就存在结构体数组中点x和y,以及该点当前在数组中的位置(也就是可以走的这一点的前驱pre),当前的点八个方向找完后,就找下一个可以走的点的八卦方向,一直到终点为止,否正就是迷宫没有解。
2.3输出迷宫路径
从终点出发进行查找,先找的终点的前驱在数组的第几位,然后根据每个找到点的前驱,一直到起始点为止。
就比如这条路径就是(1,1)——>(1,2)——> (1,3)——>(1,4)......
2.4通俗的解释
就是把所有可以走的路全存在了数组中,然后从终点的结点按照它的前驱来找其前面一个点,直到找到起始点。因为我们一开始就是从起始点开始存的,所以每个点的最终前驱都是起始点。所以从终点出去回溯查找的必然也是起始点。
3.迷宫的构造
迷宫的外围都是设置为1,作为迷宫的围墙。里面就随机生成0或者1作为通道或者作为障碍。实现代码如下所示:
int maze[100][100]; //最大迷宫大小
for(i=0;i4.路径查找
int path(int maze[][100],int m,int n)
{
int dir1,dir2,i; //dir1是上下,dir2是左右方向
p[num].x=1; //起始点
p[num].y=1;
p[num].pre=-1; //起始点前驱为-1
mark[p[num].x][p[num].y]=1; //标记起始点以及存储
num++; //存储后数组数量+1
while(count<=num){ //count为当前的查找结点为止,num为总的数组大小
int x1=p[count].x; //如果当前为止数字在数组中大于总数量大小,则说明没找到
int y1=p[count].y;
for(i=0;i<=7;i++) //找八个方向可以走的路径
{
dir1 = Direction[i][0];
dir2 = Direction[i][1];
if(maze[x1+dir1][y1+dir2]==0&&(!mark[x1+dir1][y1+dir2]))
{ //如果找到方向这个点没有被标记,且不是障碍物,则进行存储
p[num].x=x1+dir1;
p[num].y=y1+dir2;
p[num].pre=count; //存当前为止count结点为止,也是该查找为止的前驱
mark[x1+dir1][y1+dir2]=1; //标记以及存储过
num++; //数组大小加1
if(x1+dir1==m&&y1+dir2==n) //如果是终点,就停止
return 1;
}
}
count++; //当前为止加1,准备找下一个路径
}
return 0;
}5.打印迷宫路径
void print(int maze[][100],int m,int n){
int q = num-1, i=0; //p:寻找从出口到入口过程中行走的路径 i:计数
line a[1001]; //储存完整路径
while(q!=-1){//查找时只要没到入口及一直回退
a[i].x = p[q].x;
a[i].y = p[q].y;
i++;
q = p[q].pre;
}
i--;
while(i>=0){//从入口到出口打印路径
printf("(%d %d)",a[i].x,a[i].y);
i--;
}
}6.完整代码
#include
#include
int count; //前一个点的位子
int num; //当前点的位置或者数量
int mark[100][100];
int Direction[8][2] = {{1,0},{1,1},{0,1},{-1,1}, {-1,0},{-1,-1},{0,-1},{1,-1} }; // 八个方向的偏移量 (逆时针)
typedef struct{
int x,y,pre;
}line;
line p[10000];
int path(int maze[][100],int m,int n)
{
int dir1,dir2,i; //dir1是上下,dir2是左右方向
p[num].x=1; //起始点
p[num].y=1;
p[num].pre=-1; //起始点前驱为-1
mark[p[num].x][p[num].y]=1; //标记起始点以及存储
num++; //存储后数组数量+1
while(count<=num){ //count为当前的查找结点为止,num为总的数组大小
int x1=p[count].x; //如果当前为止数字在数组中大于总数量大小,则说明没找到
int y1=p[count].y;
for(i=0;i<=7;i++) //找八个方向可以走的路径
{
dir1 = Direction[i][0];
dir2 = Direction[i][1];
if(maze[x1+dir1][y1+dir2]==0&&(!mark[x1+dir1][y1+dir2]))
{ //如果找到方向这个点没有被标记,且不是障碍物,则进行存储
p[num].x=x1+dir1;
p[num].y=y1+dir2;
p[num].pre=count; //存当前为止count结点为止,也是该查找为止的前驱
mark[x1+dir1][y1+dir2]=1; //标记以及存储过
num++; //数组大小加1
if(x1+dir1==m&&y1+dir2==n) //如果是终点,就停止
return 1;
}
}
count++; //当前为止加1,准备找下一个路径
}
return 0;
}
void print(int maze[][100],int m,int n){
int q = num-1, i=0; //p:寻找从出口到入口过程中行走的路径 i:计数
line a[1001]; //储存完整路径
while(q!=-1){//查找时只要没到入口及一直回退
a[i].x = p[q].x;
a[i].y = p[q].y;
i++;
q = p[q].pre;
}
i--;
while(i>=0){//从入口到出口打印路径
printf("(%d %d)",a[i].x,a[i].y);
i--;
}
}
int main()
{
int m,n;
printf("请输入迷宫的大小(行数和列数):");
scanf("%d%d",&m,&n);
int i ,j;
/* int maze[12][12] = {
{1,1,1,1,1,1,1,1,1,1,1,1},
{1,0,1,1,1,0,0,0,0,0,0,1},
{1,0,0,0,1,0,0,0,1,0,0,1},
{1,0,1,0,1,1,0,0,1,0,0,1},
{1,0,1,0,0,1,0,1,1,0,0,1},
{1,0,1,0,0,1,0,1,1,0,0,1},
{1,1,1,1,0,1,0,1,0,0,0,1},
{1,0,0,1,0,0,0,1,0,1,1,1},
{1,0,0,1,0,0,0,1,0,1,1,1},
{1,0,1,1,0,1,0,1,0,0,0,1},
{1,0,0,0,0,1,0,1,1,1,0,1},
{1,1,1,1,1,1,1,1,1,1,1,1} };*/
int maze[100][100];
for(i=0;i 7.总结
迷宫对于数据结构的萌新来说,是比较困难的。所以需要多理解栈和队列的思想,在看这个之前,可以先做做栈和队列其他题目,比如转进制转化等问题,再回来写迷宫问题会更好理解。