NeRF详解
论文标题:《NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis》
论文地址:https://arxiv.org/abs/2003.08934
推荐代码:https://github.com/leviome/NeRF_experiment(由本人整理,代码不解处也欢迎留言讨论,如有帮助请给star~)
文章目录
- 前言
- 隐式表达
- NeRF的训练
-
- 位置编码 (对应原文5.1章节)
- 层次化体采样 (对应原文5.2章节)
- 体渲染(Volume Rendering)
前言
对于三维重建方向的研究人员来说,NeRF的重要性不言自明。NeRF作为ECCV2020的最佳论文提名之一,是值得精读的经典论文之一。不过,NeRF所涉及的图形学知识过多,对于纯CVer阅读起来较为吃力。本文旨在用朴素易懂的概念来解释NeRF的基本原理。如有不明白之处,欢迎留言交流~
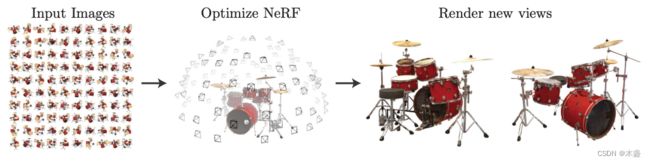
NeRF,全称Neural Radiance Field,即神经辐射场。要了解NeRF,首先要知道NeRF是干嘛的,答:三维场景的新视角合成。NeRF是一种使用神经网络来隐式表达3D场景的技术。
隐式表达
所谓隐式表达,与之相对的就是显式表达。假设我们用NeRF学习了一个确定场景,那么这个场景被隐式地保存在NeRF神经网络的参数中,假如我们需要得到一个新视角的画面,我们需要用神经网络计算出这个画面各个位置的光线和颜色值。
为了更方便理解,我用2D图像表示来举例:
我们有一张2D图像,像素点的坐标是 ( x , y ) (x,y) (x,y),像素点的颜色是 ( r , g , b ) (r,g,b) (r,g,b)。既然坐标和颜色是一一对应的,我们是否可以构建一种映射关系呢?
F Θ ( x , y ) = ( r , g , b ) (1) F_{\Theta}(x,y)=(r,g,b)\tag{1} FΘ(x,y)=(r,g,b)(1)
这种映射关系可以被神经网络来表达:
( x , y ) → N N → ( r , g , b ) (2) (x,y)\rightarrow NN \rightarrow (r,g,b)\tag{2} (x,y)→NN→(r,g,b)(2)
我们可以对图像采样一些随机点当作神经网络的训练数据,然后可以用训练好的神经网络来推理这张图像其他位置像素值。这里很好理解,我们直接将这种情况推广到3D,就可以得到NeRF的基本结构。NeRF的公式表达:
F Θ : ( x , d ) → ( c , σ ) (3) F_{\Theta}:(\bold{x},\bold{d}) \rightarrow(\bold{c},\sigma)\tag{3} FΘ:(x,d)→(c,σ)(3)
式(3)中的 x = ( x , y , z ) \bold{x}=(x,y,z) x=(x,y,z)表示3D点的坐标, d = ( θ , ϕ ) \bold{d}=(\theta,\phi) d=(θ,ϕ)表示观测方向, c = ( r , g , b ) \bold{c}=(r,g,b) c=(r,g,b)表示3D点预测出来的颜色值, σ \sigma σ表示体密度(一会儿着重解释)。我们对比式(1)和式(3)可以发现一些区别,由平面推广到3D要考虑很多东西,首先一点就是观测角度会影响3D点的颜色表现。所以,整个NeRF的设计就是一套view-dependent的思路,所以NeRF的输入除了3D位置以外,还需要观测角度,一共需要5D向量作为输入,即 ( x , y , z , θ , ϕ ) (x,y,z,\theta,\phi) (x,y,z,θ,ϕ)。输出结果为该3D点的像素值 c \bold{c} c和体密度 σ \sigma σ,这两个输出可以用来进行体渲染(volume rendering)。
NeRF的训练
要明白NeRF,首先需要了解几个概念。1,什么是camera ray?答:相机射线。

从图2我们可知,NeRF是5D输入 ( x , y , z , θ , ϕ ) (x,y,z,\theta,\phi) (x,y,z,θ,ϕ)和4D输出 ( r , g , b , σ ) (r,g,b,\sigma) (r,g,b,σ)。
多出来的表示观测方向的两个输入参数 ( θ , ϕ ) (\theta, \phi) (θ,ϕ)是什么意思呢?一张图可以解惑:
固定 θ \theta θ改变 ϕ \phi ϕ,再加旋转平移:
固定 ϕ \phi ϕ,改变 θ \theta θ,再加旋转平移:
通过两张gif的转动,大概可以理解 θ \theta θ和 ϕ \phi ϕ分别控制的角度了~ 粗略可以理解为 ϕ \phi ϕ代表俯仰(点头), θ \theta θ代表偏航(摇头)。
如子图(a)所示,对于某已知视图,我们可以对每个2D点作出射线,然后沿着射线的方向(即深度方向)做多个点的采样,至于射线原理不太明白请了解一下相机二维坐标和三维坐标的映射关系(《【AI数学】相机成像之内参数》)。我们可以从下面的动态图获得一个直观感受:
对于公式(1)中所描述的2D图像表示,我们只需要明确像素位置,即可找到对应的颜色值。但对于3D场景表示,我们在某个确定视点看到的2D视图就很难被单一表示出来。因为,确定视点下看到的2D图像是一组图像的加权叠加,而这组图像是你观测视角射线上依次采样出来的,准确来说,2D视图上每一个像素颜色值都是3D场景上在该观测方向的射线上一组采样点的加权叠加。了解到这里,我们可以回头看图(2),先看子图(a),其中黑色的小圆点就是射线上的采样点,每个小圆点就能获得一组9D的训练样本 ( x , y , z , θ , ϕ ; r , g , b , σ ) {(x,y,z,\theta,\phi;r,g,b,\sigma)} (x,y,z,θ,ϕ;r,g,b,σ),可直接用来训练MLP。在推理阶段,我们也需要在观测射线进行采样。
所以,NeRF是用MLP来隐式表达一个场景,它是点对点的表示方式。我们如果想要获得一个新视角的试图,我们则需要获得这个视角下,观测射线上所有采样点的 ( r , g , b , σ ) (r,g,b,\sigma) (r,g,b,σ),假设我们视图的分辨率是224x224的,每个点回引出一条射线(如图r所示),假设每条射线上采样16个点,那我们NeRF中的MLP需要进行224x224x16次推理,得到的结果可以用来进行体渲染。理解这一段相当于懂了NeRF的基本原理。
位置编码 (对应原文5.1章节)
γ ( p ) = ( sin ( 2 0 π p ) , cos ( 2 0 π p ) , ⋯ , sin ( 2 L − 1 π p ) , cos ( 2 L − 1 π p ) ) (4) \gamma(p)=\left(\sin \left(2^0 \pi p\right), \cos \left(2^0 \pi p\right), \cdots, \sin \left(2^{L-1} \pi p\right), \cos \left(2^{L-1} \pi p\right)\right)\tag{4} γ(p)=(sin(20πp),cos(20πp),⋯,sin(2L−1πp),cos(2L−1πp))(4)
位置编码是NeRF中的重要创新点之一,加入位置编码使得NeRF对于新视点重建的效果大大提升。具体效果我们可以看图(5)。其大概原理是,尽量使相邻位置的输出结果不要相似。每个位置输入 x \bold{x} x,经过位置编码以后,与相邻位置具有较大差异。
![]()
P E ( x ⃗ ) = e ⃗ (5) \bold{PE}(\vec{x})=\vec{e}\tag{5} PE(x)=e(5)
关于位置编码,我写了一篇详细的介绍《NeRF中的位置编码》,链接可戳。
层次化体采样 (对应原文5.2章节)
原本的体渲染策略并不高效,因为均匀对待每一个采样点。但是空白区域和遮挡区域并没对渲染图像取到作用。作者采用了一种层次化表示来提升渲染效率。具体做法是:采用两个网络来表示一个场景(一个粗,一个细)。先用普通采样来评估“粗”网络,然后用“粗”网络来制造更有信息量的采样,比如哪些采样点对体渲染更有帮助。
粗采样:在光线上均匀采样,根据体渲染公式获得每个采样点的权重(由体密度和位置远近共同决定);
精采样:根据粗采样获得的权重,做一个光线上的归一化,将权重之和置为1,得到概率密度函数(PDF)。根据PDF来精采样,即让更重要的线段上有更多的采样点。
最后,粗采样和精采样的采样点一起进入体渲染,共同作用得到像素的颜色值。
体渲染(Volume Rendering)
NeRF中最后一个理解难点就是Volume Rendering了,这是一个CG概念。在上面NeRF的训练中,我们得知,NeRF会对每条射线中的每个采样点进行预测,而我们单一新视角的视图中每一个像素点的RGB值需要这一条射线上所有的采样点的 ( r , g , b , σ ) (r,g,b,\sigma) (r,g,b,σ)值来决定。而体渲染就是做了这么一件事,它利用了光吸收的物理模型来表达。
C ( r ) = ∫ t n t f T ( t ) σ ( r ( t ) ) c ( r ( t ) , d ) d t , where T ( t ) = exp ( − ∫ t n t σ ( r ( s ) ) d s ) (6) C(\mathbf{r})=\int_{t_n}^{t_f} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t, \text { where } T(t)=\exp \left(-\int_{t_n}^t \sigma(\mathbf{r}(s)) d s\right) \tag{6} C(r)=∫tntfT(t)σ(r(t))c(r(t),d)dt, where T(t)=exp(−∫tntσ(r(s))ds)(6)
∑ i = 1 N T i α i c i (7) \sum_{i=1}^N T_i \alpha_i c_i\tag{7} i=1∑NTiαici(7)
T i = ∏ j = 1 i − 1 ( 1 − α j ) (8) T_i=\prod_{j=1}^{i-1}\left(1-\alpha_j\right)\tag{8} Ti=j=1∏i−1(1−αj)(8)
α i = 1 − e − σ i δ t i (9) \alpha_i=1-e^{-\sigma_i \delta t_i}\tag{9} αi=1−e−σiδti(9)
公式(5)表示的体渲染的数学模型。实际操作中并不是连续化的,而是采用(6)、(7)、(8)三个公式来执行。
先不急着理解公式,先考虑一个问题:为什么NeRF采用这么麻烦的体渲染?
答:可以从拟合二维视图转变为拟合三维采样点,完成稀疏数据到稠密数据到转换。
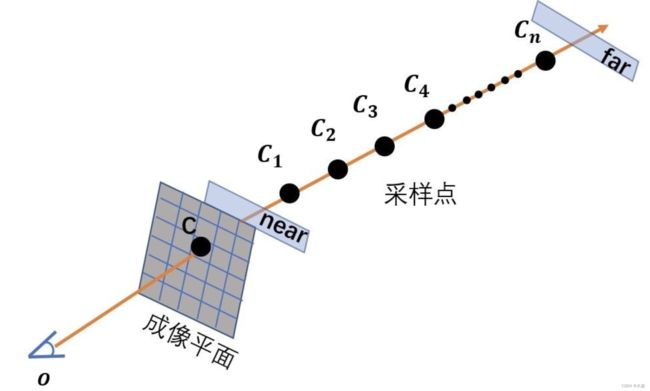
我们要渲染一个新视图时,每个像素点的颜色值都由一条射线(ray)来决定。这条射线的起点就是光心,光心指向二维视图的某个具体像素,便可确定出一条射线,这条射线可以决定这个像素点的颜色值。所以,我们需要获取到这条射线上所有点到颜色和体密度才能确定像素颜色值,通常,我们只会对射线进行采样,由稀疏的采样点的MLP输出来决定这一像素的颜色值。理解这段话以后,我们再来看公式(7-9):体密度大概可以决定该采样点的“重要性”,离光心越近的采样点具有越高的权重。
所以,一个采样点颜色值最后对视图像素采样点颜色值的影响权重是由其体密度和其与光心距离共同决定的。通常,我们会设置一个near和far的边界,很近和很远的采样点我们是不加以考虑的。
如有疑问,欢迎讨论~