一文搞懂哈夫曼树、代码实现及优化（C++版）

✊✊✊大家好！本篇文章将较详细介绍哈夫曼树的相关内容，并对哈夫曼树的构建及相关优化进行代码实现，展示代码语言为：C++代码 。

---

导航小助手

✨一文搞懂哈夫曼树、代码实现及优化（C++版）✨

一、相关知识点

1.完全二叉树

2.完全二叉树的数组表示

3.二叉查找树

4.前中后序遍历

二、代码实现

1.创建单链表

2.二分查找

3.二叉搜索树的实现

---

✨一文搞懂哈夫曼树、代码实现及优化（C++版）✨

一、相关知识点

1.哈夫曼树

 首先，哈夫曼树是最优二叉树，其定义为：给定n个权值作为n个叶子节点，构造一颗二叉树，若树的带权路径长度达到最小，则这棵树被称为哈夫曼树。

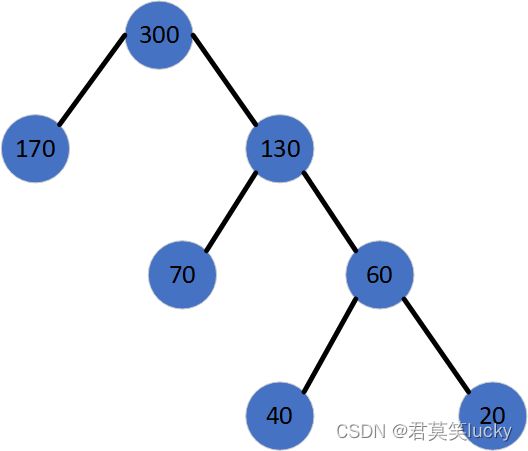
下图就是一颗哈夫曼树：

图1 哈夫曼树示意图

1) 路径和路径长度

定义: 在一棵树中，从一个结点往下可以达到的孩子或者孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

例子: 图1中，170和130的路径长度是1，70和60的路径长度是2，40和20的路径长度是3。

2)结点的权及带权路径长度

定义:若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。

例子: 节点40的路径长度是3，它的带权路径长度= 路径度*权 = 3* 40 = 120.

3)树的带权路径长度

定义: 树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL。

例子: 示例中，树的WPL= 1* 170 + 2*70 + 3*40 + 3*20 = 170 + 140 + 120 + 60 = 490。

哈夫曼树特点总结：

1. 权值越大的叶子结点越靠近根节点。

2. 权值越小的叶子节点越远离根节点。

3. 哈夫曼树并不唯一。

4. 哈夫曼的子树也是哈夫曼树。

5. 哈夫曼树无度为1的结点。

6. 有n个叶子结点的哈夫曼树，总结点数为2n-1。

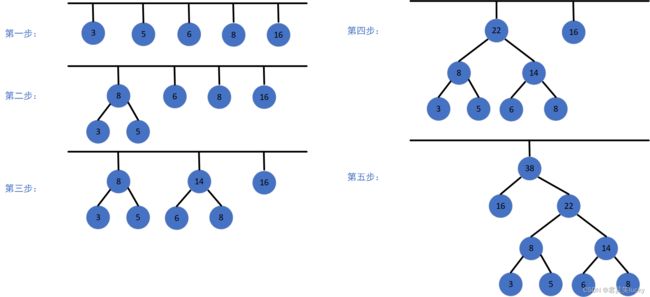
2.哈夫曼树的构造规则

 假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 W1、W2、 ...wn，哈夫曼树的构造规则为:

 1.将w1、w2、...，wn看成是有n 棵树的森林;

 2.在森林中选出根结点的权值最小的两棵树进行合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和;

 3.从森林中删除选取的两棵树，并将新树加入森林;

 4.重复(02)、(03)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树

图2 哈夫曼树构造过程

二、代码实现

1.哈夫曼树

1️⃣ 首先封装好列表类treeNode或者说定义结构体treeNode，包含了权值和左右两个孩子的指针。

//哈夫曼树结点的定义
struct treeNode {
    int weight;//权
    treeNode* lchild;
    treeNode* rchild;
    treeNode(int w, treeNode* l, treeNode* r) {
        weight = w, lchild = l, rchild = r;
    }
};

2️⃣ 哈夫曼树的构造

//创建哈夫曼树
treeNode* build_huffmanTree(vectora) {
    vectorb;
    for (int i = 0; i < a.size(); i++) {
        treeNode* tmp = new treeNode(a[i], NULL, NULL);
        b.push_back(tmp);
    }
    treeNode* l = NULL, * r = NULL, * p = NULL;
    while (b.size() > 1) {
        sort(b.begin(), b.end(), [=](treeNode* A, treeNode* B) {
            return A->weight > B->weight;
            });         //优化：1.两轮冒泡或者选择//2.堆排
        l = b[b.size() - 1];
        b.pop_back();
        r = b[b.size() - 1];
        b.pop_back();
        p = new treeNode(l->weight + r->weight, l, r);
        b.push_back(p);  
    }
    return p;
}

3️⃣  计算WPL-叶子结点的带权路径长度之和

int WPL=0, L = 0;
//基于广度优先搜索实现的层次遍历
void LayerOrder(treeNode* root){
    queueq;
    q.push(root);

    treeNode* last=root;//last代表当前行最右结点 1.
    treeNode* nlast = NULL;//nlast代表下一行最右节点 2.
    while (!q.empty()) {
        treeNode* tmp = q.front();
        cout << tmp->weight << " ";

        if (tmp->lchild == NULL && tmp->rchild == NULL) {
            WPL += tmp->weight * L;
        }//计算WPL
        q.pop();
        if (tmp->lchild != NULL) {
            q.push(tmp->lchild);
            nlast = tmp->lchild;
        }
        if (tmp->rchild != NULL) {
            q.push(tmp->rchild);
            nlast = tmp->rchild;
        }
        if (tmp == last) {
            cout << endl;
            L++;//树高
            last = nlast;
        }
    }
}

效果展示：

完整代码：

#include
#include
#include
#include
using namespace std;

//哈夫曼树结点的定义
struct treeNode {
    int weight;//权
    treeNode* lchild;
    treeNode* rchild;
    treeNode(int w, treeNode* l, treeNode* r) {
        weight = w, lchild = l, rchild = r;
    }
};

template
struct cmp {
    bool operator()(const T& left, const T& right)const {
        return left->weight > right->weight;
    }
};

//创建哈夫曼树
treeNode* build_huffmanTree(vectora) {
    vectorb;
    for (int i = 0; i < a.size(); i++) {
        treeNode* tmp = new treeNode(a[i], NULL, NULL);
        b.push_back(tmp);
    }
    treeNode* l = NULL, * r = NULL, * p = NULL;
    while (b.size() > 1) {
        sort(b.begin(), b.end(), [=](treeNode* A, treeNode* B) {
            return A->weight > B->weight;
            });         
        l = b[b.size() - 1];
        b.pop_back();
        r = b[b.size() - 1];
        b.pop_back();
        p = new treeNode(l->weight + r->weight, l, r);
        b.push_back(p);
    
    }
    return p;
}

//WPL-叶子结点的带权路径长度之和
int WPL，L = 0;
//基于广度优先搜索实现的层次遍历
void LayerOrder(treeNode* root){
    queueq;
    q.push(root);
    
    treeNode* last=root;//last代表当前行最右结点 1.
    treeNode* nlast = NULL;//nlast代表下一行最右节点 2.
    while (!q.empty()) {
        treeNode* tmp = q.front();
        cout << tmp->weight << " ";
        if (tmp->lchild == NULL && tmp->rchild == NULL) {
            WPL += tmp->weight * L;
        }//计算WPL

        q.pop();
        if (tmp->lchild != NULL) {
            q.push(tmp->lchild);
            nlast = tmp->lchild;
        }
        if (tmp->rchild != NULL) {
            q.push(tmp->rchild);
            nlast = tmp->rchild;
        }
        if (tmp == last) {
            cout << endl;
            L++;//树高
            last = nlast;
        }
    }
}

int main() {
    vector a{ 20,40,70,170 };
    treeNode* root = build_huffmanTree(a);
    LayerOrder(root);
    cout << "WPL: " << WPL << endl;
    return 0;
}

2.优先级队列

  哈夫曼树在构建过程中，需先进行两轮排序，选取最小的两棵树作为左、右子树。前文利用sort函数直接进行两轮排序，时间复杂度为O(n^2)，我们可以采用优先队列来进行优化。

  优先级队列的自定义排序的代码实现如下所示：

优先级队列：

#include
#include
#include
using namespace std;

struct node {
    int x, y;
};

template
struct cmp {
    bool operator()(const T& left, const T& right) const{
        return left.x > right.y;
    }
};

int main() {
    //优先队列-底层-堆
    vectora{ {3,4},{1,2},{5,6} };
    //priority_queueq(a.begin(), a.end());//默认大根堆
    //priority_queue,less>q(a.begin(),a.end());//指定大根堆
    //priority_queue, greater>q(a.begin(), a.end());//指定小根堆    
    priority_queue,cmp> q(a.begin(), a.end());
    
    while (!q.empty()) {
        cout << q.top().x << " "<

3.哈夫曼树的优化

将build_huffmanTree函数修改如下：

treeNode* build_huffmanTree(vectora) {
    //优先级队列
    priority_queue,cmp>q;
    for (int i = 0; i < a.size(); i++) {
        treeNode* tmp = new treeNode(a[i], NULL, NULL);
        q.push(tmp);
    }
    treeNode* l = NULL, * r = NULL, * p = NULL;
    while (q.size() > 1) {
        l = q.top();
        q.pop();
        r = q.top();
        q.pop();
        p = new treeNode(l->weight + r->weight, l, r);
        q.push(p);
        //时间从O(n^2)变为O(2logn)
    }
    return p;
}

  优先队列的底层是堆，其时间复杂度为O(2logn)，采用优先队列堆哈夫曼树构造进行优化，能大大减小所需时间。

  本篇文章将较详细介绍哈夫曼树的相关内容，并对哈夫曼树的构建及采用优先队列堆哈夫曼树构造进行优化进行代码实现。

  在《数据结构》专栏，会继续更新其他数据结构的学习内容，感兴趣的小伙伴们可以关注数据结构专栏！        博主水平有限，欢迎大家在评论区或者私信留言交流、批评指正！

更新不易，觉得文章写得不错的小伙伴们，点赞评论关注走一波~~~谢谢啦 ！