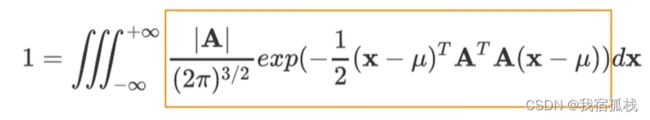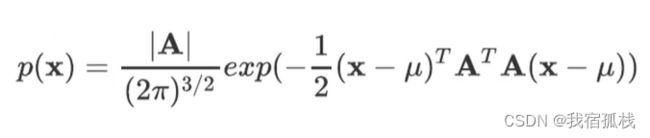3D Guassians Splatting相关解读

从已有的点云模型出发，以每个点为中心，建立可学习的高斯表达，用Splatting即抛雪球的方法进行渲染，实现高分辨率的实时渲染。

1、主要思想

• 1.引入了一种各向异性（anisotropic）的3D高斯分布作为高质量、非结构化的辐射场表达；
  
  从SFM点云出发，以每个点为中心生成3D高斯分布；各向异性指从各个方向看上去都长得不一样，即把一个点往不同相机位姿上投影的时候会投出不一样的样子。

• 2.实现了使用GPU进行快速可微的渲染，允许各向异性的抛雪球（splatting）和快速反向传播；
  
  Splatting：计算机图形学里一个比较经典的用三维点进行渲染的方法，把三维点视作雪球往图像平面上抛，雪球在图像平面上会留下扩散的痕迹，这些点的扩散痕迹叠加在一起构成最后的图像。

• 3.提出了针对3D高斯特性的优化方法，并同事进行自适应密度控制。
  
  除此，存储在点里边的高斯参数需要再反向传播时进行优化更新；
  也会根据梯度自适应地调整点云的分布，如果一个点的3D高斯太大，不能完全拟合该处的细节则对其进行分割操作，用两个点来表达；如果一个位置的点太密集（用不着这么多的3D高斯），则合并为一个3D高斯。

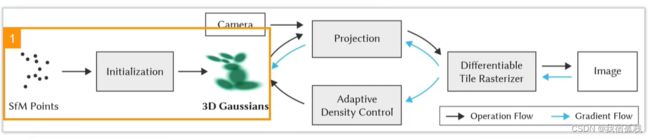
总结：从左边开始对SFM的点云进行初始化得到3D高斯；再沿黑色箭头借助CAMERA的外参做投影Projection，接着用一个可微的光栅化渲染得到图像；再和Nerf一样，把渲染图像和GT图像求loss沿蓝色箭头反向传播，蓝色箭头向上更新3D高斯里的参数，向下送入自适应密度控制更新点云（Adaptive Density Control）。

2、补充预备知识

3D Gaussian

2.1、一维高斯分布的概率密度函数

变量x服从均值为μ，方差为σ²的高斯分布。

2.2、三维高斯分布的概率密度函数

变量为一个向量V，其中三个参数a、b、c均服从均值为0，方差为1的正态分布且相互独立。
一般情况，变量向量x并不一定满足正态分布，则需要将其转换为正态分布，通过矩阵可表示为：

其中均值向量μ中的三个分量分别为xyz各自的均值。向量x的分量各自减去均值即将整个数据的分布去中心化，再通过变换矩阵A对[x, y, z]进行线性组合使其等于[a, b, c]。

变换之后再代入到原式中得到：

到此仍是v的概率密度函数p(v)，再通过以下计算得到x的概率密度函数p(x)：

两边积分得

把dv换成dx，把v换成包含向量x的表达式：

代入可得到：

向量x的概率密度函数即为图中黄色框的一部分：

至此，一维高斯分布通过均值和方差来表示，那么三维对应也应该用均值向量和协方差矩阵来表示，均值上述已经计算得到，下面求解协方差矩阵。

协方差矩阵：

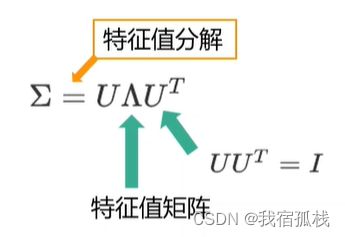
协方差矩阵作为对称矩阵可以进行奇异值分解，上式中的矩阵U每一列都是相互正交的特征单位向量满足UU^T等于单位矩阵I，Λ对角线上的元素是协方差矩阵的特征值，其余元素均为0。

根据行列式性质再转化为：

一组正交基乘以一个对角阵表示一个线性变换。



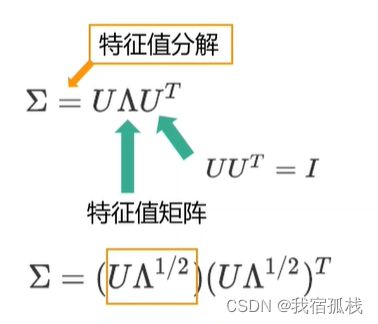
最终的x的概率密度函数p(x)。

3、相关工作

3.1、Point-NeRF（CVPR2022:Point-Based Neural Radiance Fileds）

• 1.为每个点赋予特征向量；
• 2、体渲染时取采样点周边一定领域内的点的特征做线性插值，解码得颜色和体密度；
• 3、自适应点云生长和剔除。
  

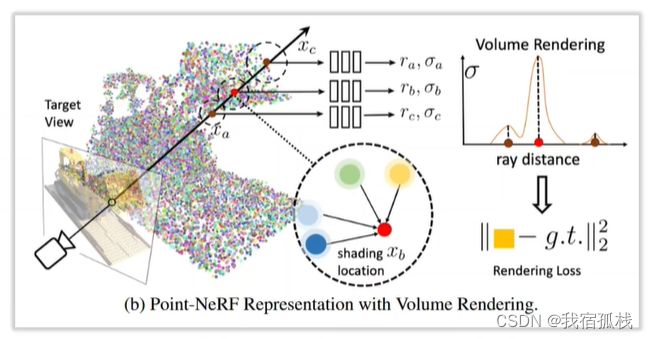
为每个点提取一个特征，储存在点里边；渲染采用体渲染，即从相机光心发出穿透像素的采样射线上取采样点，取采样点周边一定范围内的三维点的特征向量做插值得到采样位置的特征表达；再对特征进行解码得到采样位置的体密度和RGB；再堆叠整条射线上的点得到像素RGB的值。（常见的NerF思路：特征向量、体渲染、插值、解码）

与本文一样由点云出发，构建辐射场，但不同点在于本文点里边存储了物理含义更加明确的3D高斯，避开了Point-NeRF中对抽象特征的学习过程，从而使得训练更容易收敛；在渲染方面，Point-NeRF用体渲染，本文用Splatting更加传统且效率更高。

3.2、Plenoxels(CVPR2022:Radiance Fields without Neural Networks)

体素格点存储球谐函数（spherical harmonic）系数，系数做插值得到采样位置的球谐函数。

继承了NeRF体素、三线性插值和体渲染的要素，抛弃了常用的MLP和隐式特征，直接用更加显示的球谐函数（CG常用），没有神经辐射场。此论文凭此跻身NeRF加速前沿的第一梯队。
本文的3D高斯Splatting的思想和Plenoxels一脉相承，均用尽可能传统但高效的表达方式来提高模型表达能力的下限，再结合一些可微的和可学习的思想来提高模型拟合的上限。简洁优雅效率高。

4、3D Guassian

4.1、可微的3D高斯Splatting

左边绿点即为3D高斯点云，每个点里边存储数据有：
Position(Mean)：默认就有的信息，坐标xyz，也是3D高斯的均值；Covariance matrix，协方差矩阵，椭圆绿球的形状和方向；球谐函数本身即是用一组正交基的线性组合来拟合广场。

为何选择高斯：作者表示是因为需要一种图元能够在拥有场景表达能力的时候可微而且显示地支持快速渲染，因此有了上图所示的3D高斯点云。3D高斯点云中的参数可在迭代优化的过程中更新，也能够很容易地用splat的方法投影到2D图像上做较快的α混合即渲染。

4.11 3D高斯的定义

本文通过协方差矩阵来表达该点，此矩阵控制3D高斯的形状。较之3节中推导的传统表达式，本文中的公式去掉了均值，因为该高斯分布以点为中心，xyz的均值就在点上已经中心化了，所以均值设为0；左侧系数是为控制整个概率密度函数的积分为1，但此处不需要，没有积分为1的限制所以整个分布的大小能够自由控制。

4.12 协方差矩阵的物理含义

A为一个线性变换，把任意一个分布变换到均值为μ方差为1的范围内。二维分布通过图像可表示为：

二维数据通过矩阵A做线性变换，可看作是先在Y方向进行压缩，再绕原点旋转一定角度。
由此，A的构造通常如下：

旋转变换矩阵R，尺度变换矩阵S（对角线上为两个缩放系数）。

本文中的公式：

迭代优化过程中，优化矩阵A的参数即可改变该高斯椭球的形状、大小、方向等等几何外观，从而使其能够在Splatting时投影出正确的效果。

存在问题：

• 1）、旋转矩阵的优化：直接让3*3的旋转矩阵参与优化不可行，所以本文采用四元数参与优化再进行转化，如此便将参数从9个降到了4个，同时能够保持协方差矩阵的半正定性质（ 设A是n阶方阵，如果对任何非零向量X，都有X^TAX≥0，其中X’表示X的转置，就称A为半正定矩阵）。
• 2）、求导：如何让矩阵A对尺度S和四元数q求偏导：论文附录有详细推导；
• 3）、3D高斯如何做渲染（椭球怎样投影成平面的图像）：对鞋方差矩阵做一个变换即可。（该问题在CG领域有较深入研究，本文中引用是一个01年的文献）

4.2、优化和自适应密度控制

4.21 优化

点中存储的参数比如点的位置不透明度、协方差矩阵、球谐函数系数等均参与优化，此优化过程的实现是整个系统正常工作不可或缺的一环。

• 随机梯度下降（Stochastic Gradient Descent）：优化策略
• CUDA核心：写了部分CUDA核心用以加速
• 快速光栅化：提高效率
• Sigmod和Expotential激活函数：不透明度通过Sigmoid函数限制在[0, 1)之内，协方差中的尺度用指数激活函数
• 损失函数：L1loss是渲染图像和GT图像求广度误差，再按一定比例λ加上SSIM（结构相似性的误差）。
• 

4.22 自适应密度控制（Adaptive Control of Gaussians）

• 每100次迭代移除不透明度小于阈值的点：接近透明已经无用
• 重建不充分的区域往往会有较大的梯度：判断是否重建的依据为梯度，再更新点的位置时如果梯度过大说明该处的误差较大，需要修改的量较大，梯度超过阈值就会执行densify，第一排图像中沿梯度方向安置新的点；分为“欠重建”和“过重建”，根据方差区别，方差大，说明该3D高斯很大需要做分割，反之做克隆；
  – Under-reconstruction：clone，下图第一排，黑色线条为真是几何外形，它已不足以用一个高斯来拟合，所以克隆为2个，从而建模整个几何图案。
  – Over-reconstruction：split，下图第二排，当一个位置点太少，不足以完美覆盖一个复杂区域时，通过细胞分裂spli分成两个3D高斯来拟合。
• 周期性将不透明度重置为0用于去除floaters（floaters:漂浮的一些东西，不属于模型重建）；
• 周期性移除较大的高斯用于避免重叠。

点云密度的自适应控制使得系统能够从稀疏的质量不那么高的初始点云，甚至随机初始化的点云中拟合出较好的模型。

4.3 快速可微光栅化（Tile-based Rasterizer）

渲染方法仅依靠Splatting无法达到较高的实时渲染帧率，本文通过Tile-based Rasterizer

（1）、把整个图像划分为16*16个tiles，每个tile视锥内挑选可视的3D Gaussian；
（2）、每个视锥内只取执行度大于99%的高斯，并按深度排序；（
（3）、并行地在每个tile上splat；
（4）、有像素的不透明度达到饱和就停止对应线程；
（5）、反向传播误差时按tile对高斯进行索引。

取执行度大于99%的高斯后实例化为高斯对象，对象中包含所在tile的ID以及所在对应视域下的深度，通过这些信息对高斯对象进行排序；（将（2）中高斯按其到图像平面的深度值的排序顺序从近到远的tile上做splat，把splat留下的痕迹做堆叠累积直到不透明度饱和即为；每个tile都单独为一个线程块，所以可认为所有tile上的光栅化是并行运行的（光栅化指从堆叠的splat痕迹中去划分像素网格来生成像素值）

5、总结

• 从初始的SFM点云出发，以每个点为中心生成3D高斯；
  
• 然后用相机参数把点投影到图像平面上（Splatting）；
  
• 从Splatting的痕迹中进行Tile-base光栅化得到渲染图像，将渲染图像和GT图像求loss沿蓝色箭头反向传播；
  
• 根据传递到点上的梯度来决定是否需要对3D高斯进行克隆或分割，梯度同时也会传递到3D高斯来更新其中储存的位置（协方差矩阵、球谐函数、不透明度等参数）。
  
  核心：构建以协方差为主导的3D高斯点云，然后围绕3D高斯点云进行渲染和优化。