kmeans算法入门案例以聚类中心数的确定

目录

kmeans案例分析

kmeans具体流程

案例讲解 

生成的数据

代码

结果

聚类中心数的确定

肘部法

手肘法案例分析

生成的数据

代码 

结果

---

kmeans案例分析

kmeans具体流程

第一步：指定聚类类数k（文章后面会讲解k的选择方法）

第二步：选定初始化聚类中心。随机或指定k个对象，作为初始化聚类中心

第三步：得到初始化聚类结果。计算每个对象到k个聚类中心的距离，把每个对象分配给离它最近的聚类中心所代表的类别中，全部分配完毕即得到初始化聚类结果，聚类中心连同分配给它的对象作为一类

第四步：重新计算聚类中心。得到初始化聚类结果后，重新计算每类的类中心点（计算均值），得到新的聚类中心

第五步：迭代循环，得到最终聚类结果。重复第三步和第四步，直到满足迭代终止条件

案例讲解 

生成的数据

在本次实验中，我们先使用make_blobs（）这个函数设置中心点并且生成了五个簇。生成的图像如下

代码

import matplotlib.pyplot as plt
from sklearn.cluster import MiniBatchKMeans,KMeans
from sklearn import metrics
from sklearn.datasets._samples_generator import make_blobs

#生成数据集，其中X为二维数组，y为一维数组
X,y=make_blobs(n_samples=100,n_features=2,centers=[[-1,-1],[0,0],[1,1],[2,2],[4,4]],
               cluster_std=[0.4,0.2,0.2,0.2,0.2],random_state=9)


#生成数据散点图
#plt.scatter(X[:,0],X[:,1],marker='o')
# plt.show()

for index,k in enumerate((2,3,4,5)):
    # 将图像划分为两行两列的四个子图
    plt.subplot(2,2,index+1)

    #调用MiniBatchKMeans算法接口函数
    #n_clusters中心点的个数，batch_size确定MiniBatchKMeans的采样集的大小，random_state确定用于质心初始化的随机数生成
    #计算群集中心并预测每个样本的群集索引
    y_pred = MiniBatchKMeans(n_clusters=k,batch_size=200,random_state=9).fit_predict(X)

    #给聚类结果一个评分
    score = metrics.calinski_harabasz_score(X,y_pred)

    #绘制散点图，参数c为颜色
    plt.scatter(X[:,0],X[:,1],c=y_pred)
    #添加说明，前三个参数为x,y，字符串，transform为移动坐标轴，horizontalalignment为水平对其方式
    plt.text(.99,.01,('k=%d,score:%.2f' % (k,score)),transform=plt.gca().transAxes,
             size=10,horizontalalignment='right')

plt.show()

结果

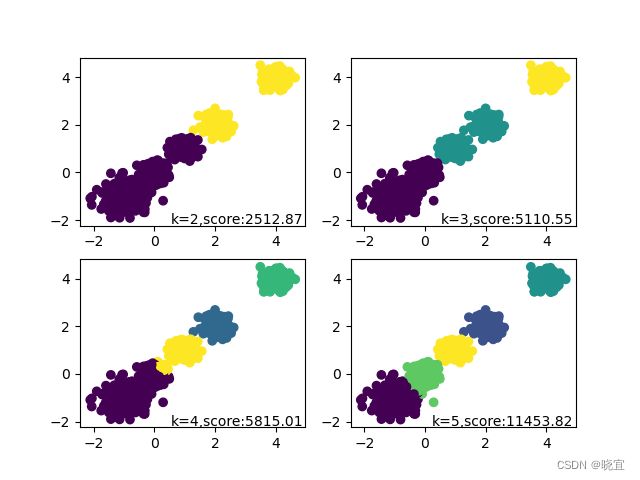
然后进入一个循环，设置不同的聚类中心点k的值，调用kmeans算法的一个接口进行分类，并且通过数据可视化的手段将结果表现在一张图片上。图片如下

聚类中心数的确定

肘部法

肘部法则对于K-means算法的K值确定起到指导作用

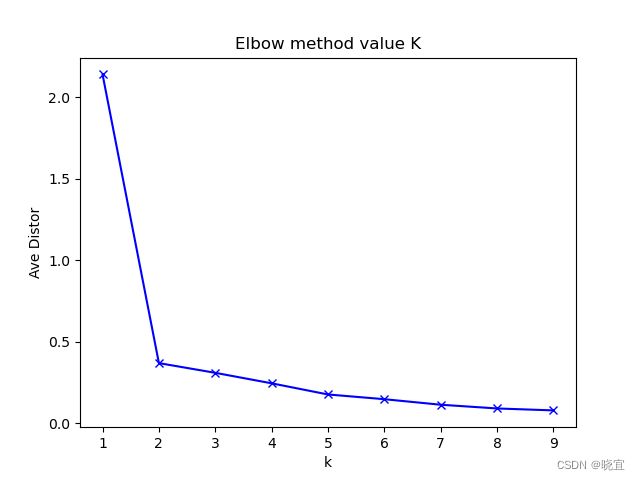
简单叙述一下肘部法则，由下图，y轴为平均畸变程度，x轴为k的取值，随着x的增加，SSE会随之降低，当下降幅度明显趋向于缓慢的时候，取该值为K的值。

 

手肘法案例分析

我们先生成一个分为两簇的列表，然后带入到算法当中，观察手肘法能否判断出k为2。

生成的数据

代码 

import numpy as np
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt

#生成数据集
#random.uniform()随机生成范围在（0.5，1.5）内的2*10的实数列表
cluster1 = np.random.uniform(0.5, 1.5, (2, 10))
cluster2 = np.random.uniform(3.5, 4.5, (2, 10))

#将两个两行十列的列表进行纵向叠加，生成一个20*2的列表
X = np.hstack((cluster1, cluster2)).T


#展示随机生成的数据
plt.figure()
plt.axis([0, 5, 0, 5])
plt.grid(True)
plt.plot(X[:,0],X[:,1],'k.');
plt.show()


#遍历k并且可视化
K = range(1, 10)
meandistortions = []
for k in K:
    kmeans = KMeans(n_clusters=k)
    kmeans.fit(X)
    #axis=0时会分别取每一列的最大值或最小值，axis=1时，会分别取每一行的最大值或最小值
    print(cdist(X, kmeans.cluster_centers_, 'euclidean'))
    meandistortions.append(sum(np.min(cdist(X, kmeans.cluster_centers_, 'euclidean'), axis=1)) / X.shape[0])

#用蓝色带拐点的线展示meandistortions的变化
plt.plot(K, meandistortions, 'bx-')
#设置x轴坐标
plt.xlabel('k')
#设置y轴坐标
# plt.ylabel('平均畸变程度',fontproperties=font)
plt.ylabel('Ave Distor')
#设置标题
plt.title('Elbow method value K');
plt.show()

结果