深度学习——第7章 项目实战：自己动手写一个神经网络模型

第7章 项目实战：自己动手写一个神经网络模型

目录

7.1 导入数据集

7.2 定义神经网络输入层、隐藏层、输出层神经元个数

7.3 网络参数W和b初始化

7.4 正向传播过程

7.5 损失函数

7.6 反向传播过程

7.7 网络参数更新

7.8 搭建整个神经网络模型

7.9 模型训练

7.10 模型预测

7.11 隐藏层神经元个数对分类效果的影响

上一课主要介绍了最简单的二层神经网络模型，详细推导其正向传播过程和反向传播过程，对整个神经网络的模型结构和数学理论推导过程有了清晰的认识和掌握。

本章将带大家使用Python搭建一个神经网络模型来解决实际的分类问题。

7.1 导入数据集

为了简化操作，我们直接构造一批数据集。

import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

r = np.random.randn(200)*0.8
x1 = np.linspace(-3, 1, 200)
x2 = np.linspace(-1, 3, 200)
y1 = x1*x1 + 2*x1 - 2 + r
y2 = -x2*x2 + 2*x2 + 2 + r

X = np.hstack(([x1, y1],[x2, y2]))                     # 输入样本 X，维度：2 x 400
Y = np.hstack((np.zeros((1,200)),np.ones((1,200))))    # 输出标签 Y

输入样本X的特征维度为2，样本个数为400，输出标签Y包含0和1类别各200个。

将数据集在二维平面上显示。

plt.scatter(X[0, :], X[1, :], c=np.squeeze(Y), s=40, cmap=plt.cm.Spectral);
plt.show()

从正负样本的分布来看，使用简单的逻辑回归进行分类效果肯定不会太好，因为数据集不是线性可分的。下面，我将带大家一步一步搭建一个简单的神经网络模型来解决这个分类问题。

7.2 定义神经网络输入层、隐藏层、输出层神经元个数

我们使用的简单神经网络，只包含一层隐藏层。首先，我们需要定义神经网络输入层、隐藏层、输出层的神经元个数。

m = X.shape[1]      # 样本个数
n_x = X.shape[0]    # 输入层神经元个数
n_h = 3             # 隐藏层神经元个数
n_y = Y.shape[0]    # 输出层神经元个数

7.3 网络参数W和b初始化

在上一篇中我们说过神经网络模型在开始训练时需要对各层权重系数W和常数项b进行初始化赋值。

初始化赋值时，b一般全部初始化为0即可，但是W不能全部初始化为0。

初始化代码如下：

W1 = np.random.randn(n_h,n_x)*0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_y,n_h)*0.01
b2 = np.zeros((n_y,1))
    
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
    
parameters = {"W1": W1,
              "b1": b1,
              "W2": W2,
              "b2": b2}

其中，assert语句对向量或者数组维度进行判断。如果与给定的维度不同，则程序在此处停止运行。assert的灵活使用可以帮助我们及时检查神经网络模型中参数的维度是否正确。

7.4 正向传播过程

正向传播过程，包含了$Z^{[1]}$，$A^{[1]}$，$Z^{[2]}$，$A^{[2]}$的计算，根据上一篇的详细推导结果：

$$Z^{[1]}=W^{[1]}X+b^{[1]}$$

$$A^{[1]}=g\left(Z^{[1]}\right)$$

$$Z^{[2]}=W^{[2]}{A}^{[1]}+b^{[2]}$$

$$A^{[2]}=g\left(Z^{[2]}\right)$$

其中，隐藏层的激活函数$g(\cdot )$选择使用tanh函数，输出层的激活函数$g(\cdot )$选择使用sigmoid函数。

定义 sigmoid 函数：

def sigmoid(x):
    """
    Compute the sigmoid of x
    """
    s = 1/(1+np.exp(-x))
    return s

定义正向传播过程：

def forward_propagation(X, parameters):

    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    Z1 = np.dot(W1,X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2,A1) + b2
    A2 = sigmoid(Z2)
    
    assert(A2.shape == (1, X.shape[1]))
    
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    
    return A2, cache

7.5 损失函数

$m$个样本的损失函数为：

$$J=-\frac{1}{m}\sum _{i=1}^m{y}^{(i)}log{\hat{y}}^{(i)}+(1-y^{(i)})log(1-{\hat{y}}^{(i)})$$

def compute_cost(A2, Y, parameters):
    
    m = Y.shape[1] # number of example

    # 计算交叉熵损失函数
    logprobs = np.multiply(np.log(A2),Y)+np.multiply(np.log(1-A2),(1-Y))
    cost = - 1/m * np.sum(logprobs)
    
    cost = np.squeeze(cost)     
    
    return cost

7.6 反向传播过程

反向传播过程需要计算损失函数$J$对各个变量$A^{[2]} $，$Z^{[2]} $，$W^{[2]}$，$b{[2]}$，$A^{[1]}$，$Z{[1]} $，$W^{[1]}$，$b{[1]} $的偏导数。根据上一篇的详细推导结果：

$$d{Z}^{[2]}=A^{[2]}-Y$$

$$d{W}^{[2]}=\frac{1}{m}d{Z}^{[2]}{A}^{[1]T}$$

$$d{b}^{[2]}=\frac{1}{m}np.sum(d{Z}^{[2]},axis=1)$$

$$d{Z}^{[1]}=W^{[2]T}d{Z}^{[2]}\ast g^{\prime }(Z^{[1]})$$

$$d{W}^{[1]}=\frac{1}{m}d{Z}^{[1]}{X}^T$$

$$d{b}^{[1]}=\frac{1}{m}np.sum(d{Z}^{[1]},axis=1)$$

反向传播函数定义为：

def backward_propagation(parameters, cache, X, Y):
    
    m = X.shape[1]
    
    W1 = parameters["W1"]
    W2 = parameters["W2"]
        
    A1 = cache["A1"]
    A2 = cache["A2"]
    
    # 反向求导
    dZ2 = A2 - Y
    dW2 = 1/m*np.dot(dZ2,A1.T)
    db2 = 1/m*np.sum(dZ2,axis=1,keepdims=True)
    dZ1 = np.dot(W2.T,dZ2)*(1 - np.power(A1, 2))
    dW1 = 1/m*np.dot(dZ1,X.T)
    db1 = 1/m*np.sum(dZ1,axis=1,keepdims=True)
    
    # 存储各个梯度值
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    
    return grads

7.7 网络参数更新

根据梯度下降算法，对网络参数W和b进行更新，并将新的网络参数存储在字典里。

def update_parameters(parameters, grads, learning_rate = 1.5):

    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]
    
    W1 = W1 - learning_rate*dW1
    b1 = b1 - learning_rate*db1
    W2 = W2 - learning_rate*dW2
    b2 = b2 - learning_rate*db2
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

7.8 搭建整个神经网络模型

各个模块已经写好，接下来要做的就是将各个模块组合起来，搭建整个神经网络模型。

def nn_model(X, Y, n_h = 3, num_iterations = 10000, print_cost=False):
    
    m = X.shape[1]      # 样本个数
    n_x = X.shape[0]    # 输入层神经元个数
    n_y = Y.shape[0]    # 输出层神经元个数
    
    W1 = np.random.randn(n_h,n_x)*0.01
    b1 = np.zeros((n_h,1))
    W2 = np.random.randn(n_y,n_h)*0.01
    b2 = np.zeros((n_y,1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}

    # 迭代训练
    J = []     # 存储损失函数
    for i in range(0, num_iterations):

        A2, cache = forward_propagation(X, parameters)            # 正向传播
        cost = compute_cost(A2, Y, parameters)                    # 计算损失函数
        grads = backward_propagation(parameters, cache, X, Y)     # 反向传播
        parameters = update_parameters(parameters, grads)         # 更新权重
        J.append(cost)
        # 每隔 1000 次训练，打印 cost
        if print_cost and i % 1000 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))

    return parameters

7.9 模型训练

接下来，就可以使用样本数据，对模型进行训练。

parameters = nn_model(X, Y, n_h = 3, num_iterations = 10000, print_cost=True)

输出结果：

Cost after iteration 0: 0.693201
Cost after iteration 1000: 0.061391
Cost after iteration 2000: 0.038519
Cost after iteration 3000: 0.039222
Cost after iteration 4000: 0.038911
Cost after iteration 5000: 0.038509
Cost after iteration 6000: 0.038056
Cost after iteration 7000: 0.037663
Cost after iteration 8000: 0.037349
Cost after iteration 9000: 0.037094

7.10 模型预测

模型搭建完毕之后，就可以使用训练好的模型对新样本进行预测。

def predict(parameters, X):
    
    A2, cache = forward_propagation(X, parameters)
    #predictions = A2 > 0.5
    predictions = np.zeros_like(A2)
    predictions[A2 > 0.5] = 1
    
    return predictions

y_pred = predict(parameters,X)
accuracy = np.mean(y_pred == Y)
print(accuracy)

输出结果：

0.9875

得到的预测准确率达到了98.25%。

最后，为了更直观地查看分类曲线和分类效果，我们绘制分类界限。

def plot_decision_boundary(model, X, y):

    x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
    y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
    h = 0.01

    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    Z = model(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(X[0, :], X[1, :], c=np.squeeze(y), cmap=plt.cm.Spectral)

plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary, hidden layers = 3")
plt.show()

输出结果：

7.11 隐藏层神经元个数对分类效果的影响

下面，分别设置隐藏层神经元个数n_h = 2、3、4、6，看看分类效果如何。

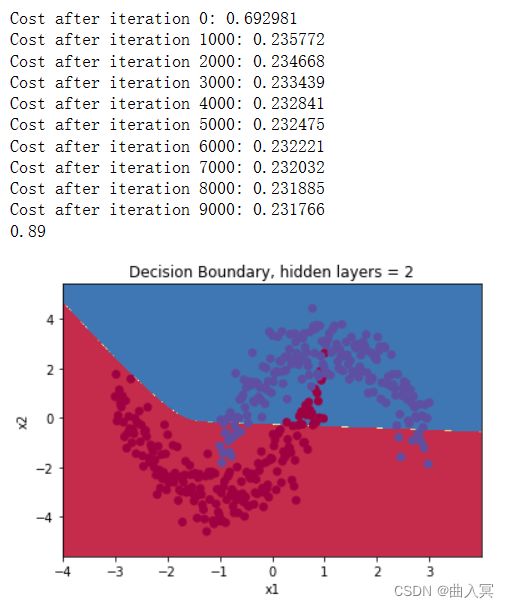
# n_h = 2
parameters = nn_model(X, Y, n_h = 2, num_iterations = 10000, print_cost=True)
y_pred = predict(parameters,X)
accuracy = np.mean(y_pred == Y)
print(accuracy)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary, hidden layers = 2")
plt.show()

输出结果：

当n_h = 2时，测得准确率为88.25%。

当n_h = 4时，测得准确率为98.5%。

可见，当n_4 = 4时，分类准确率最高。一般情况下，神经元个数越多，模型的分类准确率越高。但是，根据问题的复杂程度，一味地增加神经元个数不一定总会提高准确率，准确率可能会达到饱和状态。另外，神经元个数过多也容易造成过拟合。实际应用中，神经元个数一般可以通过交叉验证选择最佳个数。