爬虫案例—深圳租房数据的回归分析
公众号:尤而小屋
作者:Peter
编辑:Peter
大家好,我是Peter~
之前从网上爬取了一份深圳的租房数据,并且从统计分析和可视化的角度进行了分析。今天还是使用之前的数据进行数据分析和建模,以及模型的可解释性探索。本文的主要内容包含:
导入库
导入主要的库用于:数据处理、可视化、建模、特征可解释性等
数据基本信息
1、导入数据
2、数据形状和字段类型
下面是具体的特征解释:
# 下面是特征属性
name:小区名字
layout:几室几厅几卫
location:朝向
size:建筑面积
sizeInside:套内面积
zhuangxiu:装修方式
time:小区建成时间
zone:行政区
position:行政区的具体位置;比如宝安壹方中心,龙华民治等
way:出租方式,整租或者合租
# 最终的目标变量y
money:价格
3、查看数据的缺失值情况
使用的是df.isnull().sum()来查看:在time字段中存在6个缺失值
4、缺失值填充
由于缺失量比较少,直接在网上搜索到相应的时间进行了人工填充:先定位缺失值的位置,再进行填充
字段预处理
name
小区的姓名name直接删除
df.drop("name",axis=1,inplace=True)
layout
layout分成3个具体的属性:室、厅、卫
特殊情况:当layout为"商铺"时,直接删除~
使用正则解析出室厅卫:
df1 = df["layout"].str.extract(r'(?P\d)室(?P\d)厅(?P\d)卫' )
# 合并到原数据
df = pd.concat([df1,df],axis=1)
# 删除layout
df.drop("layout",axis=1,inplace=True)
# layout=商铺正则解析为NaN,直接删除
df.dropna(subset=["shi","ting","wei"],inplace=True)
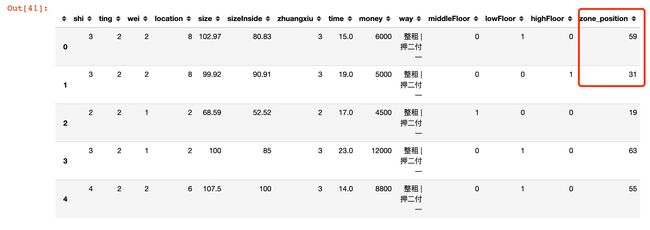
df.head()
location
不同朝向的房子数量:
df["location"].value_counts()
朝南 552
朝南北 284
朝北 241
朝东南 241
朝西南 174
朝西北 142
朝东北 140
朝东 132
朝西 92
朝东西 2
Name: location, dtype: int64
# 小提琴图
fig = px.violin(df,y="money",color="location")
fig.show()
小结:可以看到,在朝南北、朝南、朝北的房子数量比较多,而且整体的价格分布更为广泛。
对不同朝向的房子实施硬编码:
# 自定义的顺序:根据朝向和价格的关系图(上面)
location = ["朝东西","朝东北","朝西","朝西北","朝东","朝西南","朝东南","朝南","朝北","朝南北"]
location_dict = {}
for n, i in enumerate(location):
location_dict[i] = n+1 # 保证序号从1开始
df["location"] = df["location"].map(location_dict)
df.head()
size和sizeInside
建筑面积和套内面积提取出数值部分,提供两种方法:
# 1、通过切割的方式来提取
df["size"] = df["size"].apply(lambda x: x.split("面积")[1].split("㎡")[0])
# 2、使用正则的方式提取
df["sizeInside"] = df["sizeInside"].str.extract(r'面积(?P[\d.]+)' )
df.head()
zhuangxiu
df["zhuangxiu"].value_counts()
精装 1172
普装 747
豪装 62
毛坯 19
Name: zhuangxiu, dtype: int64
主观意义上的思路:毛坯的等级最低,豪装最高。下面实施硬编码过程:
# 硬编码
zhuangxiu = {"毛坯":1,"普装":2, "精装":3, "豪装":4}
zhuangxiu
{'毛坯': 1, '普装': 2, '精装': 3, '豪装': 4}
df["zhuangxiu"] = df["zhuangxiu"].map(zhuangxiu)
df.head()
numberFloor
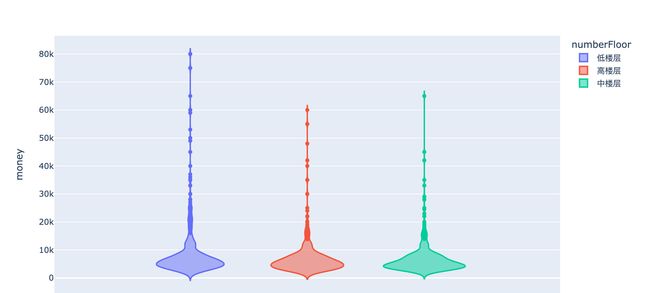
中低高楼层和价格money之间的关系
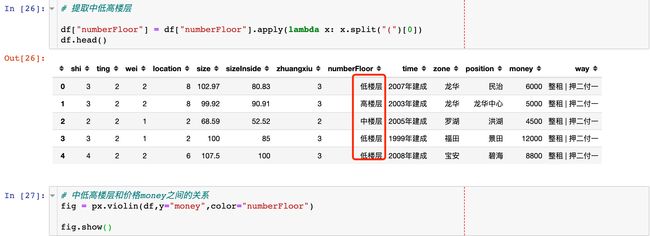
# 提取中低高楼层
df["numberFloor"] = df["numberFloor"].apply(lambda x: x.split("(")[0])
df.head()
小结:中低高3个楼层在房租上面的影响稍小。直接考虑独热编码的方式:
df = (df.join(pd.get_dummies(df["numberFloor"]))
.rename(columns={"中楼层":"middleFloor",
"低楼层":"lowFloor",
"高楼层":"highFloor"}))
df.head()
df.drop("numberFloor",axis=1,inplace=True) # 删除原字段
time
房子的建成时间处理:
df["time"].value_counts()
# 部分结果
2003年建成 133
2005年建成 120
2006年建成 114
2004年建成 111
2010年建成 104
......
2019年 3 # 人工填充的时间
2022年建成 2
1983年建成 1
2003年 1
2020年 1
2004年 1
Name: time, dtype: int64
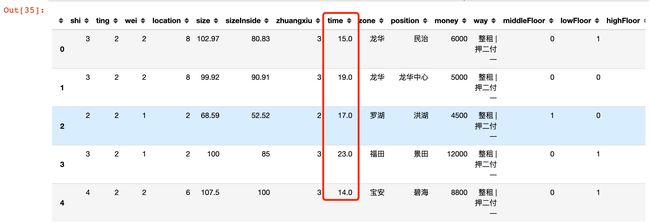
提取时间年份:
df["time"] = df["time"].str.extract(r'(?P)
# time转成数值型
df["time"] = df["time"].astype("float")
# 建成时间和当前的差距
df["time"] = 2022 - df["time"]
df.head()
zone+position
行政区域和地理位置的合并处理
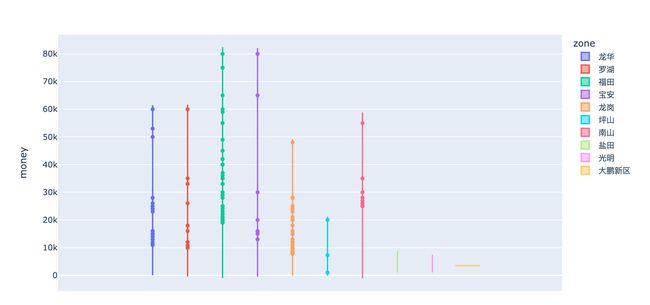
df["zone"].value_counts()
龙岗 548
福田 532
龙华 293
南山 218
宝安 173
罗湖 167
光明 32
坪山 31
盐田 5
大鹏新区 1
Name: zone, dtype: int64
# 行政区和价格的关系
fig = px.violin(df,y="money",color="zone")
fig.show()
# 合并字段
df["zone_position"] = df["zone"] + "_" + df["position"]
df.head()
不同行政区域不同地理位置下的价格均值统计:
zone_position_mean =
(df.groupby("zone_position")["money"].mean()
.reset_index()
.sort_values("money",ascending=False,ignore_index=True))
zone_position_mean
根据合并的zone_position_mean数据框中的money 来进行硬编码:福田_车公庙 是最高位
zone_position = zone_position_mean["zone_position"].tolist()[::-1]
zone_position_dict = {}
for n, i in enumerate(zone_position):
zone_position_dict[i] = n+1
df["zone_position"] = df["zone_position"].map(zone_position_dict)
# 删除原字段
df.drop(["zone","position"],axis=1,inplace=True)
df.head()
way
出租方式和价格的关系探索:
fig = px.violin(df,y="money",color="way")
fig.show()
从way的取值来看:大部分的房子是愿意整租的,而且押一付一和押二付一最为普遍。提取出“整租”和“合租”两种方式:
df["way"] = df["way"].apply(lambda x: x.split(" ")[0])
# 编码
df["way"] = df["way"].map({"整租":1,"合租":0})
df
终于:算是得到一份比较符合建模的数据
样本不均衡
我们查看way字段下的数据情况:明显way=1的取值情况是远远大于way=0。
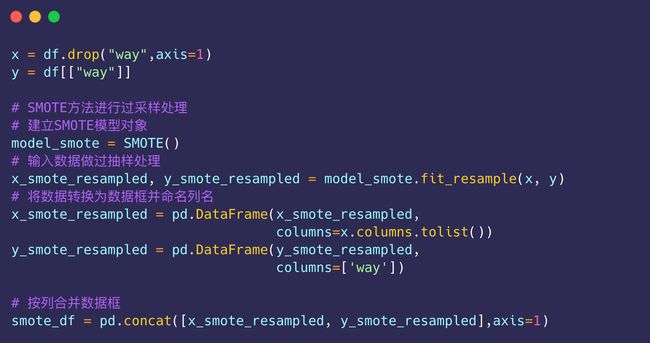
解决方法:使用SMOTE算法来解决解决way=0过少的问题。
解决之后的way=1和way=0的样本相同:
字段异常处理
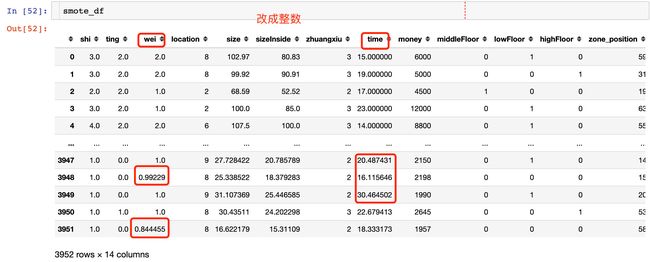
1、填充样本后发现某些应该是整数,却出现了小数,比如:wei和time等
cols = ["shi","ting","wei","time"]
for i in cols:
smote_df[i] = smote_df[i].apply(lambda x: round(x))
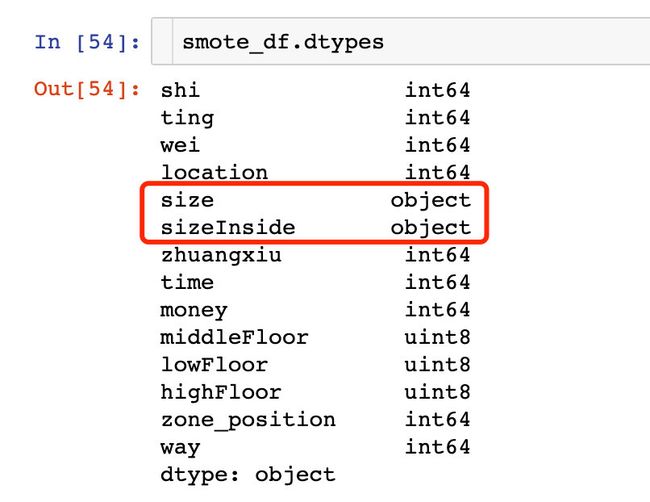
2、类型转化
# 转变数据类型
smote_df["size"] = smote_df["size"].astype(float)
smote_df["sizeInside"] = smote_df["sizeInside"].astype(float)
相关性分析
相关系数
针对上面得到的smote_df数据进行下面的相关性分析:
# 保存了再读取
# smote_df.to_csv("data_new.csv",index=False)
df = pd.read_csv("data_new.csv")
1、相关性
能够直观看到money因变量和size与sizeInside相关性很强
corr = df.corr()
f,ax=plt.subplots(figsize=(12,6))
sns.heatmap(corr,vmax=0.8,square=True,fmt='.2f', cmap='PuBu_r')
plt.show()
相关系数排序
单个属性和money之间的相关性大小排序,可以看到:size(房子面积)、sizeInsize(套内面积)和wei(卫)的相关型比较强。
单纯地从相关系数得到的结论,还是有待考证~
自变量和因变量关系
上面举出3个字段和money之间的相关性,在最右侧:
- size和sizeInside相对集中的时候,money高频出现0-25000之间
- 在不同的money取值情况,wei字段的取值集中在1-4之间
建模
特征归一化
下面是针对数据的归一化过程,采用的MinMaxScaler方法:
X = df.drop("money",axis=1)
y = df[["money"]]
# 实例化
mm = MinMaxScaler()
data = mm.fit_transform(X)
# 归一化后的数据
X = pd.DataFrame(data,columns=X.columns.tolist())
X.head()
数据集切分
按照训练集:测试集 = 8:2的比例进行数据集的划分:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size=0.2, # 比例
random_state=4 # 随机状态
)
特征选择
在前面的工作我们从相关系数和因变量的相关性大小进行了比较,发现:Size、sizeInside和wei是比较相关的系数。
下面是从使用mutual_info_classif来查看每个特征的重要性:
from sklearn.feature_selection import mutual_info_classif
imp = pd.DataFrame(mutual_info_classif(X,y),
index=X.columns)
imp.columns=['importance']
imp.sort_values(by='importance',ascending=False)
我们发现:shi、wei、zhuangxiu、size都是比较重要的特征
评价指标
引入多种回归模型:
# 线性回归
from sklearn.linear_model import LinearRegression
# 决策树回归
from sklearn.tree import DecisionTreeRegressor
# 梯度提升回归,随机森林回归
from sklearn.ensemble import GradientBoostingRegressor,RandomForestRegressor
不同模型效果
重点关注模型的r2值
1、线性回归-LinearRegression
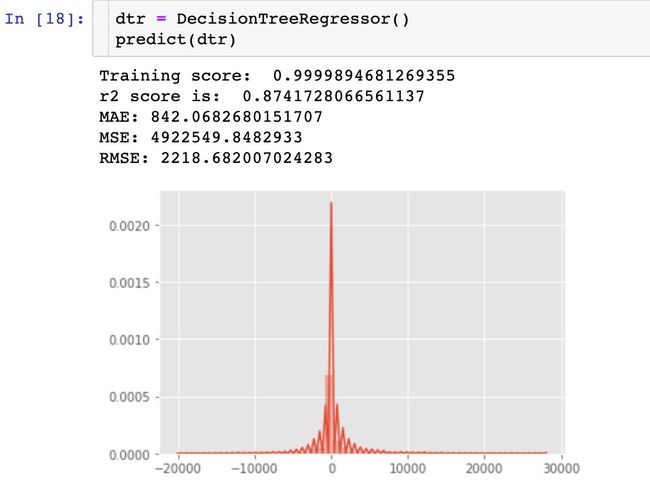
2、决策树回归-DecisionTreeRegressor
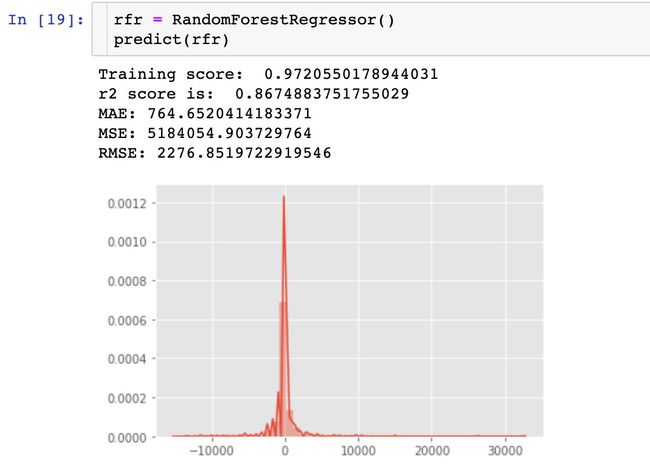
3、随机森林回归-RandomForestRegressor
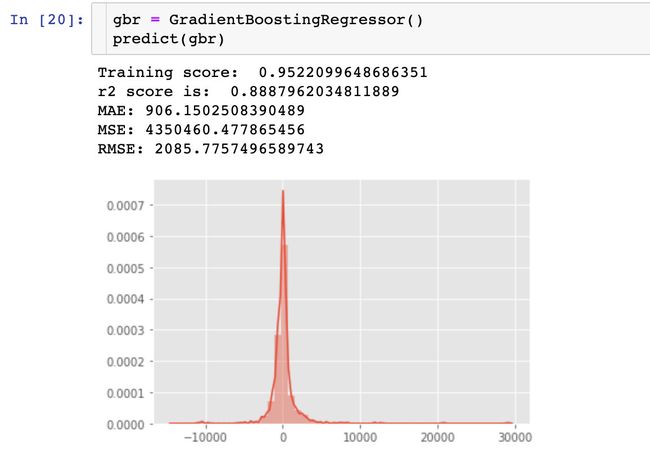
4、梯度提升回归-GradientBoostingRegressor
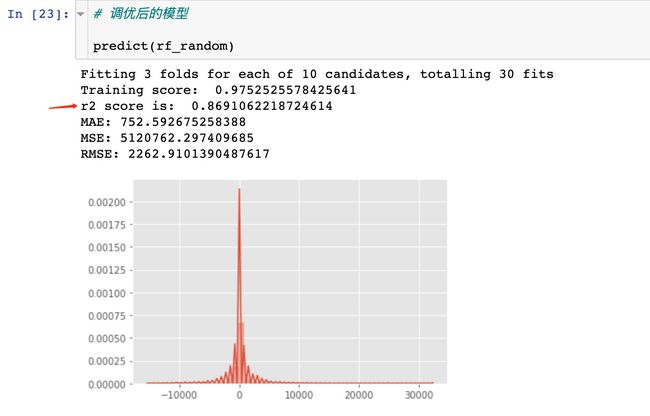
通过3种回归模型的r2得分比较:GradientBoostingRegressor > DecisionTreeRegressor > RandomForestRegressor > LinearRegression
模型可解释分析
为了更好理解机器学习模型的输出,下面使用SHAP库来探索调参后随机森林模型的可解释性。通过pip install shap即可安装
随机森林调参
进行fit拟合之后便得到了最优的参数组合:
rf_random.best_params_
# 结果
{'n_estimators': 120, 'max_features': 'auto', 'max_depth': 20}
调参后随机森林模型的r2系数略优于调参前:
建立最佳参数下的模型:
rf_random = RandomForestRegressor(
n_estimators=180,
max_features="auto",
max_depth=10)
rf_random.fit(X_train, y_train)
计算shap_values
SHAP value最大的优势是SHAP能对于反映出每一个样本中的特征的影响力,而且还能够表现出影响的正负性。
在SHAP中进行模型解释需要先创建一个explainer,SHAP支持很多类型的explainer
# 1、传入调优模型rf_random创建explainer
explainer = shap.TreeExplainer(rf_random)
# 2、计算shap值
shap_values = explainer.shap_values(X_test)
shap_values
均值对比
1、通过模型预测得到的均值求解
# y的预测值和真实值比较
y_pred = rf_random.predict(X_test)
# 预测值
y_test["pred"] = y_pred
# money部分是真实值
y_test.head()
其中:money-真实值,pred-随机森林模型的预测值。得到的均值为:
# 真实的平均值
y_test["pred"].mean()
5614.137953764154
2、通过SHAP得到的基准值base_value
# shap得到的基准值
y_base = explainer.expected_value
y_base
array([5487.93357763])
整体特征重要性
取出每个特征的shap值的绝对值的平均值作为该特征的重要性,得到水平的条形图:
shap.summary_plot(shap_values,
X_test,
plot_type="bar")
shap.summary_plot(shap_values, X_test)
可以看到,通过shap值来看:
- size面积、zone_position区域位置、shi房间数 的重要性才是最靠前的,这个结果可以和相关系数的大小进行对比
- 前5个特征中,蓝点主要还是集中在SHAP值小于0的区域
单个样本的SHAP值
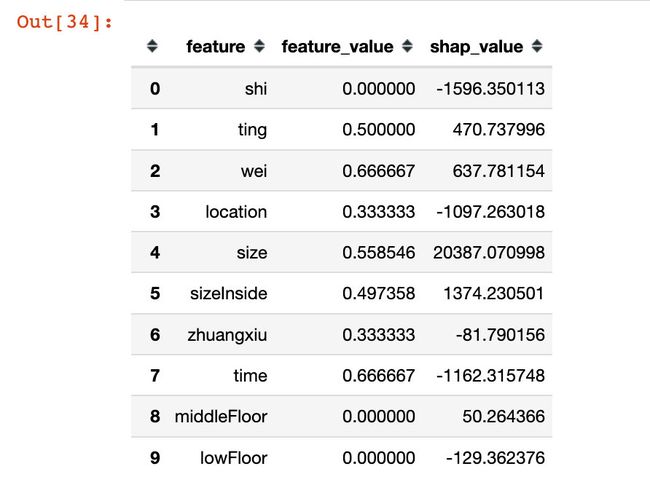
从数据中随机抽查一条样本查看shap值:
i=18
df0 = pd.DataFrame()
df0['feature'] = X_test.columns.tolist()
df0['feature_value'] = X_test.iloc[i].values
df0['shap_value'] = shap_values[i]
df0.head(10)
- 第一列是特征名称
- 第二列是特征的具体数值
- 第三列是各个特征在该样本中对应的SHAP值
注意:一个样本中各特征 SHAP 值的和加上基线值应该等于该样本的预测值
单条样本的特征可视化:
# 可视化
shap.initjs()
shap.force_plot(
explainer.expected_value,
shap_values[i],
X_test.iloc[i])
红色表示higher部分:表明针对这条数据,zone_position和size是重要的特征。下面是换了另一个样本的结果:
不同的样本具有不同的重要属性
部分依赖图-Partial Dependence Plot
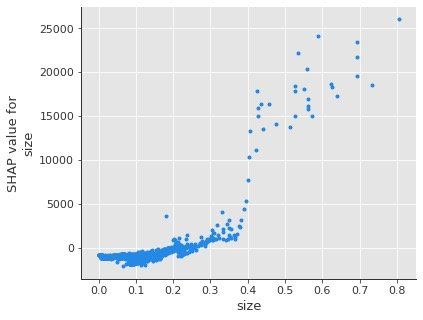
1、单个变量的影响
shap.dependence_plot('size',
shap_values,
X_test,
interaction_index=None,
show=False)
通过图形我们观察到:size的取值在0.4以下,size的shap都是相对平和。一旦size达到一定值,对房租价格的拉升作用相当明显。
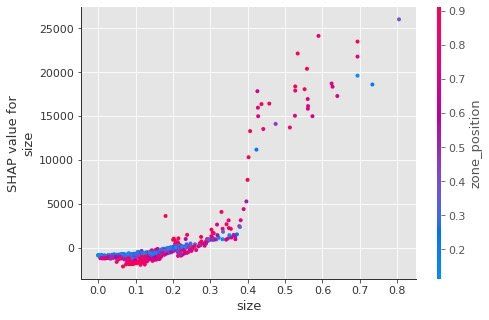
2、两个变量的交互式影响
SHAP同样能够查看两个变量的交互式影响,比如size和zone_position。
shap.dependence_plot(
'size',
shap_values,
X_test,
interaction_index='zone_position', # 指定
show=False)
当指定了interaction_index 的取值情况,我们不仅能够观察到size和房租的关系,还可以看到size和zone_position之间存在的关系:size在分界点(大致在0.4)前后,one_position的相应都比较大(红色),这同时表明zone_position是一个重要性高的特征~