风控实战-卡方分箱计算IV值(含代码)
统计学,风控建模经常遇到卡方分箱算法ChiMerge。卡方分箱在金融信贷风控领域是逻辑回归评分卡的核心,让分箱具有统计学意义(单调性)。卡方分箱在生物医药领域可以比较两种药物或两组病人是否具有显著区别。
01
卡方检验算法介绍
卡方检验(Chi-Square Test)是一种统计学上的检验方法,用于评估两个类别变量之间的独立性。它基于样本数据来测试观察值与预期值之间的差异是否足够大,以至于能够推断变量之间存在关联,而不是偶然发生的。
1. 卡方检验的类型
1.卡方拟合度检验(Goodness of Fit Test):
- 用于检验一个样本的分布是否符合预期的理论分布。
2.卡方独立性检验:
- 用于检验两个分类变量是否相互独立。
2. 卡方检验的基本步骤
1.构建列联表(Contingency Table):
- 所有观察值被分配到一个由两个类别变量定义的表中,表的每个单元格包含对应分类组合的频数。
2. 计算期望频数:
- 根据每个类别在其边际分布中的比例,计算出每个单元格的期望频数。
3. 计算卡方统计量:
- 使用下述公式计算卡方统计量:(chi^2 = sum\frac{(O_i - E_i)^2}{E_i})
其中,(O_i) 是观察频数,(E_i) 是期望频数。
4. 确定自由度(Degree of Freedom,df):
- 通常,自由度由表的行数和列数决定:(df = (行数 - 1) \times (列数 - 1))
5. 比较卡方统计量与临界值或使用p-value:
- 通过自由度和显著性水平查卡方分布表,找到对应的临界值比较,或直接计算p-value。
6. 作出结论:
- 如果卡方统计量大于临界值或p-value小于显著性水平,拒绝原假设,表明变量之间不独立。
3. 卡方检验的应用
- 频数比较:检验实际数据与预期数据是否有显著性差异。
- 特征选择:在机器学习中,用来选择与目标变量相关性显著的特征。
- 变量关联度分析:在市场研究、生物统计学等领域评估不同群体之间的关系。
#注意点#:
- 卡方检验要求观察频数足够大,一般认为单个单元格的期望频数应不小于5。
- 它是一个非参数检验,不需要关于数据分布的假设。
- 它只能用于分类数据,而不能用于连续数据,除非连续数据被分组为类别。
在实践中,卡方检验被广泛应用于不同领域中的假设检验,尤其是用于评估两个类别变量之间的相关性。
02
卡方分箱逻辑
ChiMerge卡方分箱算法由Kerber于1992提出。
它主要包括两个阶段:初始化阶段和自底向上的合并阶段。
卡方分箱(Chi-Square Binning)是一种在统计学中常用于分析两个分类变量之间关联性的方法,它在信用评分模型等金融风控领域中被用于将连续变量离散化。卡方分箱的目的是找到最佳的离散化方式,简化模型并提高其解释能力。
1. 卡方分箱的基本步骤包括
1.数据排序:
- 将需要分箱的连续变量按照从小到大的顺序进行排序。
2.初步分箱:
- 将连续变量划分为较多的小区间,每个小区间可以看做是初始的“箱子”,例如等频分成20箱。
3.计算每个箱子的卡方值:
- 对于每一对相邻的箱子,计算其卡方值。卡方值是基于每个箱子内观测频数(如好客户和坏客户数量)和期望频数的差异计算出的统计量。
- 期望频数是基于假设变量与目标变量独立时预期的频数。
- 卡方值越高,说明两个箱子的区分度越好。
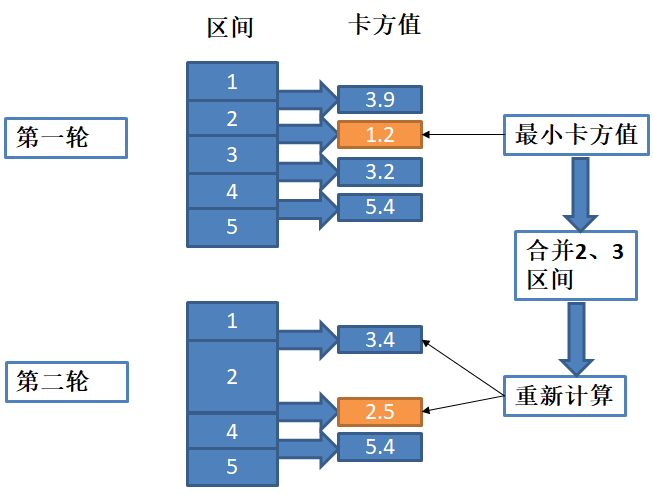
4.合并箱子:
- 从卡方值最小的一对箱子开始合并,因为小的卡方值意味着这两个箱子的区分能力最弱。
- 在每次合并后,重新计算所有相邻箱子的卡方值。
5.停止条件:
- 当箱子数达到预设的目标个数,或者所有的卡方值都高于某个统计学意义水平的阈值时,停止合并。
- 统计学意义水平通常通过卡方分布和自由度来确定,自由度通常是(箱子数-1)。
6.基于IV评估分箱效果:
- 评估每个箱子的区分能力,可能还会基于业务知识、单调性对分箱结果进行微调。
2. 卡方分箱的优点
◆ 逻辑简单:卡方分箱方法直观且易于理解和实现。
◆ 自动化:可以编程自动执行,而不需要人为判断。
◆ 稳健性:卡方分箱对异常值具有一定的稳健性。
3. 卡方分箱的缺点
◆数据依赖性:卡方分箱的结果很大程度上依赖于数据的分布情况,如果数据集中存在偏差,可能会影响分箱结果的有效性。
◆过度拟合:如果箱子数过多,可能会导致模型在训练集上过度拟合。
卡方分箱方法在实践中广受好评,尤其是在变量的预处理阶段,能够帮助识别和把握变量的分布特征和区分能力。在实际操作中,卡方分箱也需要结合业务知识和模型目标来适度调整。
03
卡方分箱实战
在卡方分箱的实际案例中,我们可以对一组客户的年龄数据进行分箱处理,并根据客户是好客户还是坏客户来评估每个箱子的风险。以下是一个卡方分箱的Python代码示例,它使用了pandas和scipy库来实现分箱过程。
1. 卡方分箱案例一(年龄变量)
import pandas as pd
from scipy.stats import chi2_contingency
# 假设我们有以下数据集,包含客户的年龄和好坏客户标签(1代表好客户,0代表坏客户)
data = {
'年龄': [22, 25, 30, 32, 35, 40, 45, 50, 55, 60],
'好坏客户': [1, 1, 1, 0, 0, 1, 0, 0, 1, 0]
}
df = pd.DataFrame(data)
# 初始分箱,这里我们以10年一个箱子为例进行初始分箱
df['年龄分箱'] = pd.cut(df['年龄'], bins=range(20, 70, 10), right=False)
# 计算每个箱子中好坏客户的数量
cross_tab = pd.crosstab(df['年龄分箱'], df['好坏客户'])
print(f"初始分箱的列联表:\n{cross_tab}\n")
# 定义函数,用于合并最小卡方值对应的箱子
def merge_chi2_smallest_bin(cross_tab):
min_chi2 = float('inf')
min_chi2_idx = -1
# 计算相邻箱子之间的卡方值
for i in range(len(cross_tab) - 1):
chi2, p, dof, ex = chi2_contingency([cross_tab.iloc[i], cross_tab.iloc[i + 1]])
if chi2 < min_chi2:
min_chi2 = chi2
min_chi2_idx = i
# 合并卡方值最小的一对箱子
new_row = cross_tab.iloc[min_chi2_idx] + cross_tab.iloc[min_chi2_idx + 1]
new_cross_tab = cross_tab.drop(cross_tab.index[min_chi2_idx:min_chi2_idx + 2])
new_cross_tab = new_cross_tab.append(new_row, ignore_index=True)
return new_cross_tab.sort_index().reset_index(drop=True)
# 持续合并箱子直到满足某个停止条件,这里我们设定最小箱数为3个
while len(cross_tab) > 3:
cross_tab = merge_chi2_smallest_bin(cross_tab)
# 输出合并后的列联表
print(f"合并后的列联表:\n{cross_tab}\n")
# 根据合并后的列联表重新分配年龄分箱
bins = [20] + list(cross_tab['年龄分箱'].cat.categories[1:-1]) + [70]
df['年龄分箱'] = pd.cut(df['年龄'], bins=bins, right=False)
print(f"最终年龄分箱结果:\n{df[['年龄', '年龄分箱']]}")上述代码执行了以下操作:
-
创建一个模拟数据集,包含年龄和好坏客户标签。
-
初始分箱,这里以10年为一个箱子进行初始划分。
-
计算每个箱子中好坏客户的数量,构建列联表。
-
定义一个函数
merge_chi2_smallest_bin来合并具有最小卡方值的相邻箱子。 -
循环合并箱子,直到箱子数量降到3个为止(或者你可以定义其他停止条件)。
-
根据最终的箱子,重新划分年龄数据。