Day31 贪心算法 part01 理论基础 455.分发饼干 376.摆动序列 53.最大子序和

贪心算法 part01 理论基础 455.分发饼干 376.摆动序列 53.最大子序和

理论基础（转载自代码随想录）

什么是贪心

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

这么说有点抽象，来举一个例子：

例如，有一堆钞票，你可以拿走十张，如果想达到最大的金额，你要怎么拿？

指定每次拿最大的，最终结果就是拿走最大数额的钱。

每次拿最大的就是局部最优，最后拿走最大数额的钱就是推出全局最优。

再举一个例子如果是 有一堆盒子，你有一个背包体积为n，如何把背包尽可能装满，如果还每次选最大的盒子，就不行了。这时候就需要动态规划。动态规划的问题在下一个系列会详细讲解。

贪心的套路（什么时候用贪心）

很多同学做贪心的题目的时候，想不出来是贪心，想知道有没有什么套路可以一看就看出来是贪心。

说实话贪心算法并没有固定的套路。

所以唯一的难点就是如何通过局部最优，推出整体最优。

那么如何能看出局部最优是否能推出整体最优呢？有没有什么固定策略或者套路呢？

不好意思，也没有！ 靠自己手动模拟，如果模拟可行，就可以试一试贪心策略，如果不可行，可能需要动态规划。

有同学问了如何验证可不可以用贪心算法呢？

最好用的策略就是举反例，如果想不到反例，那么就试一试贪心吧。

可有有同学认为手动模拟，举例子得出的结论不靠谱，想要严格的数学证明。

一般数学证明有如下两种方法：

• 数学归纳法
• 反证法

看教课书上讲解贪心可以是一堆公式，估计大家连看都不想看，所以数学证明就不在我要讲解的范围内了，大家感兴趣可以自行查找资料。

面试中基本不会让面试者现场证明贪心的合理性，代码写出来跑过测试用例即可，或者自己能自圆其说理由就行了。

举一个不太恰当的例子：我要用一下1+1 = 2，但我要先证明1+1 为什么等于2。严谨是严谨了，但没必要。

虽然这个例子很极端，但可以表达这么个意思：刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。

例如刚刚举的拿钞票的例子，就是模拟一下每次拿做大的，最后就能拿到最多的钱，这还要数学证明的话，其实就不在算法面试的范围内了，可以看看专业的数学书籍！

所以这也是为什么很多同学通过（accept）了贪心的题目，但都不知道自己用了贪心算法，因为贪心有时候就是常识性的推导，所以会认为本应该就这么做！

那么刷题的时候什么时候真的需要数学推导呢？

例如这道题目：链表：环找到了，那入口呢？ (opens new window)，这道题不用数学推导一下，就找不出环的起始位置，想试一下就不知道怎么试，这种题目确实需要数学简单推导一下。

贪心一般解题步骤

贪心算法一般分为如下四步：

• 将问题分解为若干个子问题
• 找出适合的贪心策略
• 求解每一个子问题的最优解
• 将局部最优解堆叠成全局最优解

这个四步其实过于理论化了，我们平时在做贪心类的题目 很难去按照这四步去思考，真是有点“鸡肋”。

做题的时候，只要想清楚 局部最优 是什么，如果推导出全局最优，其实就够了。

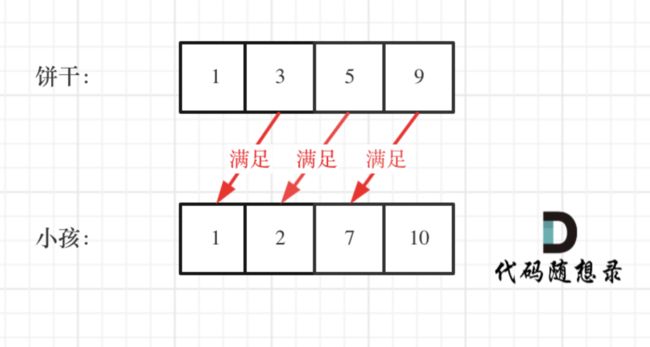
455. 分发饼干

思路:

这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。

可以尝试使用贪心策略，先将饼干数组和小孩数组排序。

然后从后向前遍历小孩数组，用大饼干优先满足胃口大的，并统计满足小孩数量。

如图：

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(),g.end()); //胃口
        sort(s.begin(),s.end()); //饼干
        int index = s.size()-1; //饼干最大尺寸
        int result = 0;//存放结果
        for(int i =g.size()-1; i>=0;i--){ //遍历胃口
            if(index>=0&&s[index]>=g[i]){
                index--;
                result++;
            }
        } 
        return result;
    }
};

376. 摆动序列

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        if(nums.size()<=1) return nums.size();
        int prediff = 0;
        int curdiff = 0;
        int result = 1;
        for(int i = 0; i<nums.size()-1;i++){
            curdiff = nums[i+1] - nums[i];
            if((prediff>=0&&curdiff<0) || (prediff<=0&&curdiff>0)){
                result++;
                prediff = curdiff;
            }
        }
        return result;
    }
};

53. 最大子数组和

注释掉的是贪心算法，下面的是dp动态规划

class Solution {
public:
    int maxSubArray(vector<int>& nums) { //贪心算法
//         int result = INT32_MIN;
//         int count = 0;
//         for(int j = 0; j
//             count += nums[j];
//             result = count > result ? count : result;
//             count = count < 0 ? 0 :count;
//         }
//  return result;
    vector<int> dp(nums.size());//dp动态规划
    if (dp.size()==0) return 0;

    dp[0] = nums[0];
    int result = dp[0];
    for(int i = 1; i<nums.size();i++){
        dp[i] = max(dp[i-1]+nums[i],nums[i]);
        result = (result>dp[i])?result:dp[i];
    }
    return result;
    }
};