数据结构——二叉树的遍历与应用
目录
一.前言
二. 二叉树链式结构的实现
2.1 前置说明
2.2 二叉树的遍历
2.2.1 前序、中序以及后序遍历
前序遍历:
中序遍历递归图:
后序遍历:
2.3节点个数
2.4叶子节点个数
2.5第K层的节点个数
2.6 二叉树查找值为x的节点
2.7 二叉树的销毁
三.结语
一.前言
大家好久不见,放寒假了咱得还债了,争取这个寒假能把c++篇写一大半!码字不易,希望大家多多支持我呀!(三连+关注,你是我滴神!)
二. 二叉树链式结构的实现
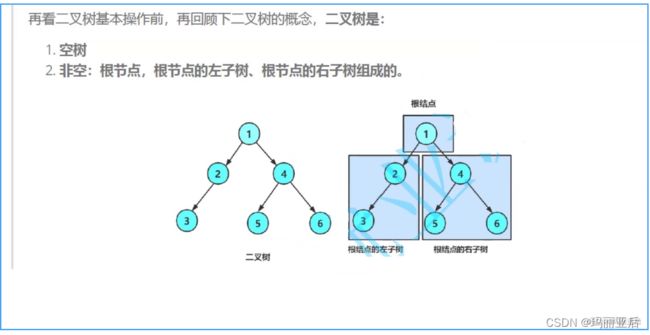
2.1 前置说明
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。为了方便大家理解,这里我先采用手动创建一棵简单的二叉树来快速进行操作学习,等二叉树结构完结得差不多我们再来研究二叉树真正的创建方式。
//搭建二叉树结构 typedef struct BinaryTreeNode { struct BinaryTreeNode* left; struct BinaryTreeNode* right; int val; }BTNode; //创造节点 BTNode* BuyNode(int x) { BTNode* node = (BTNode*)malloc(sizeof(BTNode)); if (node == NULL) { perror("node faild"); exit(-1); } node->val = x; node->left = NULL; node->right = NULL; return node; } int main() { //手动构建节点 BTNode* node1 = BuyNode(1); BTNode* node2 = BuyNode(2); BTNode* node3 = BuyNode(3); BTNode* node4 = BuyNode(4); BTNode* node5 = BuyNode(5); BTNode* node6 = BuyNode(6); //开始链接 node1->left = node2; node1->right = node4; node2->left = node3; node4->left = node5; node4->right = node6; }
2.2 二叉树的遍历
2.2.1 前序、中序以及后序遍历
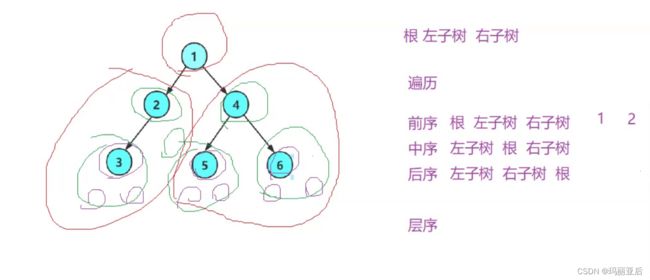
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最主要的运算之一,也是二叉树上进行其他运算的基础。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历——访问根结点的操作发生在遍历其左右子树之中。
- 后序遍历——访问根结点的操作发生在遍历其左右子树之后。
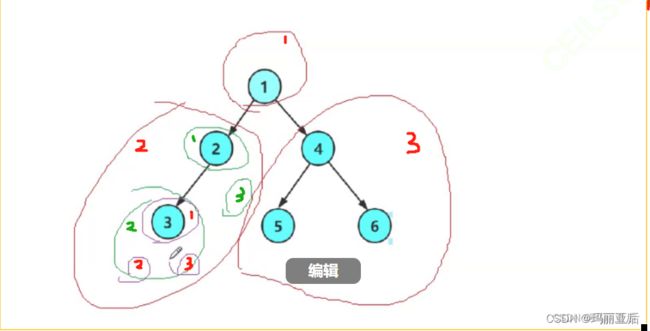
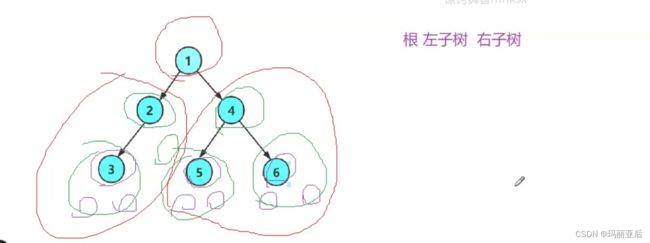
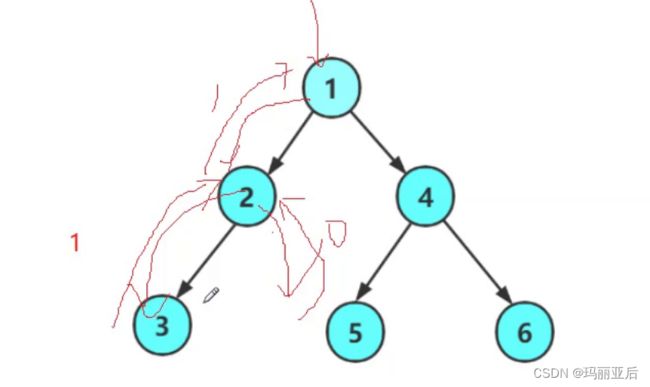
以后遇到二叉树就要拆解为根、左子树、右子树。每一个结点都要这样
对前序而言,如果我们通过顺序先访问1,到了访问2时,也要把2拆解为根(2),左子树(3),右子树(空)。先去访问左子树3,而3拆为根时左右子树都是null。然后再去访问根为2时的右子树(空)
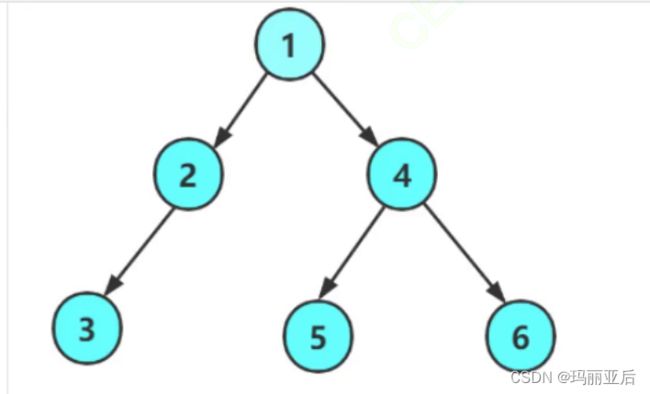
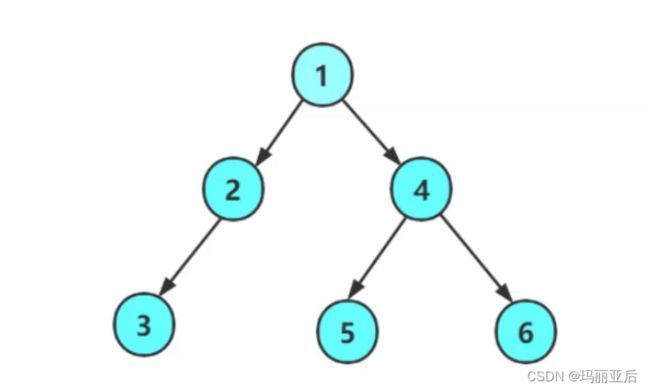
我们先来按照这个形状来构建节点并链接起来
//搭建二叉树结构
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
int val;
}BTNode;
//创造节点
BTNode* BuyNode(int x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("node faild");
exit(-1);
}
node->val = x;
node->left = NULL;
node->right = NULL;
return node;
}
int main()
{
//手动构建节点
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
//开始链接
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
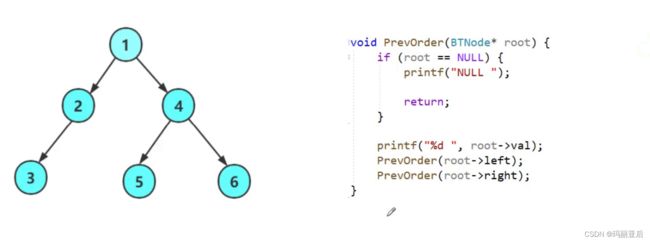
}前序遍历:
涉及到子问题嵌套子问题,是深入了解二叉树遍历分治(递归)的开始~
//前序遍历
void PrevOrder(BTNode* root)
{
//当二叉树无根时
if (root == NULL)
{
printf("NULL ");
return;
}
//当二叉树有根时
printf("%d ", root->val);
PrevOrder(root->left);
PrevOrder(root->right);
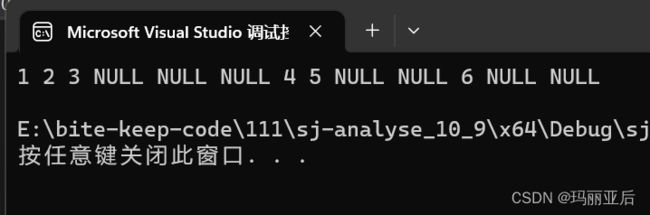
}通过递归我们可以很轻易地写出前序遍历,而接下来我们就来分析二叉树递归遍历的精妙之处~
递归时每次函数都会建立一个栈帧。
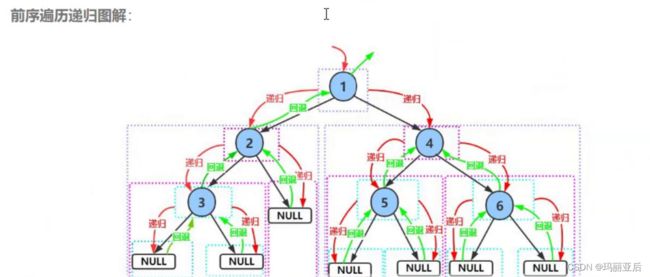
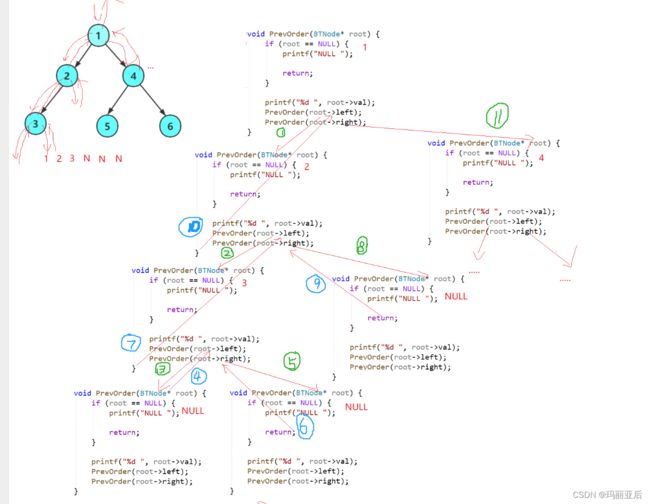
前序遍历递归展开图:
一开始根是1,打印出来后走1的左子树2,2作为根打印后继续走2的左子树3,3作为根打印后走3的左子树,但此时3的左子树为空所以递进结束开始回归,回到根为3的时候继续走3的右子树,然而3的右子树也是空所以不再递进选择回归。而当我们遍历完3的左右子树后就会回到2作为根的那一层栈帧,因为2的左子树3已经被我们遍历完了,所以我们开始遍历2的右子树,发现2的右子树也是空所以不再递进选择回归,把2的左右子树也遍历完后我们再回归至根为1的那一层,因为2作为1的左子树已经遍历完了,所以我们接着对1的右子树4选择递进........就这样以此类推,当所以子树都递进后最终都会向根回归,达到前序遍历的作用。
所以该递归最核心的部分就是先打印根结点,然后再去找根结点的左右子树,通过这个规律我们可以轻易的模仿出中序遍历与后序遍历。
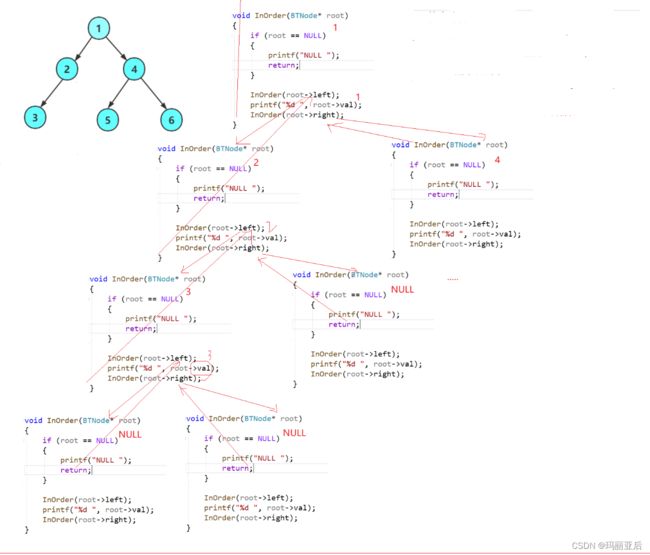
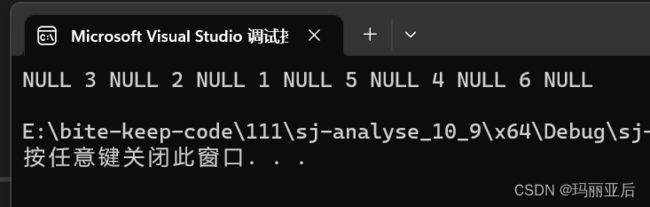
中序遍历递归图:
//中序遍历
void InOrder(BTNode* root)
{
//当二叉树无根时
if (root == NULL)
{
printf("NULL ");
return;
}
//当二叉树有根时
PrevOrder(root->left);
printf("%d ", root->val);
PrevOrder(root->right);
}后序遍历:
//后序遍历
void PostOrder(BTNode* root)
{
//当二叉树无根时
if (root == NULL)
{
printf("NULL ");
return;
}
//当二叉树有根时
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->val);
}2.3节点个数
节点个数其实很简单,只需要遍历一遍,遍历的时候计数就可以了,下面我们来用前序遍历计节点个数(其实中序和后序也可以遍历)
//节点个数 int TreeSize(BTNode* root) { int size = 0; //当二叉树无根时 if (root == NULL) { return 0; } else { size++; } //当二叉树有根时 PostOrder(root->left); PostOrder(root->right); return size; }注意,这种写法并不可取,因为我们在递归的时候都会建立栈帧,每一次递归都会建立一个size,这时候每一个size都是独立的,并不会叠加到同一个size上。
//节点个数 int TreeSize(BTNode* root) { static int size = 0; //当二叉树无根时 if (root == NULL) { return 0; } else { size++; } //当二叉树有根时 PostOrder(root->left); PostOrder(root->right); return size; }如果我们使用static就可以叠加size
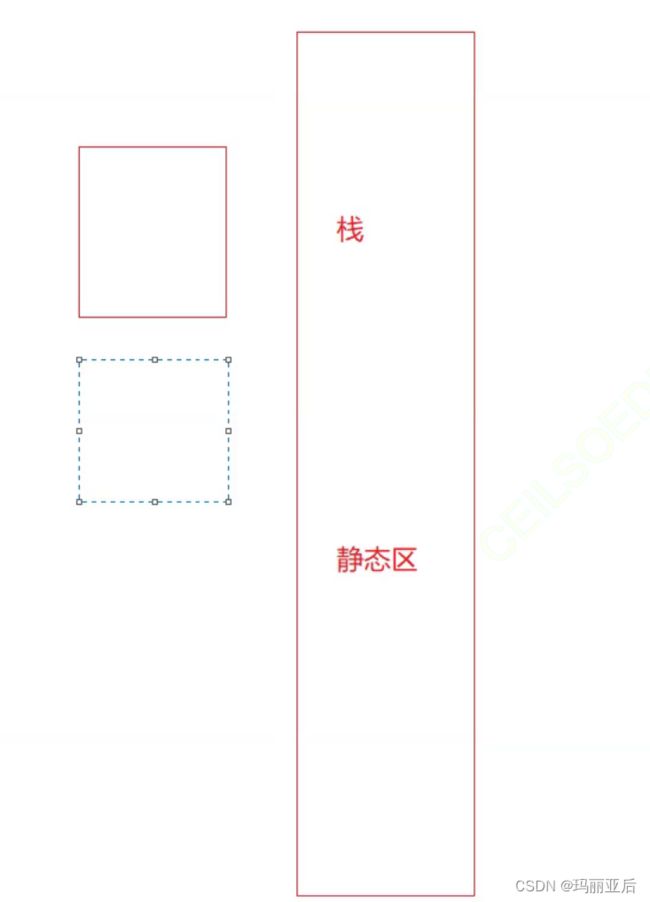
static int size是存放在静态区的,就不会受栈影响。但这种方法只能执行一次(计算一棵二叉树),如果我们要计算多棵二叉树的时候就不行了。(多次调用该函数节点数size会一直叠加,不会先初始化为0再计数)
//节点个数 int size = 0; int TreeSize(BTNode* root) { //当二叉树无根时 if (root == NULL) { return 0; } else { size++; } //当二叉树有根时 PostOrder(root->left); PostOrder(root->right); return size; }我们可以改用全局变量,然后每次调用完后再把size初始化为0即可。
当然最好的方法还是把它变成递归子问题:
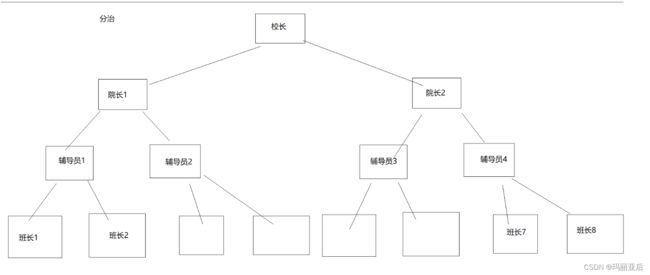
采用分治的思想,如果我们想要知道学校的全部人数,我们可以找校长,校长就去找2个院长...以此类推到最后的8个班长进行汇报,再一一传给上级直至校长。而在这层层分包的过程中——(由上而下遍历,由下而上累加计数)。
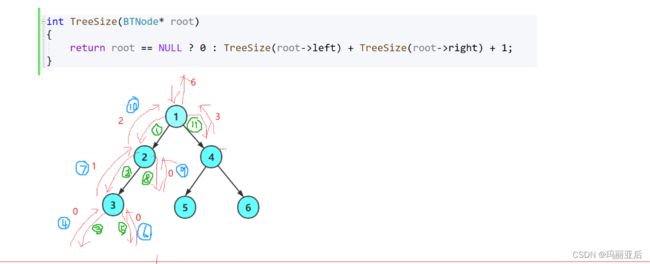
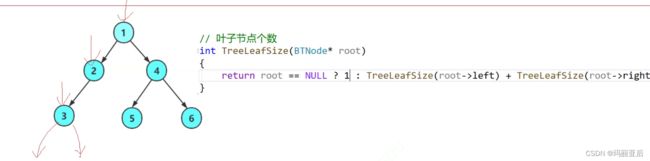
//节点个数 int TreeSize(BTNode* root) { return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1; }之所以要+1是因为我们在算出所在根左右子树节点个数的同时还需要加上根自己的个数。
严格来说这算是一种后序遍历,先求左右再求自己。
2.4叶子节点个数
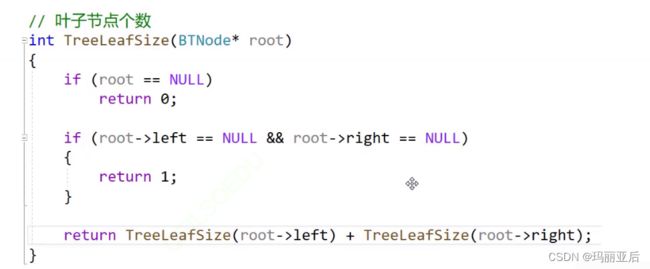
我们可以采用遍历左子树+右子树的形式(从左子树开始不断向下延申,到底后放返回去找右子树),递归返回左右子树相加的节点个数。方向是对的,但是注意我们写的是叶子节点的个数,不是上面代码所求空节点的个数,所以我们需要注意以下三点:
- 当该节点为空时返回0
- 当该节点是叶子时返回1
- 既不是空节点也不是叶子时返回左右子树相加
核心就在于辨别节点,当不是特殊节点时就要向下继续寻找它的左右子树的节点是否为特殊节点,一直持续到找到特殊节点(空或叶子节点)。
2.5第K层的节点个数
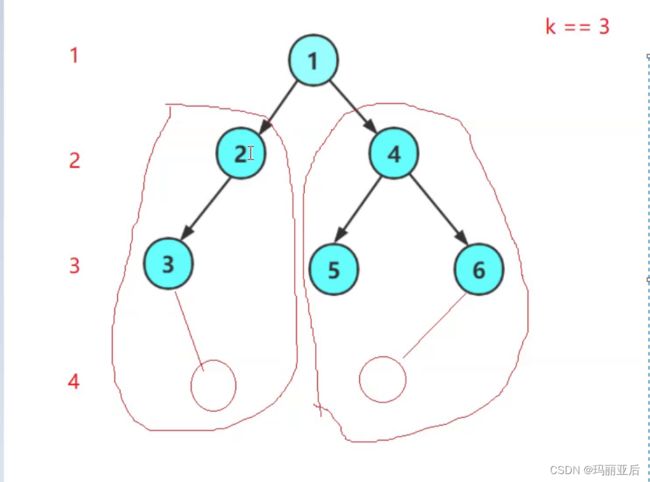
我们首先得知道层数是相对而言的,假设我们要求的是第三层,转换为子问题时对于左子树的2而言第三层在它看来是第二层。所以这一次不是用分治就能搞定的事情。
当前树的第k层 = 左子树的第k-1层 + 右子树的第k-1层
所求1的第三层转换为所求2的第二层再转换为所求3的第一层。当我们求到对应层数时(假设k=3,来到了第三层)如果第三层没有节点则返回0,反之返回1.
所以最后对于节点2而言,它所属的左右子树节点共返回了1个节点。
//第K层的节点数
int TreeKLevel(BTNode* root, int k)
{
assert(k > 0);
//该节点为空时
if (root == NULL)
{
return 0;
}
//到达目标层时
if (k == 1)
{
return 1;
}
return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}不同于与之前的判断左右子树为空后才返回1,由于是要求层节点所以我们要添加层数的限制,当到达所求层数时需要返回1,而所求层数的标准就是前面例子所假设的(k=3,对位于第三层的3而言它就是第一层)。到不了所求层数那就判定为空节点,直接返回0即可。
故基本思路就是一开始K为3,即第一层,那么我们肯定得优先判断第一层本身是否存在,不存在直接返回0,如果存在但又不满足我们所求层数则继续遍历它的左右子树,就这样持续下去直到我们能够成功到达目标楼层(K为1),不能到达肯定是因为前面的判断生效即该子树为空节点。所以最为核心的地方就是我们要弄清楚k楼层之间的相对关系。
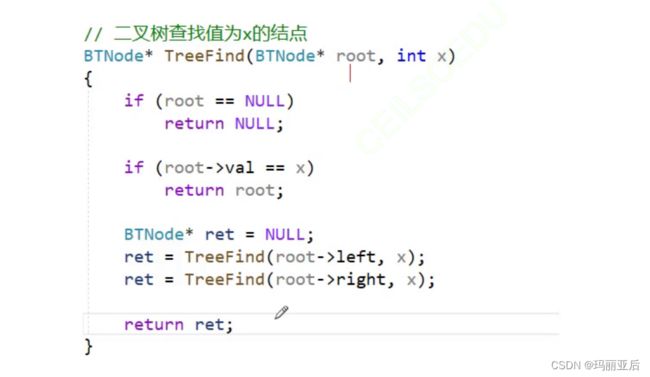
2.6 二叉树查找值为x的节点
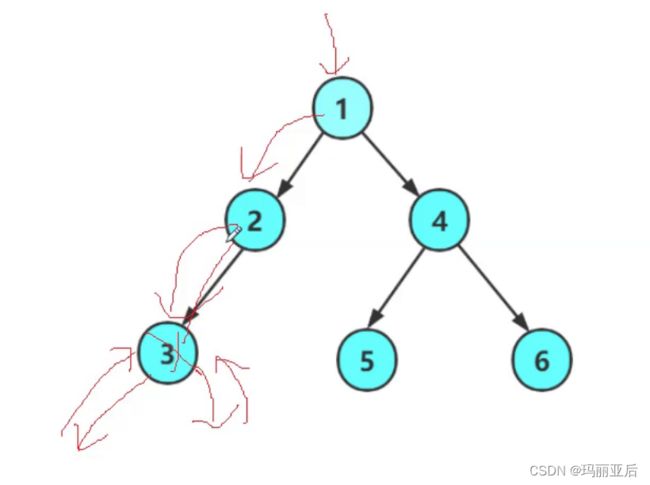
假设我们所寻值为3
从1开始遍历当找到所寻值3开始返回时并没有谁能够去接收这个返回节点。接收的意义有两层,一是接收找到的节点,二是判定找不到时继续去右子树寻找。这是一个层层往回返,层层接收的过程,不是说找到就能够直接返回的事情。
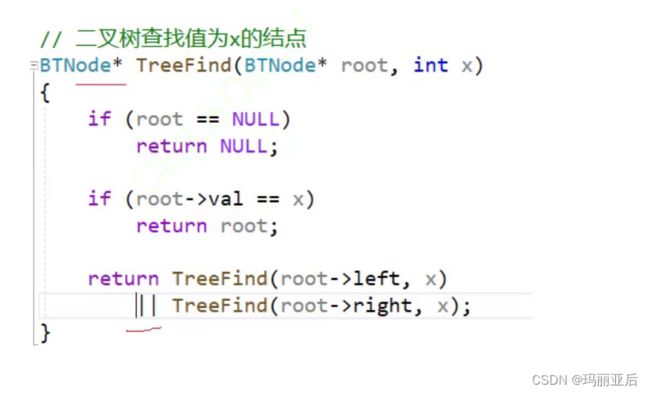
接下来看另外一个典型错误,这一次我们修改代码判断条件为||,如果左树找到就不用去右树找了。但是无论是或还是与它们最终的结果都只会是真与假即0与1,拿这个来作为节点的接收是很荒谬的。
这个错误是重复覆盖,虽然是多加了一个接收节点的指针,但是最终返回的永远都是右子树的节点,左子树一旦存储好节点遍历到右子树时还是会被其覆盖掉。
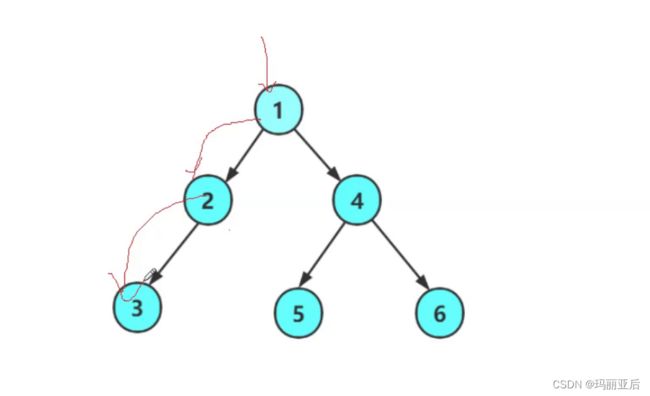
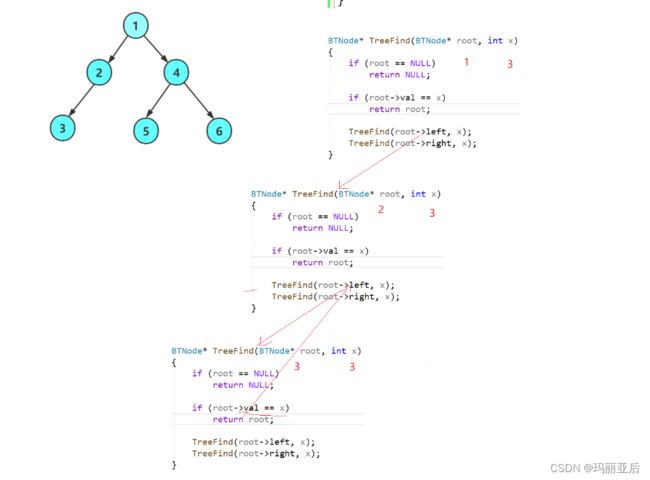
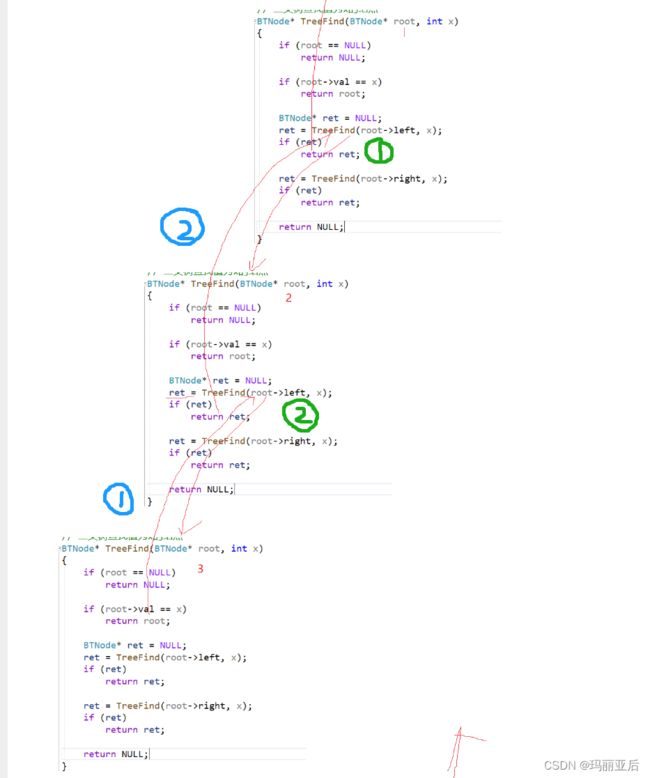
我们可以通过递归展开图来分析一下:
从1到2再到3本来就已经找到目标节点并且开始返回了,结果到2的时候又去遍历它的右子树去了,右子树为空返回空指针,把目标节点给覆盖了。所以我们设置接收节点还不够,还要分析什么时候才可以去遍历右子树。
//二叉树查找值为x的节点 BTNode* TreeFind(BTNode* root, int x) { //如果节点为空 if (root == NULL) { return NULL; } //如果节点不为空且数值刚好找到 if (root->val == x) { return root; } //设立接收节点 BTNode* ret = NULL; ret = TreeFind(root->left, x); if (ret) { return ret; } ret = TreeFind(root->right, x); if (ret) { return ret; } //如果再判断左右子树后接收节点仍为空,则最终返回空 return NULL; }上述代码才是正确写法,如果在左子树搜索到了就马上返回该节点到上一层,接着进行判断,如果接收节点指针ret不为空则代表找到,返回该节点。对于右子树也是同理,最后如果ret还是为空则代表没找到目的节点,返回NULL.
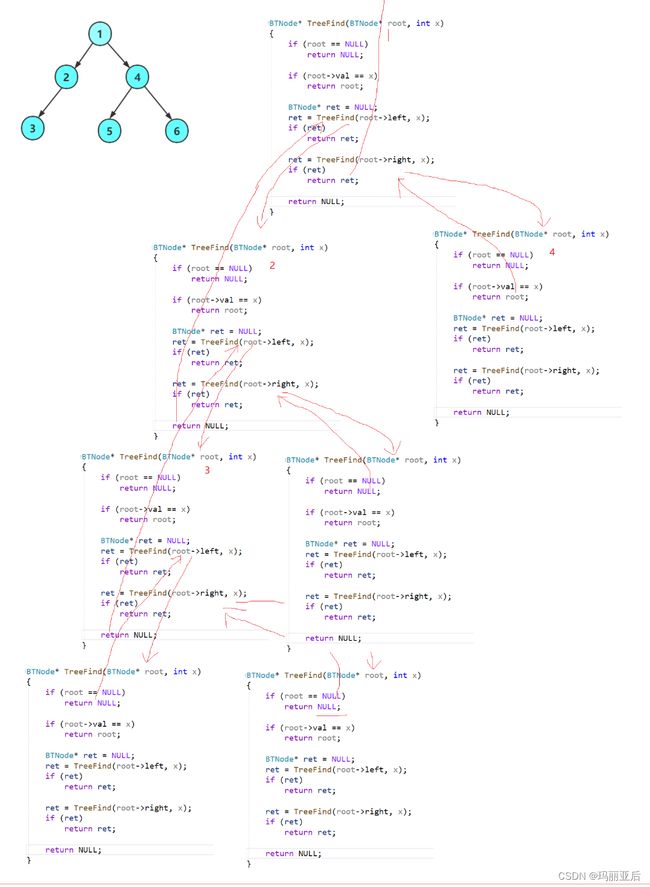
我们来分析一下递归展开图:
对左子树往下递归开始查找,但找到目的节点3时,将3这个节点返回到2节点处所设置的接收节点ret中,然后又判断ret不为空则return ret 继续返回到上一层即1节点处所设置的接收节点ret,判断不为空后才是返回到外面。
箭头的起点与终点都已经明确地表示的ret所存储的节点类别。
2.7 二叉树的销毁
这里的递归条件使用后序遍历可以很方便地把所以节点销毁,如果使用前序还得额外用指针去保存根节点。
//销毁节点 void TreeDestory(BTNode* root) { if (root == NULL) { return; } TreeDestory(root->left); TreeDestory(root->right); free(root); }核心就是通过遍历找到该子树最后的节点,然后依次从下往上销毁。左子树销毁完再去销毁右子树。
这里root==NULL可以直接替代root->left==NULL与root->right==NULL.
这里的root不需要去额外置空,因为这里面的形参不会影响到外面的实参。
 三.结语
三.结语
在csdn欠下的债我要在这个寒假还清!!!与君共勉~最后感谢大家的观看,友友们能够学习到新的知识是额滴荣幸,期待我们下次相见~