启发式算法解决TSP、0/1背包和电路板问题
1. Las Vegas
题目
设计一个 Las Vegas 随机算法,求解电路板布线问题。将该算法与分支限界算法结合,观察求解效率。
代码
python代码如下:
# -*- coding: utf-8 -*-
"""
@Date : 2024/1/4
@Time : 16:21
@Author : MainJay
@Desc : LasVegas算法解决电路问题
"""
import heapq
import random
maps = []
nums = 8
for i in range(nums):
m = []
for j in range(nums):
m.append(1 if random.random() < 0.3 else 0)
maps.append(m)
b_x = random.randint(0, nums - 1)
b_y = random.randint(0, nums - 1)
e_x = random.randint(0, nums - 1)
e_y = random.randint(0, nums - 1)
while maps[b_x][b_y] == 1:
b_x = random.randint(0, nums - 1)
b_y = random.randint(0, nums - 1)
while maps[e_x][e_y] == 1:
e_x = random.randint(0, nums - 1)
e_y = random.randint(0, nums - 1)
class Position(object):
targetPosition = None
def __init__(self, x: int, y: int, length: int = 0):
self.x = x
self.y = y
self.length = length
def __lt__(self, other):
return self.length + abs(Position.targetPosition.x - self.x) + abs(Position.targetPosition.y - self.y) - (
other.length + abs(Position.targetPosition.x - other.x) + abs(Position.targetPosition.y - other.y))
class LasVegas(object):
def __init__(self, initPosition: Position, targetPosition: Position):
self.initPosition = initPosition
Position.targetPosition = targetPosition
def run(self):
priority_queue = []
heapq.heappush(priority_queue, self.initPosition)
directions = [[-1, 0], [1, 0], [0, -1], [0, 1]]
flag = False # 判断是否找到了解
print(f"目标位置:{Position.targetPosition.x},{Position.targetPosition.y}")
while priority_queue:
item = heapq.heappop(priority_queue)
print(f"现在位置:{item.x}, {item.y}")
if item.x == Position.targetPosition.x and item.y == Position.targetPosition.y:
flag = True
# 找到解跳出
break
# 遍历
can_position = []
for direction in directions:
t_x = item.x + direction[0]
t_y = item.y + direction[1]
if 0 <= t_x < len(maps) and 0 <= t_y < len(maps[0]):
if maps[t_x][t_y] == 0: # 没有标记且没有墙
can_position.append(Position(t_x, t_y, item.length + 1))
if len(can_position) > 0:
# LasVegas算法随机挑选一个放入队列
m_position = can_position[random.randint(0, len(can_position) - 1)]
# 挑选的这个标记为已经走过
maps[m_position.x][m_position.y] = 2
heapq.heappush(priority_queue, m_position)
return flag
begin = Position(b_x, b_y)
end = Position(e_x, e_y)
l = LasVegas(begin, end)
l.run()
运行结果
[1, 0, 0, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0, 1, 1]
[1, 1, 0, 0, 0, 0, 0, 0]
[0, 1, 0, 0, 1, 0, 1, 0]
[1, 0, 0, 0, 0, 0, 0, 1]
[0, 1, 0, 0, 1, 1, 1, 0]
[0, 1, 0, 0, 1, 0, 0, 0]
目标位置:5, 6
现在位置:3, 4
现在位置:3, 5
现在位置:4, 5
现在位置:5, 5
现在位置:5, 6
2. 模拟退火算法
题目
上机实现TSP的模拟退火算法,随机生成一定规模的数据或用通用数据集比较其它人的结果,分析算法的性能,摸索实现中技术问题的解决。
代码
python代码如下:
# -*- coding: utf-8 -*-
"""
@Date : 2024/1/3
@Time : 16:15
@Author : MainJay
@Desc : 模拟退火算法解决TSP问题
"""
import random
from math import exp
import matplotlib.pyplot as plt
def create_new(ans: list):
"""
随机产生一个解
:param ans: 原解
:return: 返回一个解
"""
random_index1 = random.randint(0, len(ans) - 1)
random_index2 = random.randint(0, len(ans) - 1)
ans[random_index1], ans[random_index2] = ans[random_index2], ans[random_index1]
return ans
def create_distance(nums: int = 25):
"""
随机生成距离矩阵
:param nums: 城市数量
:return: 矩阵函数
"""
distance = []
for i in range(nums):
d = []
for j in range(nums):
if i > j:
d.append(distance[j][i])
elif i == j:
d.append(0)
else:
d.append(random.randint(0, 100) + random.random())
distance.append(d)
return distance
class SimulatedAnnealing(object):
def __init__(self, distance: list, initialTemperature: float = 100, endTemperature: float = 10, L: int = 5,
alpha: float = 0.05):
"""
:param distance: 距离矩阵
:param initialTemperature: 初始温度
:param endTemperature: 退火温度
:param L: 每个温度的迭代次数
:param alpha: 每次退火分数
"""
self.distance = distance
self.temperature = initialTemperature
self.endTemperature = endTemperature
self.L = L
self.result = [] # 记录每次退火过程中的最优解
self.t = [] # 记录每次退火过程中的温度,用于画图
self.alpha = alpha
def temperature_down(self):
"""
温度退火
:return:
"""
self.temperature = self.temperature * (1 - self.alpha)
def cal_ans(self, ans: list):
"""
计算解的值
:param ans: 解
:return: 解的权值
"""
val = 0.00
for i in range(0, len(ans) - 1):
val += self.distance[ans[i]][ans[i + 1]]
val += self.distance[ans[-1]][ans[0]]
return val
def annealing(self):
"""
模拟退火过程
:return:
"""
ans = list(range(len(self.distance))) # 随机初始化一个解
val = self.cal_ans(ans)
while self.temperature > self.endTemperature: # 直到温度降到指定结束温度时结束退火过程
for i in range(self.L): # 在每个温度迭代L次
new_ans = create_new(ans)
new_val = self.cal_ans(new_ans)
df = new_val - val
if df < 0:
ans, val = new_ans, new_val
elif random.uniform(0, 1) < 1 / (exp(df / self.temperature)):
ans, val = new_ans, new_val
self.result.append(val)
self.t.append(self.temperature)
self.temperature_down()
def plot(self):
# 在生成的坐标系下画折线图
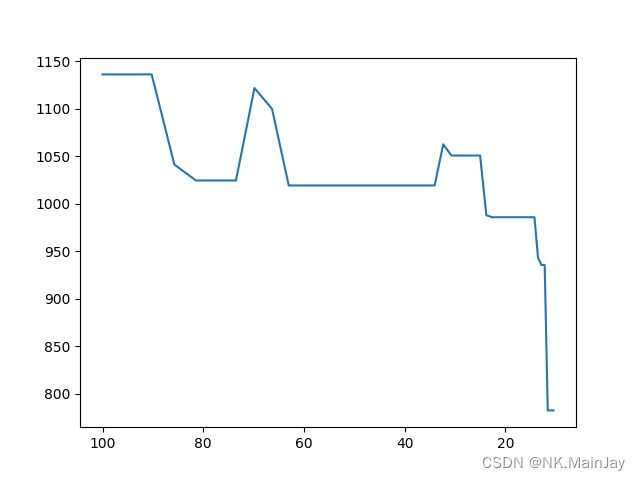
plt.plot(self.t, self.result)
plt.gca().invert_xaxis()
# 显示图形
plt.show()
distance = create_distance()
simulatedAnnealing = SimulatedAnnealing(distance)
simulatedAnnealing.annealing()
simulatedAnnealing.plot()
运行结果
3. 遗传算法
题目
上机实现 0/1 背包问题的遗传算法,分析算法的性能。
代码
python代码如下:
# -*- coding: utf-8 -*-
"""
@Date : 2024/1/4
@Time : 14:45
@Author : MainJay
@Desc : 遗传算法解决0/1背包问题
"""
import random
import heapq
import copy
import matplotlib.pyplot as plt
nums = 10
weights = []
values = []
W = 400
for i in range(nums):
weights.append(random.randint(0, 100))
values.append(random.randint(0, 100))
class GeneticAlgorithm(object):
def __init__(self, N: int = 6, Nums: int = 10, Mutation_probability: float = 0.1, iter_num: int = 10):
self.N = N
self.Nums = Nums
self.iter_num = iter_num
# 初始化种群
self.population = []
self.Mutation_probability = Mutation_probability
for i in range(N):
p = []
for j in range(len(weights)):
p.append(random.randint(0, 1))
self.population.append(p)
def selectNPopulation(self, population: list):
"""
挑选一个种群
:param population: 原始种群
:return: 新种群
"""
nums = 0
# 创建一个空的优先队列
priority_queue = []
for item in population:
heapq.heappush(priority_queue, Individual(item))
pops = []
total_v = 0.00
p = []
# 优胜虐汰,挑选前Nums满足条件的
while priority_queue and nums < self.Nums:
item = heapq.heappop(priority_queue)
if item.total_weight > W:
continue
pops.append(item.chromosome)
total_v += item.total_value
p.append(total_v)
nums += 1
p = [item / total_v for item in p]
# 根据概率分布随机挑选一个
new_pop = []
for i in range(self.N):
rand = random.random()
for j in range(len(p)):
if rand <= p[j]:
new_pop.append(pops[j])
break
return new_pop
def cross_population(self, population: list):
parents = copy.deepcopy(population)
for i in range(self.N):
mother = parents[random.randint(0, len(parents) - 1)]
father = parents[random.randint(0, len(parents) - 1)]
threshold = random.randint(0, len(weights) - 1)
sun1 = mother[:threshold] + father[threshold:]
sun2 = father[:threshold] + mother[threshold:]
population.append(sun1)
population.append(sun2)
return population
def population_variation(self, population: list):
"""
种群基因突变
:param population: 种群
:return: 一个种群
"""
if random.random() < self.Mutation_probability:
rand_pop = random.randint(0, len(population) - 1)
rand_index = random.randint(0, len(weights) - 1)
population[rand_pop][rand_index] = 1 - population[rand_pop][rand_index]
return population
def genetic(self):
x = []
y = []
for i in range(self.iter_num):
print(f"第{i + 1}代")
print(f"种群为{self.population}")
x.append(i + 1)
y.append(Individual(self.population[0]).total_value)
s_pop = self.selectNPopulation(self.population)
c_pop = self.cross_population(s_pop)
p_pop = self.population_variation(c_pop)
self.population = p_pop
self.plot(x, y)
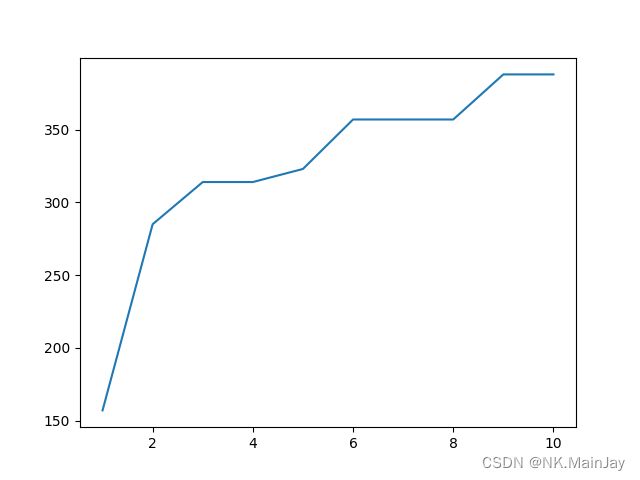
def plot(self, x, y):
# 在生成的坐标系下画折线图
plt.plot(x, y)
# 显示图形
plt.show()
class Individual(object):
def __init__(self, chromosome: list):
"""
:param chromosome: 染色体的列表
"""
self.chromosome = chromosome
self.total_weight = 0.00
self.total_value = 0.00
for i in range(len(chromosome)):
if chromosome[i] == 1:
self.total_weight += weights[i]
self.total_value += values[i]
def __lt__(self, other):
return self.total_value > other.total_value
g = GeneticAlgorithm()
g.genetic()
运行结果
第1代
种群为[[0, 0, 1, 1, 0, 0, 0, 0, 0, 0], [1, 0, 1, 0, 0, 1, 1, 0, 0, 0], [1, 1, 1, 0, 1, 0, 1, 0, 1, 0], [1, 0, 1, 0, 0, 0, 1, 0, 1, 1], [1, 1, 1, 1, 1, 0, 0, 1, 0, 0], [1, 1, 0, 1, 0, 1, 1, 1, 1, 1]]
第2代
种群为[[1, 0, 1, 0, 0, 0, 1, 0, 1, 1], [1, 1, 0, 1, 0, 1, 1, 1, 1, 1], [1, 1, 1, 0, 1, 0, 1, 0, 1, 0], [1, 0, 1, 0, 0, 0, 1, 0, 1, 1], [1, 1, 1, 1, 1, 0, 0, 1, 0, 0], [0, 0, 1, 1, 0, 0, 0, 0, 0, 0], [1, 1, 0, 1, 0, 1, 1, 0, 1, 1], [1, 0, 1, 0, 0, 0, 1, 1, 1, 1], [1, 1, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 0, 1, 0, 0, 1, 0, 0], [1, 1, 1, 1, 1, 0, 0, 1, 0, 0], [1, 1, 1, 0, 1, 0, 1, 0, 1, 0], [1, 1, 1, 0, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 1, 0, 0, 1, 0, 0], [1, 1, 0, 1, 0, 1, 1, 1, 1, 1], [1, 0, 1, 0, 0, 0, 1, 0, 1, 1], [1, 0, 1, 0, 0, 0, 1, 1, 1, 1], [1, 1, 0, 1, 0, 1, 1, 0, 1, 1]]
第3代
种群为[[1, 1, 1, 1, 1, 0, 0, 1, 0, 0], [1, 1, 0, 1, 0, 1, 1, 1, 1, 1], [1, 0, 1, 0, 0, 0, 1, 1, 1, 1], [1, 0, 1, 0, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 1, 0, 0, 1, 0, 0], [1, 1, 1, 1, 0, 0, 1, 0, 1, 1], [1, 1, 1, 1, 0, 0, 1, 0, 1, 1], [1, 1, 0, 1, 0, 1, 1, 1, 1, 1], [1, 0, 1, 1, 1, 0, 1, 1, 1, 1], [1, 0, 1, 0, 0, 0, 0, 1, 0, 0], [1, 1, 1, 1, 1, 0, 0, 1, 0, 0], [1, 0, 1, 1, 1, 0, 0, 1, 0, 0], [1, 0, 1, 0, 0, 0, 1, 0, 1, 1], [1, 1, 0, 1, 0, 1, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 1, 1, 0, 0, 0, 1, 0, 1, 1], [1, 0, 1, 0, 0, 0, 1, 1, 1, 1], [1, 0, 1, 0, 0, 0, 1, 0, 1, 1]]
第4代
种群为[[1, 1, 1, 1, 1, 0, 0, 1, 0, 0], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 0, 0, 0, 1, 1, 1, 1], [1, 0, 1, 0, 0, 0, 1, 1, 1, 1], [1, 1, 0, 1, 0, 1, 1, 1, 1, 1], [1, 1, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 1, 0, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 1, 0, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 1, 1, 0, 0, 0, 1, 1, 1, 1], [1, 0, 1, 0, 0, 0, 1, 1, 1, 1], [1, 0, 1, 0, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 1, 1, 0, 0, 0, 1, 1, 1, 1], [1, 1, 1, 1, 1, 0, 1, 1, 1, 1], [1, 0, 1, 0, 0, 0, 0, 1, 0, 0]]
第5代
种群为[[1, 1, 1, 0, 0, 0, 1, 1, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 1, 1, 0, 0, 0, 1, 1, 1, 1], [1, 1, 1, 0, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 1, 1, 0, 0, 1, 1, 1, 1, 1], [1, 0, 1, 0, 0, 0, 1, 1, 1, 1]]
第6代
种群为[[1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 1, 1, 0, 0, 0, 1, 1, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 1, 1, 0, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 1, 1, 0, 0, 0, 1, 1, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 1, 1, 0, 0, 0, 1, 0, 1, 1], [1, 0, 1, 0, 0, 1, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 1, 1, 0, 0, 0, 1, 1, 1, 1]]
第7代
种群为[[1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1]]
第8代
种群为[[1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1]]
第9代
种群为[[1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1]]
第10代
种群为[[1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 1, 1, 1, 1]]