（8-5-5）制作美股交易策略模型：使用有效前沿技术优化投资组合

在金融市场中，一种比较流行的做法是利用有效前沿技术来优化投资组合。有效前沿是一种图形表示技术，展示了在不同投资组合配置下风险和回报之间的权衡关系。通过分析这些股票的历史数据和预期收益以及它们之间的相关性，投资组合优化技术可以帮助投资者找到在给定风险水平下最大化回报或在期望回报水平下最小化风险的资产最优组合。这种方法使投资者能够做出明智的决策，实现投资多样化，并在管理风险的同时潜在地实现更高的回报，尤其是在这些重要的科技公司和由S&P 500代表的更广泛市场的背景下。

1. 分析公司收盘价之间的相关系数

通过了解谷歌、苹果、Facebook、亚马逊、微软和S&P 500的收盘价之间的相关系数，可以为我们提供关于个别股票价格与整体市场之间线性关系程度的见解。这些系数量化了这种关系的强度和方向，帮助投资者了解这些公司股票与更广泛市场之间的同步或分歧水平。

（1）计算GAFAM公司（谷歌、苹果、Facebook、亚马逊和微软）和S&P 500的收盘价之间的相关系数，并使用热力图可视化展示这些相关系数。

# 计算公司和S&P 500的收盘价之间的相关系数
corr = dataset[['GOOG', 'AAPL', 'META', 'AMZN', 'MSFT', 'GSPC']].corr()

# 使用热力图可视化相关系数
sns.heatmap(corr, xticklabels=corr.columns.values, yticklabels=corr.columns.values, annot=True, annot_kws={'size': 12})

# 调整图形大小和字体大小
heat_map = plt.gcf()
heat_map.set_size_inches(10, 6)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)

# 显示图形
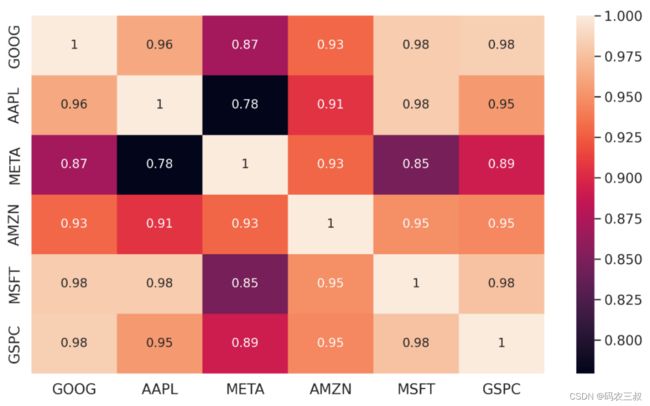
plt.show()

执行效果如图8-8所示，热力图中的颜色表示相关性的强弱，途中的注释显示了具体的相关系数数值。这有助于投资者了解不同股票之间的关联程度，为投资决策提供参考。

图8-8  每日股价的相关性热力图

这个每日股价的相关性热力图显示了S&P 500与Microsoft、Amazon与Microsoft之间以及Microsoft与Google、Google与Apple、Amazon与Microsoft之间的强正相关性。这些相关性表明这些公司的股价有向相似方向运动的倾向，突显了潜在的相互关联，为投资组合多样化策略提供了见解。

（2）公司收益率之间的相关系数

通过分析Google、Apple、Facebook、Amazon、Microsoft和S&P 500的收益率之间的相关系数，可以为我们提供一种衡量这些公司收益率与更广泛市场之间相互依赖或独立关系的方式，这能够帮助投资者评估将这些股票纳入其投资组合时的多样化潜力和相关风险。

下面代码通过计算GAFAM公司（谷歌、苹果、Facebook、亚马逊和微软）和S&P 500的收益率之间的相关系数，并使用热力图可视化展示这些相关系数。

# 计算公司和S&P 500的收益率之间的相关系数
corr = dataset[['R_GOOG', 'R_AAPL', 'R_META', 'R_AMZN', 'R_MSFT', 'R_GSPC']].corr()

# 使用热力图可视化相关系数，设置x轴和y轴标签以及注释显示
sns.heatmap(corr, xticklabels=corr.columns.values, yticklabels=corr.columns.values, annot=True, annot_kws={'size': 12})

# 调整图形大小和字体大小，显示热力图
heat_map = plt.gcf()
heat_map.set_size_inches(10, 6)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)

# 显示图形
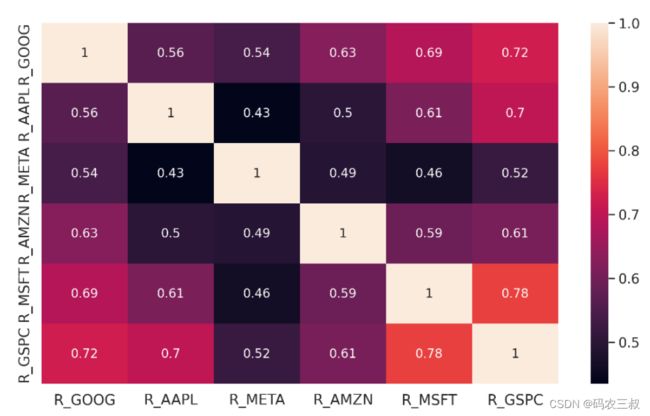
plt.show()

执行效果如图8-8所示。热力图中的颜色表示相关性的强弱，图中的注释显示具体的相关系数数值。这有助于投资者了解不同股票之间的收益率关联程度，为投资组合的多样化和风险评估提供参考。

图8-8  Returns价格的相关性热力图

Returns价格的相关性热力图显示了S&P 500的收益与Microsoft的收益之间强烈的正相关性。这表明它们有相似方向的运动趋势，暗示着整体市场表现的变化会影响到Microsoft的股票收益。下面是计算年化波动率和月度波动率的方法：

，

i={GOOG,AAPL,META,AMZN,MSFT,GSPC}

i={GOOG,AAPL,META,AMZN,MSFT,GSPC}

在上面的计算方法中，年化波动率是通过将每日波动率乘以252的平方根来计算的，其中252表示一年中的交易日数量。这是因为一年中通常有252个交易日。而月度波动率则是通过将每日波动率乘以21的平方根来计算的，其中21表示一个月中的交易日数量。这些计算适用于不同的资产，包括GOOG、AAPL、META、AMZN、MSFT以及整体市场的代表S&P 500。这些波动率计算有助于投资者更好地了解资产的风险水平。

注意：美股通常是每年有252个交易日，每个月有21个交易日。

（3）计算每支股票的年化波动率，并以百分比形式输出结果。其中，使用了252个交易日作为年度的计算基准。

returns  = dataset[['R_GOOG','R_AAPL','R_META','R_AMZN','R_MSFT', 'R_GSPC']]
n_days = 252
for col in returns.columns:
    print("The volatility of the stock of", col, "=",round(returns[col].std()*np.sqrt(n_days)*100,2), '% per year')

执行后会输出：

The volatility of the stock of R_GOOG = 26.82 % per year
The volatility of the stock of R_AAPL = 29.07 % per year
The volatility of the stock of R_META = 40.12 % per year
The volatility of the stock of R_AMZN = 32.28 % per year
The volatility of the stock of R_MSFT = 26.76 % per year
The volatility of the stock of R_GSPC = 17.39 % per year

我们可以看到，这期间Meta的年化波动率（40.12%）要高于其他股票。

（4）计算每支股票的月度波动率，并以百分比形式输出结果。其中，使用了21个交易日作为月度的计算基准。

returns  = dataset[['R_GOOG','R_AAPL','R_META','R_AMZN','R_MSFT', 'R_GSPC']]
n_days = 21
for col in returns.columns:
    print("The volatility of the stock of", col, "=",round(returns[col].std()*np.sqrt(n_days)*100,2), '% per month')

执行后会输出：

The volatility of the stock of R_GOOG = 7.74 % per month
The volatility of the stock of R_AAPL = 8.39 % per month
The volatility of the stock of R_META = 11.58 % per month
The volatility of the stock of R_AMZN = 9.32 % per month
The volatility of the stock of R_MSFT = 7.72 % per month
The volatility of the stock of R_GSPC = 5.02 % per month

我们可以看到，这期间Meta的月度波动率（11.58%）仍然高于其他股票。这说明Meta表现出更高的年化波动率（40.12%）比其他股票更高，表明其价格波动更为显著，潜在风险更大。甚至在每个月，Meta的波动性（11.58%）仍然高于其他股票，表明其价格波动较大。

2. 夏普比率

在金融市场中，夏普比率能够衡量类似Google、Apple、Facebook、Amazon、Microsoft和S&P 500这样的公司的风险调整回报。通过比较它们各自的夏普比率，我们可以评估每项投资在相对于风险水平产生回报方面的效率。较高的夏普比率表示更好的风险调整表现，意味着该投资在承担风险的同时提供了更高的回报。分析这些公司的夏普比率并将其与S&P 500进行比较，有助于投资者评估在平衡风险和回报方面，每个投资选项的相对吸引力。

计算夏普比率的公式如下：

1. Rp：投资组合的回报。
2. Rf ：无风险利率。
3. σp：投资组合超额回报的标准差。

下面代码定义了一个计算夏普比率的函数sharpe_ratio，该函数接受某支股票或投资组合的每日收益率序列以及无风险投资的年回报率（默认为0.025），计算并返回夏普比率。

n_days = 252

def sharpe_ratio(serie, rf=0.025):
    '''
    serie : 某支股票或投资组合的每日收益率序列
    rf: 无风险投资的年回报率（默认 rf=0.025）
    '''
    # 年化平均收益率
    rp = serie.mean() * n_days
    # 年度波动率
    volatility = serie.std() * np.sqrt(n_days)
    # 夏普比率
    sharpe = (rp - rf) / volatility
    return sharpe

然后计算每支股票的夏普比率，假设无风险投资的年回报率为2.5%。

# 假设无风险投资的年回报率为2.5%
# 计算每支股票的夏普比率
for col in returns.columns:
    print("The Sharpe ratio of,", col,"=", round(sharpe_ratio(returns[col]),2 ))

执行后会输出：

The Sharpe ratio of, R_GOOG = 0.67
The Sharpe ratio of, R_AAPL = 0.68
The Sharpe ratio of, R_META = 0.41
The Sharpe ratio of, R_AMZN = 0.69
The Sharpe ratio of, R_MSFT = 0.78
The Sharpe ratio of, R_GSPC = 0.53

夏普比率用于表示每单位风险的股票（或投资组合）的超额回报。在上面的输出结果中，S&P 500的夏普比率等于0.53。这表示在给定单位风险的情况下，与年回报率为2.5%的无风险投资相比，S&P 500的超额年回报率为53%。对于相同单位风险，微软的年度超额回报为78%，相比年回报率为2.5%的无风险投资。在这些条件下，最佳股票是微软，因为它具有最高的夏普比率。

夏普比率是评估股票或投资组合风险调整绩效的有价值的指标。在S&P 500的情况下，其夏普比率被计算为0.53。这意味着对于给定单位的风险，与年回报率为2.5%的无风险投资相比，S&P 500生成了53%的超额年回报。对于微软，其夏普比率表明相同水平的风险下，年度超额回报率为78%。这意味着与S&P 500相比，微软有潜力生成更高的回报。

基于这些发现，我们可以得出结论：微软在所分析的股票中表现出最高的夏普比率。这表明对于给定的风险水平，微软有潜力提供最佳的风险调整回报。因此，在夏普比率方面，微软是考虑的选项中最有利的股票选择。

3. Beta系数

Beta（贝塔）系数简称Beta，是衡量给定证券相对于市场（例如S&P 500）表现的指标。Beta传达以下信息：

1. β=0：表示与市场（即S&P 500）无关。
2. β=1：表示与市场表现相同。
3. β<1：表示与在经济衰退中损失较少，在经济繁荣时获利较少。
4. β>1：表示与在经济衰退中损失较多，在经济繁荣时获利较多。
5. β<0：表示与与市场呈负相关。也就是说，如果市场上涨，证券（与股票可互换使用）下跌，反之亦然。例如，黄金、白银、贵金属等。

接下来我们将尝试为Google、Apple、Facebook、Amazon、Microsoft和S&P 500找到Beta值。为了计算Beta值，通常考虑过去5年的数据，以每月为周期。计算公式如下：

β=

其中，i=GOOG,AAPL,META,AMZN,MSFT

（1）通过下面代码计算投资组合中每两个资产之间的协方差矩阵，并通过乘以12将月协方差年化。这个协方差矩阵在资产组合优化中用于计算风险。

执行后会输出：

R_GOOG R_AAPL R_META R_AMZN R_MSFT R_GSPC
R_GOOG 0.003426 0.002098 0.002770 0.002577 0.002345 0.001607
R_AAPL 0.002098 0.004025 0.002415 0.002237 0.002270 0.001689
R_META 0.002770 0.002415 0.007665 0.003033 0.002361 0.001728
R_AMZN 0.002577 0.002237 0.003033 0.004962 0.002432 0.001623
R_MSFT 0.002345 0.002270 0.002361 0.002432 0.003410 0.001719
R_GSPC 0.001607 0.001689 0.001728 0.001623 0.001719 0.001440

（2）下面代码分别计算了Google、Apple和Facebook相对于S&P 500的Beta系数。

beta_GOOG = cov.iloc[0,5] / cov.iloc[5,5]
print(f'Beta (10Y period) of Google is : {beta_GOOG}')


beta_AAPL = cov.iloc[1,5] / cov.iloc[5,5]
print(f'Beta (10Y period) of Apple is : {beta_AAPL}')


beta_META = cov.iloc[2,5] / cov.iloc[5,5]
print(f'Beta (10Y period) of Facebook is : {beta_META}')

执行后会输出：

Beta (10Y period) of Google is : 1.1160956781111853
Beta (10Y period) of Apple is : 1.1730606352218889
Beta (10Y period) of Facebook is : 1.200017516496074

Beta系数是衡量一个资产相对于市场波动的指标，上面的代码计算了过去10年的Beta系数，分别为Google约为1.12，Apple约为1.17，Facebook约为1.20。这些值表明这些公司的股价相对于整个市场有较强的正相关性，即它们在市场上的波动程度相对较高。

（3）下面代码分别计算了Amazon和Microsoft相对于S&P 500的Beta系数，以及S&P 500自身的Beta系数。Beta系数是衡量一个资产相对于市场波动的指标，这里将S&P 500的Beta系数通常被定义为1。

beta_AMZN = cov.iloc[3,5] / cov.iloc[5,5]
print(f'Beta (10Y period) of Amazon is : {beta_AMZN}')


Beta (10Y period) of Amazon is : 1.127099926299393
beta_MSFT = cov.iloc[4,5] / cov.iloc[5,5]
print(f'Beta (10Y period) of Microsoft is : {beta_MSFT}')


beta_GSPC = cov.iloc[5,5] / cov.iloc[5,5]
print(f'Beta (10Y period) of S&P 500 is : {beta_GSPC}')

执行后会输出：

Beta (10Y period) of Microsoft is : 1.1941011901897405
Beta (10Y period) of S&P 500 is : 1.0

上面的代码分别计算了过去10年的Beta系数，Amazon的Beta系数约为1.13，Microsoft的Beta系数约为1.19，而S&P 500的Beta系数为1.0。这些值表明Amazon和Microsoft的股价相对于整个市场有较强的正相关性，而S&P 500的Beta系数符合市场平均水平。

未完待续