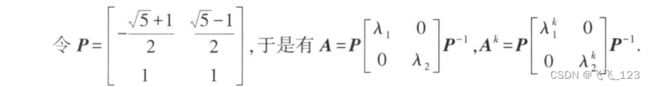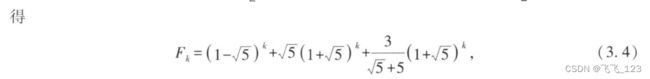Python数学建模之线性代数模型

• 本文只对已有数学模型进行Python代码的实现和解释，不分析模型的建立过程，模型的建立可查阅司守奎老师的《Python数学建模算法与应用》一书。

1.特征值与特征向量

1.差分方程

        解决此类问题需要使用sympy库函数，对于sympy库的详细介绍见这篇文章：

        http://t.csdnimg.cn/ImXiY

例：求斐波那契数列的通项公式。

解法一：运用特征值和特征向量求通项

sp.var('k', positive=True, integer=True)    # 定义一个正整数变量k
a = sp.Matrix([[0, 1], [1, 1]])     # 创建系数矩阵a，即A

 

val = a.eigenvals()                 # 求A的特征值
vec = a.eigenvects()                # 求A的特征向量

P, D = a.diagonalize()              # 把A相似对角化，并将特征值矩阵和相似变换矩阵分别赋值给变量D和P
ak = P @ (D**k) @ (P.inv())         # 求ak，即A^{k}。P.inv()表示矩阵P的逆矩阵

F = ak @ sp.Matrix([1, 1])          # 求F，即a_{k}

s = sp.simplify(F[0])               # 对乘积F中的第一个元素，即F_{k}进行化简
print(s)                            # 输出通项公式，即F_{k}

完整代码： 

import sympy as sp
sp.var('k', positive=True, integer=True)    # 定义一个正整数变量k
a = sp.Matrix([[0, 1], [1, 1]])     # 创建系数矩阵a，即A
val = a.eigenvals()                 # 求A的特征值
vec = a.eigenvects()                # 求A的特征向量
P, D = a.diagonalize()              # 把A相似对角化，并将特征值矩阵和相似变换矩阵分别赋值给变量D和P
ak = P @ (D**k) @ (P.inv())         # 求ak，即A^{k}。P.inv()表示矩阵P的逆矩阵
F = ak @ sp.Matrix([1, 1])          # 求F，即a_{k}
s = sp.simplify(F[0])               # 对乘积F中的第一个元素，即F_{k}进行化简
print(s)                            # 输出通项公式，即F_{k}
"""
将k逐个替换为0到19的整数，并计算s的数值，即输出斐波那契数列的前二十项。
.subs(k, i)表示将符号表达式s中的符号变量k替换为变量i，得到一个新的符号表达式。
.n()将这个新的符号表达式转换为数值，即进行数值计算。
"""
sm = []
for i in range(20):
    sm.append(int(s.subs(k, i).n()))
print(sm)

解法二：差分方程的特征根解法

sp.var('t, c1, c2')             # 定义了三个符号变量t、c1和c2
t0 = sp.solve(t**2-t-1)         # 求解特征方程t^{2}-t-1

# 定义了两个方程eq1和eq2，分别表示c1+c2-1=0和c1*t0[0]+c2*t0[1]-1=0
eq1 = c1+c2-1
eq2 = c1*t0[0]+c2*t0[1]-1

# 使用sp.solve()函数来解方程组，返回的是一个字典，包含方程组的解
s = sp.solve([eq1, eq2])
print('c1=', s[c1])
print('c2=', s[c2])

 完整代码：

import sympy as sp
sp.var('t, c1, c2')             # 定义了三个符号变量t、c1和c2
t0 = sp.solve(t**2-t-1)         # 求解特征方程t^{2}-t-1
# 定义了两个方程eq1和eq2，分别表示c1+c2-1=0和c1*t0[0]+c2*t0[1]-1=0
eq1 = c1+c2-1
eq2 = c1*t0[0]+c2*t0[1]-1
# 使用sp.solve()函数来解方程组，返回的是一个字典，包含方程组的解
s = sp.solve([eq1, eq2])
print('c1=', s[c1])
print('c2=', s[c2])

        这种方法适用于不知道系数矩阵，只知道它的特征方程，否则可以直接用eigenvals()函数求解特征根。

解法三：直接利用Python软件求解

较为简单，不做解释。

import sympy as sp
sp.var('k')                                     # 定义了一个符号变量k
y = sp.Function('y')                            # 定义了一个函数符号y，表示递归序列的通项公式
f = y(k+2)-y(k+1)-y(k)                          # 定义了递归序列的递推关系式
# 求解递归序列。sp.rsolve()函数接受三个参数：递推关系式、待求解的通项公式和初始条件，返回的结果为通项公式
s = sp.rsolve(f, y(k), {y(0):1, y(1):1})
print(s)

2.Leslie种群模型

X0 = np.array([500, 1000, 500])
L = np.array([[0, 4, 3], [0.5, 0, 0], [0, 0.25, 0]])

X1 = L @ X0
X2 = L @ X1
X3 = L @ X2

'''
sp.var('lamda')                  # 定义符号变量
p = Ls.charpoly(lamda)           # 计算矩阵Ls的特征多项式，并将结果赋值给变量p
w1 = sp.roots(p)                 # 计算特征值
'''
w2 = Ls.eigenvals()              # 直接计算特征值
v = Ls.eigenvects()              # 直接计算特征向量
P, D = Ls.diagonalize()          # 相似对角化，将结果分别赋值给对角矩阵D和相似变换矩阵P

Pinv = P.inv()                   # 求逆阵
Pinv = sp.simplify(Pinv)         # 简化矩阵Pinv
cc = Pinv @ X0
print('c=', cc[0])

 完整代码：

import numpy as np
import sympy as sp
X0 = np.array([500, 1000, 500])
L = np.array([[0, 4, 3], [0.5, 0, 0], [0, 0.25, 0]])
X1 = L @ X0
X2 = L @ X1
X3 = L @ X2
# Rational()函数将有理数表示为分数的形式，以保留精确的数值
Ls = sp.Matrix([[0, 4, 3],
    [sp.Rational(1, 2), 0, 0],
    [0, sp.Rational(1, 4), 0]])
'''
sp.var('lamda')                  # 定义符号变量
p = Ls.charpoly(lamda)           # 计算矩阵Ls的特征多项式，并将结果赋值给变量p
w1 = sp.roots(p)                 # 计算特征值
'''
w2 = Ls.eigenvals()              # 直接计算特征值
v = Ls.eigenvects()              # 直接计算特征向量
P, D = Ls.diagonalize()          # 相似对角化，将结果分别赋值给对角矩阵D和相似变换矩阵P
Pinv = P.inv()                   # 求逆阵
Pinv = sp.simplify(Pinv)         # 简化矩阵Pinv
cc = Pinv @ X0
print('c=', cc[0])

3.PageRank算法

1.基础的PageRank算法

# 计算矩阵W
L = [(1, 2), (2, 3), (2, 4), (3, 4), (3, 5),
    (3, 6), (4, 1), (5, 6), (6, 1)]
w = np.zeros((6, 6))                        # 邻接矩阵初始化
for i in range(len(L)):
    w[L[i][0]-1, L[i][1]-1] = 1
# 计算矩阵P
r = np.sum(w, axis=1, keepdims=True)
P = w/r                                     # 这里利用矩阵广播

"""
用eigs函数来计算矩阵P的特征值和对应的特征向量
P.T表示矩阵P的转置
参数1表示要计算的特征值和特征向量的数量,默认特征值按从大到小排列
eigs函数的返回值是一个元组(val, vec)，val是一个包含特征值的一维数组，vec是一个包含特征向量的二维数组
"""
val, vec = eigs(P.T, 1)
V = vec.real                                # 将特征向量vec的实部提取出来，赋值给变量V
V = V.flatten()                             # 将V展开成一维数组
V = V/V.sum()
print('V=', np.round(V, 4))

完整代码：

import numpy as np
from scipy.sparse.linalg import eigs
import pylab as plt
# 计算矩阵W
L = [(1, 2), (2, 3), (2, 4), (3, 4), (3, 5),
    (3, 6), (4, 1), (5, 6), (6, 1)]
w = np.zeros((6, 6))                        # 邻接矩阵初始化
for i in range(len(L)):
    w[L[i][0]-1, L[i][1]-1] = 1
# 计算矩阵P
r = np.sum(w, axis=1, keepdims=True)
P = w/r                                     # 这里利用矩阵广播
"""
用eigs函数来计算矩阵P的特征值和对应的特征向量
P.T表示矩阵P的转置
参数1表示要计算的特征值和特征向量的数量,默认特征值按从大到小排列
eigs函数的返回值是一个元组(val, vec)，val是一个包含特征值的一维数组，vec是一个包含特征向量的二维数组
"""
val, vec = eigs(P.T, 1)
V = vec.real                                # 将特征向量vec的实部提取出来，赋值给变量V
V = V.flatten()                             # 将V展开成一维数组
V = V/V.sum()
print('V=', np.round(V, 4))
# 用柱状图显示
plt.bar(range(1, len(w)+1), V, width=0.6, color='b')
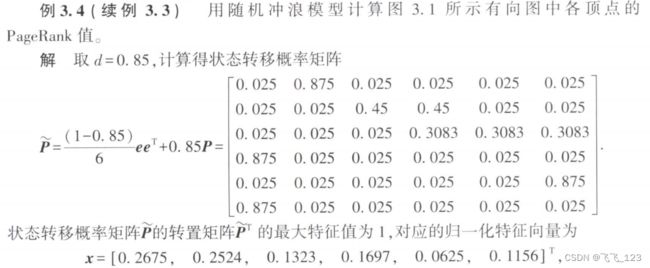
plt.show()

 2.随机冲浪模型的PageRank值

 代码：

import numpy as np
from scipy.sparse.linalg import eigs
import pylab as plt
L = [(1, 2), (2, 3), (2, 4), (3, 4), (3, 5),
    (3, 6), (4, 1), (5, 6), (6, 1)]
w = np.zeros((6, 6))
for i in range(len(L)):
    w[L[i][0]-1, L[i][1]-1] = 1
r = np.sum(w, axis=1, keepdims=True)
P = (1-0.85)/w.shape[0]+0.85*w/r            # 这里利用矩阵广播
val, vec = eigs(P.T, 1)
V = vec.real
V = V.flatten()                             # 展开成 (n, ) 形式的数组
V = V/V.sum()
print('V=', np.round(V, 4))
plt.bar(range(1, len(w)+1), V, width=0.6, color='b')
plt.show()

不做详细解释，使用时根据情况替换参数及可。 

2.矩阵的奇异值分解及应用

1.矩阵的奇异值分解

 求奇异值分解的代码如下，使用是将a替换为待求矩阵即可。

import numpy as np 
from numpy.linalg import svd
a = np.array([[1, 0, 1], [0, 1, 1], [0, 0, 0]])
u, s, vt = svd(a)       # a = u @ np.diag(s) @ vt
print(u); print(s); print(vt)

2.奇异值分解的应用

1.推荐系统的评分

txt文件的内容：

5	2	1	4	0	0	2	4	0	0	0
0	0	0	0	0	0	0	0	0	3	0
1	0	5	2	0	0	3	0	3	0	1
0	5	0	0	4	0	1	0	0	0	0
0	0	0	0	0	4	0	0	0	4	0
0	0	1	0	0	0	1	0	0	5	0
5	0	2	4	2	1	0	3	0	1	0
0	4	0	0	5	4	0	0	0	0	5
0	0	0	0	0	0	4	0	4	5	0
0	0	0	4	0	0	1	5	0	0	0
0	0	0	0	4	5	0	0	0	0	3
4	2	1	4	0	0	2	4	0	0	0
0	1	4	1	2	1	5	0	5	0	0
0	0	0	0	0	4	0	0	0	4	0
2	5	0	0	4	0	0	0	0	0	0
5	0	0	0	0	0	0	4	2	0	0
0	2	4	0	4	3	4	0	0	0	0
0	3	5	1	0	0	4	1	0	0	0

 解法一：非压缩数据的模型 

1）计算相似系数

2）评分估计

3）菜品推荐结果

import numpy as np
import pandas as pd
# np.loadtxt()函数会从文本文件中加载数据，并将其存储为一个NumPy数组
a = np.loadtxt('data3_6_1.txt')
# corrcoef(a.T)根据数组a计算相关系数，得到相关系数矩阵
# 再对结果进行归一化处理
b = 0.5*np.corrcoef(a.T)+0.5
# 使用Pandas将数组b转换为DataFrame，并将其保存为名为data3_6_2.xlsx的Excel文件，不包含索引
c = pd.DataFrame(b)
c.to_excel('data3_6_2.xlsx', index=False)
print('请输入人员编号1-18')
user = int(input())
# 获取数组a的列数，即变量的个数，并将其保存在变量n中
n = a.shape[1]
# np.where返回值的格式为(array([ 0,  1,  2,  3,  4,  5,  6,  7,  8, 10], dtype=int64),)，取0号元素，即为所有未评分编号
no = np.where(a[user-1,:]==0)[0]
# set函数用于创建一个无序且不重复的集合对象，此处用集合操作得到已评分编号的集合
yb = set(range(n))-set(no)
# 转化为列表
yb = list(yb)
# 从数组a中获取第user-1行中已评分编号对应的分数，并将其保存在数组ys中
ys = a[user-1, yb]
"""
创建一个长度为未评分编号的个数的零数组，并将其保存在数组sc中
对于每个未评分编号，计算其与已评分编号的相似度，并将计算结果保存在数组sc中
根据已评分的分数值估计出未评分的项目可能的分数
"""
sc = np.zeros(len(no))                      
for i in range(len(no)):
    sim = b[no[i], yb]
    sc[i] = ys @ sim/sum(sim)
print('未评分项的编号为：', no+1)
print('未评分项的分数为：', np.round(sc, 4))

解法二：基于奇异值分解压缩数据的模型

1）稀疏矩阵的降维处理

2）衡量菜品之间的相似性

3）评分估计

4）菜品推荐结果

import numpy as np
import pandas as pd
a = np.loadtxt('data3_6_1.txt')
# 使用numpy的linalg.svd()函数对矩阵a进行奇异值分解，分别得到左奇异向量矩阵u、奇异值向量sigma和右奇异向量矩阵vt
u, sigma, vt = np.linalg.svd(a)
print(sigma)
# cumsum()函数的返回值是一个数组，第i个元素是sigma的0到i号元素的平方和
cs = np.cumsum(sigma**2)
# 将奇异值累积平方和除以总和，得到一个包含每个奇异值贡献率的数组
rate = cs/cs[-1]
"""
找到第一个满足累积贡献率大于等于0.9的索引，并将其加1，得到奇异值的个数ind
这个值表示保留多少个奇异值，使得它们的累积贡献率达到了90%
这样做的目的是为了尽可能保留数据中的主要信息，同时实现数据降维的目标
"""
ind = np.where(rate>=0.9)[0][0]+1
# 构建一个对角矩阵，其对角线元素为前ind个奇异值，然后通过矩阵乘法得到降维后的数据b
b = np.diag(sigma[:ind]) @ u.T[:ind, :] @ a
# 使用np.linalg.norm()函数计算矩阵b的每列的范数，并保持维度为1
c = np.linalg.norm(b, axis=0, keepdims=True)    
# 计算相似度矩阵d，并归一化
d = 0.5*b.T @ b/(c.T @ c)+0.5   
# 其余步骤与解法一相同
dd = pd.DataFrame(d)
dd.to_excel('data3_6_3.xlsx', index=False)
print('请输入人员编号1-18')
user = int(input())
n = a.shape[1]                                  
no = np.where(a[user-1,:]==0)[0]                
yb = set(range(n))-set(no)                      
yb = list(yb)
ys = a[user-1, yb]                              
sc = np.zeros(len(no))                        
for i in range(len(no)):
    sim = d[no[i], yb]
    sc[i] = ys @ sim/sum(sim)
print('未评分项的编号为：', no+1)
print('未评分项的分数为：', np.round(sc, 4))

2.利用SVD进行图像压缩

在数学建模中几乎用不到，了解即可。

import numpy as np
from numpy import linalg as LA 
from PIL import Image
import pylab as plt                 # 加载 Matplotlib 的 pylab 接口
plt.rc('font', size=13) 
plt.rc('font',family='SimHei')
a = Image.open('Lena.bmp')          # 返回一个 PIL 图像对象
if a.mode!='L':
    a = a.convert('L')              # 转换为灰度图像
b = np.array(a).astype(float)       # 把图像对象转换为数组
[p, d, q] =  LA.svd(b)
m, n = b.shape
R = LA.matrix_rank(b)               # 图像矩阵的秩
plt.figure(0)
plt.plot(np.arange(1, len(d)+1), d, 'k.')
plt.ylabel('奇异值'); plt.xlabel('序号')
plt.title('图像矩阵的奇异值')
CR = []
for K in range(1, int(R/4), 10):
    plt.figure(K)
    plt.subplot(121)
    plt.title('原图')
    plt.imshow(b, cmap='gray')
    I = p[:, :K+1] @ (np.diag(d[:K+1])) @ (q[:K+1, :])
    plt.subplot(122)
    plt.title('图像矩阵的秩='+str(K))
    plt.imshow(I, cmap='gray')
    src = m*n
    compress = K*(m+n+1)
    ratio = (1-compress/src)*100    # 计算压缩比率
    CR.append(ratio)
    print('Rank=%d:K=%d个:ratio=%5.2f'%(R, K ,ratio))
plt.figure();
plt.plot(range(1, int(R/4), 10), CR, 'bo-')
plt.title('奇异值个数与压缩比率的关系')
plt.xlabel('奇异值个数')
plt.ylabel('压缩比率')
plt.show()