递归算法的时间复杂度和空间复杂度

时间复杂度和空间复杂度的概念

时间复杂度：语句执行的次数，一定与问题规模相关的
空间复杂度：额外开辟的(实现该算法额外的辅助空间)，与问题规模n相关的内存空间

递归流程分析

案例1

int Fun1(int n){
	if(n<=1)
		return n;
	else 
		return Fun1(n-1)+1;
}

以n为3为例说明
当n为3时，调用Fun(3),就会在栈开辟一块大小为一个C的空间

由于n不小于等于1，所以再次调用Fun(2),在栈开辟空间，判断2不小于等于1，所以再次调用Fun(1),在栈开辟空间，由于前面的函数调用没有结束，因此该栈空间并不会释放。

此时n等于1，满足Fun(1)返回条件,，所以释放Fun(1)内存，调用结束,将结果1返回给调用处，即Fun(2),

当Fun(2)接收到Fun(1)返回的1，Fun(2)就可以返回2给调用处Fun(3),并且释放该内存。

当Fun(3)接收到Fun(2)返回的2，Fun(3)就可以直接返回3,并且释放该Fun(3)内存。

至此，该递归函数Fun(3)正式结束。
注意：只有堆内存才需要程序员自己申请和释放，该栈内存是系统内部自己开辟释放的。

逐层调用，依次返回

表面上看这个的时间复杂度像是 O(1),但实际上当然不是。为什么呢?因为Fun1(n)会调用Fun1(n-1),再调
用 Fun1(n-2),Fun1(n-3),…,Fun1(1)。
函数调用也是需要时间的,假设函数调用的时间为常数 c,那么这么多次函数调用的总时间为c*n;c 为系数
可以忽略,那么时间复杂度为 O(f(n)) = O(n)。
案例2

int Fun2(int n){
	if(n<=1)
		return n;
	else 
		return Fun2(n-2)+2;
}

函数调用的关系为 Fun2(n)调用 Fun2(n-2),Fun2(n-4),…,Fun2(1)或 者 Fun2(0),总调用次数为 n/2次,所
以时间复杂度为 O(f(n))=O(n)
案例3

int Fun3(int n){
	if(n<=1)
		return n;
	else 
		return Fun3(n/2)+1;
}

由于该函数一直除2，问题规模是n，即问，n除2的多少次方为1，所以时间复杂度为O(logN)

时间复杂度效率排序

常见的时间复杂度效率为：
O(1)

斐波那契数列递归实现详解

斐波那契数列时间复杂度分析

题目
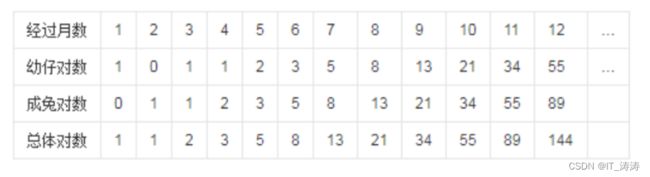
斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契
（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：这个数列从第3项开始，每一项都等于前两项之和
递归实现代码

int fib(int n){
	if(n<=n)
		return 0;
	if(n<=3)
		return 1;
	return fib(n-1)+fib(n-2);

以fib(5)为例：

求f(n)的过程可以用一颗二叉树表示,树中的每个节点就代表一次基本计算。易知，树的高度为n，一棵高度为n的满二叉树的节点个数为2n-1，当然，上图中的树肯定不是满二叉树，但也可以看出来，该树的节点个数大于满二叉树节点数的一半,即

(2n-1)/2。设计算次数为f(n),可知
(2^n-1)/2 <f(n) <2^n-1.

所以时间复杂度是O(2^n)

斐波那契数列空间复杂度分析

这里提供一个公式：
递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度
为什么要求递归的深度呢？
因为每次递归所需的空间都被压到调用栈里（这是内存管理里面的数据结构，和算法里的栈原理是一样的），一次递归结束，这个栈就是就是把本次递归的数据弹出去。所以这个栈最大的长度就是递归的深度。此时可以分析这段递归的空间复杂度，从代码中可以看出每次递归所需要的空间大小都是一样的，所以每次递归中需要的空间是一个常量，并不会随着n的变化而变化，每次递归的空间复杂度就是O(1)。
fib(4)中函数调用

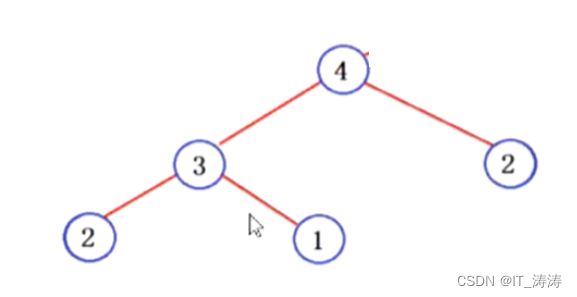
fib(4)中栈的开辟流程图

由该图很好的验证了下面的公式：
递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度
所以空间复杂度是O(n)

斐波那契数列非递归实现

1使用空间换时间

int fib(int n){
	int*data=(int*)malloc(sizeof(int)*n);
	data[0]=0;
	data[1]=1;
	for(int i=3;i<n;i++){
		data[i]=data[i-1]+data[i-2];
	}
	int c=data[n-1];
	free(data);
	data=NULL;
	return c;
}

时间复杂度：O(n);
空间复杂度：O(n);

2相对来说，最优的解法

int fib(int n){
	int a=0,b=1,c-1;
	if(n==1)return a;
	if(n==2)return b;
	for(int i=3;i<=n;i++){
		c=a+b;
		b=a;
		a=c;
	}
	return c;
}
	

时间复杂度：O(n);
空间复杂度：O(1);

斐波那契数列练习题

1）有一段楼梯有10级台阶，规定每一步只能跨一级或两级，要登上第 10 级台阶有几种不同的走法?
2）一枚均匀的硬币掷10次，问不连续出现正面的可能情形有多少种？
S1 = 2 ， S2 = 3 ，S3 = 5 ，S4 = 8…
3）兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔子都不死，
那么一年以后可以繁殖多少对兔子？