数据结构与算法:哈夫曼树与哈夫曼编码
数据结构与算法:哈夫曼树与哈夫曼编码(编码部分下期讲)
1.1哈夫曼树的由来
哈夫曼树是由麻省理工学院的哈夫曼博士于1951年发明的。
1.2哈夫曼树的作用以及用途理解,方便后续对于这种算法的理解。
虚构的:比如说,从前古代,人们带兵打仗两军交战,各个将领手下都有那些善于刺探敌情的卧底,那些卧底在敌营潜伏的时候,肯定要向外界传递信息,传递信息又必须得保证信息的完整性和安全性,于是他们就想到了压缩信息,精简传递的办法,这种方法不仅可以压缩信息,还可以根据对应编码,等到达我方营地的时候进行解码,且不会有失真的情况存在。
在这里,就要引入我们将要进行讲解的哈夫曼树了,哈夫曼树就是一种压缩的简单算法。
2.1哈夫曼树的概念
2.1.1定义
在n个带权叶子结点构成的所有二叉树中,带权路径长度WPL最小的二叉树称为哈夫曼树(英语就不摆了,大家都不看)或者最优二叉树。
2.1.1.1名词解释
权值,在许多二叉树中,常常可以给每个结点赋予不同的权值,(一般代表该结点在树中出现的频率)。
带权路径长度,某个结点的带权路径长度一般指的是某个结点到根结点之间的路径长度与该结点的权值乘积的值。这些结点的带权路径长度之和就称为该树的带权路径长度。
2.2哈夫曼树的构造思路
首先,我们要理解哈夫曼树的原理。哈夫曼树是首先寻找n个结点中权值最小的和次小的两个结点,构成一个度为一的小二叉树,接着求出小二叉树对应权值(对应权值大小为两个叶子结点的权值之和),以这个树的根结点为一个结点,来进行和其他结点的权值比较,再次构建出一颗二叉树,求其权值,接着进行循环构建,直到只剩下一个根结点的时候,就表示哈夫曼树构建完成。
其中,这里有个定理,那就是有n个叶子结点的哈夫曼树,一共会有2n-1个结点。这对后面我们实现哈夫曼树算法的时候,编写代码初始化树的时候会有解释。
如上所示,有4个结点,按照上述过程,最后实现的就是上述结果。
2.3构建哈夫曼树
2.3.1构建哈夫曼树的结点类型
哈夫曼树结点一般需要有data数据,weight权重,lchild左孩子结点,rchild右孩子结点,parent双亲结点。
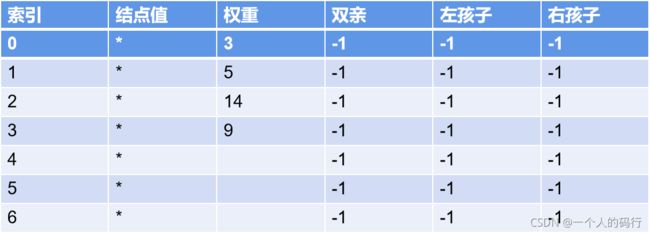
初始状态:有权值的每个结点中有结点值,权重,其他的双亲,左孩子,右孩子等全都默认没有东西,置为-1.
其他的哈夫曼树结点,所有域都为空,双亲,左孩子,右孩子等全都默认没有东西,置为-1。
typedef struct{
char data;
double weight;
int parent;
int lchild;
int rchild;
}HTNode;
上述结点定义好之后,电脑内存中,应该是这样的:
实现算法为
``
void CreateHT(HTNode ht[],int n){
int i,k,lnode,rnode;//定义几个后面要用的变量,lnode和rnode分别存放最小和次小权重的结点位置
double zuixiao ,cixiao;
for(i=0;i<2*n-1;i++)//将每个结点的parent,lchild,rchild等域置为初始值-1
{
ht[i].parent=-1;
ht[i].lchild=-1;
ht[i].rchild=-1;
}
for (i=n;i<=2*n-1;i++)//循环构造哈夫曼树
{
lnode=rnode=-1;
zuixiao=cixiao=999999;//先随便给最小和次小的数字赋一个随意的肯定比所有结点的权重都大
for(k=0;k<=i-1;k++){//循环遍历当前树中有权重的结点
if(ht[k].parent!=-1){//如果该结点没有双亲,则表示不为根结点,可以进行判断
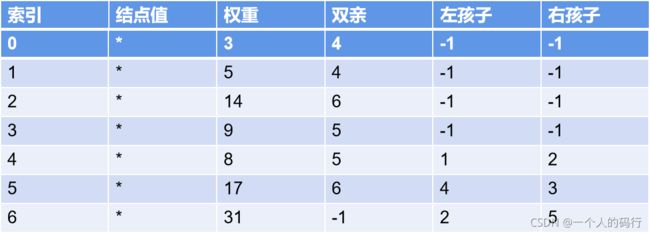
if(ht[k].weight最后算法结束,实现的哈夫曼树的结果如下: