《算法笔记》9.8 哈夫曼树

9.8 哈夫曼树

9.8.1 哈夫曼树

先介绍经典的合并果子问题。

有n堆果子，每堆果子的质量已知，现在需要把这些果子合并成一堆，但是每次只能把两堆果子合并到一起，同时会消耗与两堆果子质量之和等值的体力。显然，在进行n-1次合并之后，就只剩下一堆了。为了尽可能节省体力，请设计出合并的次序方案，使得耗费的体力最少，并给出消耗的体力值。
例如有3堆果子，质量依次为1、2、9，那么可以先将质量为1和2的果堆合并，新堆质量为3，因此耗费体力为3。接着，将新堆与原先的质量为9的果堆合并，又得到新的堆，质量为12，因此耗费体力为12，所以耗费体力之和为3 + 12 = 15，可以证明15为最小的体力耗费值。

为了解决这个问题，不妨进行如下考虑：把每堆果子都看作结点，果堆的质量视作结点的权值，这样合并两个果堆的过程就可以视作给它们生成一个父结点，且父结点的权值等于它们的质量之和，于是把n堆果子合并成一堆的过程可以用一棵树来表示。

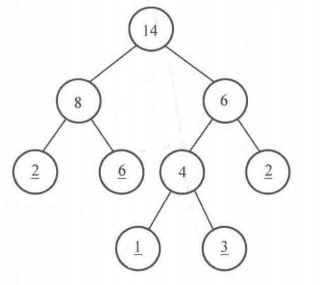
上图是将5堆质量分别为1、2、2、3、6的果子进行合并的某一种方案，可以发现初始的果堆一定处于叶子结点，而非叶子结点都是合并过程中新生成的结点。通过这种方案合并果子所需消耗的体力之和为4+6+8+14=32。

事实上可以发现，消耗体力之和也可以通过把叶子结点的权值乘以它们各自的路径长度再求和来获得，其中叶子结点的路径长度是指从根结点出发到达该结点所经过的边数。例如上面的例子中，从根结点到达权值为6的叶子结点的路径长度为2，而从根结点到达权值为1的叶子结点的路径长度为3，于是32可以通过22+62+13+33+22来计算得到。把叶子结点的权值乘以其路径长度的结果称为这个叶子结点的带权路径长度。例如上面的例子中，权值为6的叶子结点的带权路径长度为62=12，而权值为1的叶子结点的带权路径长度为1*3=3，另外，树的带权路径长度（Weighted Path Length of Tree，WPL）等于它所有叶子结点的带权路径长度之和。

于是合并果子问题就转换成：已知n个数，寻找一棵树，使得树的所有叶子结点的权值恰好为这n个数，并且使得这棵树的带权路径长度最小。带权路径长度最小的树被称为哈夫曼树（又称为最优二叉树）。显然，对同一组叶子结点来说，哈夫曼树可以是不唯一的，但是最小带权路径长度一定是唯一的.

下面将给出一个非常简洁易操作的算法，来构造一棵哈夫曼树：

• 初始状态下共有n个结点（结点的权值分别是给定的n个数），将它们视作n棵只有一个结点的树。
• 合并其中根结点权值最小的两棵树，生成两棵树根结点的父结点，权值为这两个根结点的权值之和，这样树的数量就减少了一个。
• 重复操作回，直到只剩下一棵树为止，这棵树就是哈夫曼树。

例如
初始果堆：

合并后的果堆

通过这个例子也可以发现，对哈夫曼树来说不存在度为1的结点，并且权值越高的结点相对来说越接近根结点。

而在很多实际场景中，不需要真的去构建一棵哈夫曼树，只需要能得到最终的带权路径长度即可（例如合并果子问题就只需要知道消耗的最小体力），因此需要着重掌握的是哈夫曼树的构建思想，也就是反复选择两个最小的元素，合并，直到只剩下一个元素。于是，一般可以使用优先队列
（也可以说堆结构）来执行这种策略。以合并果子问题为例，初始状态下将果堆的质量压入优先队列（注意含义为小顶堆），之后每次从优先队列顶部取出两个最小的数，将它们相加并重新压入优先队列（需要在外部定义一个变量ans，将相加的结果累加起来），重复直到优先队列中只剩下一个数，此时就得到了消耗的最小体力ans，并且方案也可以在这个过程中得到。

#include
using namespace std ;

//小顶堆优先队列
priority_queue< long long , vector<long long> , greater<long long> > q ;

int main(){
    int n ;
    long long temp , x, y, ans = 0 ;
    cin >> n ;
    for( int i = 0 ; i < n ; i++ ){
        cin >> temp ;
        q.push(temp) ;  //将初始果堆压入队列
    }
    
    while( q.size() > 1 ){  //只要优先队列中至少有两个元素
        x = q.front() ;
        q.pop() ;
        y = q.front() ;
        q.pop() ;
        q.push( x + y ) ;       //取出堆顶的两个元素，求和后压入优先队列
        ans += x + y ;      //累计求和结果
    }
    cout << ans ;   //ans即为消耗的最小体力
    return 0 ;
}

9.8.2 哈夫曼编码

对任意一棵二叉树来说，如果把二叉树上的所有分支都进行编号，将所有左分支都标记为0、所有右分支都标记为1，那么对树上的任意一个结点，都可以根据从根结点出发到达它的分支顺序得到一个编号，并且这个编号是所有结点中唯一的。如图

A为00，结点T的编号为10，结点C的编号为100，结点D的编号为101。接着就会发现，对任何一个非叶子结点，其编号一定是某个叶子结点编号的前缀，例如结点T的编号就是结点C和结点D的编号的前缀。并且，对于任何一个叶子结点，其编号一定不会成为其他任何一个结点编号的前缀。

这有什么用呢？假设现在有一个字符串，它由A，B，C，D这四个英文字符的一个或多个组成，例如ABCAD，现在希望把它编码成一个01串，这样方便进行数据传输。能想到的一个办法是把A~D各自用一个01串表示，然后拼接起来即可。例如可以把A用0表示、B用1表示、C用00表示、D用01表示，这样ABCAD就可以用0100001表示。但是很快就会发现，解码的时候无法知道开头的01到底是AB还是D（因为AB和D的编码都是01），因此这种编码方式是不行的。为什么不行呢？这是因为存在一种字符的编码是另一种字符的编码的前缀，例如A的编码是D的编码的前缀，于是一旦有某一种字符的编码拼接在A的编码之后能产生D的编码，就会产生混淆，例如此处把B的编码拼接在A的编码之后能产生D的编码。

因此需要寻找一套编码方式，使得其中任何一个字符的编码都不是另一个字符的编码的前级，同时把满足这种编码方式的编码称为前缀编码。于是很快就会想到，依照本节一开始的说法，只要让这些字符作为一棵二叉树的叶子结点，就能产生需要的编码。因此可以让A用00表示、B用01表示、C用100表示、D用101表示，就可以把ABCAD编码成000110000101，并且不会产生混淆。
再次强调，前缀编码的存在意义在于不产生混淆，让解码能够正常进行。

考虑进一步的问题。对一个给定的字符串来说，肯定有很多种前缀编码的方式，但是为了信息传递的效率，需要尽量选择长度最短的编码方式。假设现在有一个字符串ABACDBAABC，共有十个字符，其中A出现了四次，B出现了三次，C出现了两次，D出现了一次。如果和之前表述的一样，把A用00表示、B用01表示、C用100表示、D用101表示，那么这个字符串编码成01串后的长度将会是4×2+3x2+2x3+1x3=23，我们很快就会发现，如果把A、B，C，D的出现次数（即频数）作为各自叶子结点的权值，那么字符串编码成01串后的长度实际上就是这棵树的带权路径长度，如下图

于是问题就转换成，把每个字符的出现次数作为叶子结点的权值，求一棵树，使得这棵树的带权路径长度最小。事实上这个问题已经解决–就是哈夫曼树。只需要针对叶子结点权值为1、2、3、4建立哈夫曼树，其叶子结点对应的编码方式就是所需要的。这种由哈夫曼树产生的编码方式被称为哈弗曼编码，显然哈弗曼编码是能使给定字符串编码成01串后长度最短的前缀编码。

针对上面的例子，可以构建出图9-68所示的哈夫曼树，其对应的编码方式为：A用0表示、B用10表示、c用110表示、D用111表示，这样ABACDBAABC就可以编码为0100110111001010，长度为19，如图所示。

显然，对一个给定的字符串来说，由于根据频数建立的哈夫曼树可能不唯一，因此对应的哈弗曼编码也可能不唯一，但是将字符串编码成01串的最短长度是唯一的。

最后再次强调，哈弗曼编码是针对确定的字符串来讲的。