强化学习第1天：马尔可夫过程

☁️主页 Nowl

专栏 《强化学习》

君子坐而论道，少年起而行之

​​

一、介绍

什么是马尔可夫过程？马尔可夫过程是马尔可夫决策过程的基础，而马尔可夫决策过程便是大部分强化学习任务的抽象过程，本文将从马尔可夫过程开始，一步步带读者理解马尔可夫决策过程

二、马尔可夫过程

1.状态变化过程

我们知道强化学习是一个状态转移的过程，状态发生变化的原因可能取决于当前状态，也可能取决于先前的许多状态，我们把当前状态设为
$$S_t$$
则下一个状态的概率与之前所有状态有关可表示为
$$P(S_{t+1})=P(S_{t+1}|S_t,...,S_1)$$
下图为某一个状态变化过程图，箭头表示由某个状态变化到另一个状态的概率

2.马尔可夫性质

当且仅当某时刻的状态只取决于上一时刻的状态时，这个过程就具有马尔可夫性质，即
$$P(S_{t+1})=P(S_{t+1}|S_t)$$
可以知道，若某过程满足马尔可夫性质，则我们只需要知道当前状态就可以预测下一个状态，而不是要了解之前所有的状态

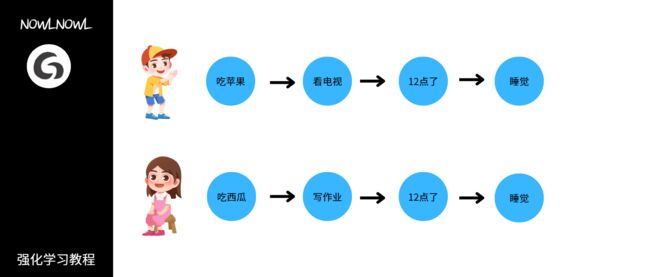
通俗一点可以用下图来说明
无论这两个人之前吃了什么水果，做了什么事，当12点的时候他们都会去睡觉，即睡觉这件事只与12点有关
和之前的行为没有关系

3.马尔可夫过程描述

我们通常用一个元组
$$<S，P>$$
来描述一个马尔可夫过程

• S是有限的状态集合
• P是状态转移矩阵，它记录了状态之间变化的概率

三、马尔可夫奖励过程

1.马尔可夫奖励过程描述

我们知道马尔可夫过程可以由元组来描述，那么马尔可夫奖励过程就可以用元组
$$<S，P，r，\gamma >$$
来描述

• r是奖励函数，r(s)即代表转移到状态s可获得的奖励
• γ是折扣因子，取值范围为[0，1)，我们将在下文感受到折扣因子的作用

2.回报

在一个马尔可夫奖励过程中，从当前状态开始，到终止状态，所有奖励之和为回报
$$G=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+...+{\gamma }^k{R}_{t+k}$$
在这里我们可以看到折扣因子的作用了，折扣因子越接近1，就代表模型更注重长期利益，越接近0，就代表模型更注重短期利益

3.价值函数

在马尔可夫奖励过程中，一个状态的期望回报被称为这个状态的价值，价值函数即是以状态为自变量，价值为因变量的函数，定义如下
$$V(s)=E[G_t|S_t=s]$$
它表示了所有状态回报之和的一种平均，可能这里有些人对这个期望不是很理解，既然我的S固定了，那G不也就固定了吗，为什么还要加上一个期望呢，想到这点的说明有自己的思考了，S确实固定了，这时我们去看G，G这时真的是固定值吗？

理解了价值函数之后，我们接着往下看

4.贝尔曼方程

首先我们给出贝尔曼方程的定义
$$V(s)=r(s)+\gamma \sum _{s^{{}^{\prime }}}P(s^{{}^{\prime }}|s)V(s^{{}^{\prime }})$$
可以看到左边就是一个价值函数，那是怎么推导过来的呢，看以下过程，我们将价值函数拆开
$$V(s)=E[G_t|S_t=s]$$
$$=E[R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+...|S_t=s]$$
$$=E[R_t+\gamma (R_{t+1}+\gamma R_{t+2}+...)|S_t=s]$$
$$=E[R_t+\gamma G_{t+1}|S_t=s]$$
$$=E[R_t+\gamma V(S_{t+1})|S_t=s]$$
其中
$$r(s)=E[R_t|S_t=s]$$
而根据条件期望的定义可以得到
$$\gamma \sum _{s^{{}^{\prime }}}P(s^{{}^{\prime }}|s)V(s^{{}^{\prime }})=E[\gamma V(S_{t+1})|S_t=s]$$
即证贝尔曼方程
$$V(s)=r(s)+\gamma \sum _{s^{{}^{\prime }}}P(s^{{}^{\prime }}|s)V(s^{{}^{\prime }})$$

四、马尔可夫决策过程

1.马尔可夫决策过程描述

我们已经知道了马尔可夫过程和马尔可夫奖励过程（MDP）的描述，接下来我们描述马尔可夫决策过程（MAP），使用元组描述
$$<S，A，P，r，\gamma >$$

• A是动作，这时多出来的东西可不只有动作，还有抉择做什么动作的策略
• 此时r(s)变为了r(s，a)，因为奖励此时不仅与状态有关，还与动作有关
• 同理，P也与动作联系起来了，因此它不再是一个二维数组矩阵，而是变成了一个三维矩阵

在描述马尔可夫决策过程的元组中，我们发现了许多强化学习中的元素：状态，奖励，动作，可以看到我们逐渐与我们的目的——强化学习越来越近了！

由于新加入的动作因子所产生的策略因子，我们优化一下价值函数变为状态价值函数
$$V^{\pi }(s)=E_{\pi }[G_t|S_t=s]$$
我们把π定义为策略，则更新后的价值函数可以这样描述：从状态s出发遵循策略π可以获得的期望回报

定义好了状态价值函数，我们再来定义动作价值函数，动作价值函数是遵循策略π时，在当前状态下采取动作a能得到的期望回报
$$Q^{\pi }(s，a)=E_{\pi }[G_t|S_t=s，A_t=a]$$
我们直观理解一下

发现了其中的区别了吗，状态价值函数的第一个状态是固定的，而动作价值函数的第一，第二个状态都是固定的，回到定义，因为动作价值函数规定了当前状态所做出的动作，所以第二个状态也是固定的

所以状态价值函数与动作价值函数的联系公式如下
$$V^{\pi }(s)=\sum _a\pi (a|s)Q^{\pi }(s，a)$$

展开动作价值函数的贝尔曼方程如下
$$Q^{\pi }(s，a)=r(s，a)+\gamma \sum _{s^{{}^{\prime }}}P(s^{{}^{\prime }}|s，a)V^{\pi }(s^{{}^{\prime }})$$

2.贝尔曼期望方程

动作价值函数贝尔曼期望方程
$$Q^{\pi }(s，a)=E_{\pi }[R_t+\gamma Q^{\pi }(s^{{}^{\prime }}，a^{{}^{\prime }})|S_t=s，A_t=a]$$
$$=r(s，a)+\gamma \sum _{s^{{}^{\prime }}}P(s^{{}^{\prime }}|s，a)\sum _{a^{{}^{\prime }}}\pi (a^{{}^{\prime }}|s)Q^{\pi }(s^{{}^{\prime }}，a^{{}^{\prime }})$$
状态价值函数贝尔曼期望方程
$$V^{\pi }(s)=E_{\pi }[R_t+\gamma V^{\pi }(s^{{}^{\prime }})|S_t=s]$$
$$=\sum _a\pi (a|s)\{r(s，a)+\gamma \sum _{s^{{}^{\prime }}}P(s^{{}^{\prime }}|s，a)V^{\pi }(s^{{}^{\prime }})\}$$
贝尔曼方程是强化学习中很重要的部分，之后很多方法都是由此推导而来，请一定好好理解并尝试推导

五、蒙特卡洛方法

1.介绍

蒙特卡洛方法的思想来自于概率论与数理统计，主要步骤是先进行重复随机抽样，然后运用概率统计方法来获得我们想要的数值特征

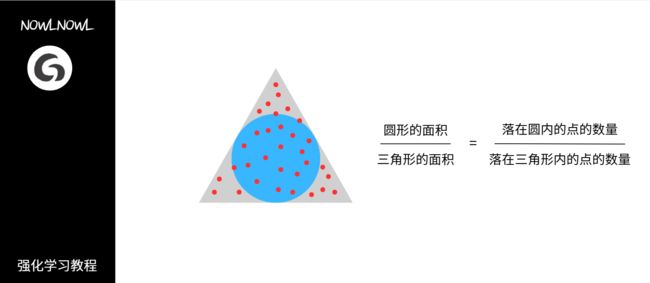
如下是一个简单的例子，使用蒙特卡洛方法求圆的面积，我们已知三角形的面积，则先随机选取多个点，然后就可以通过比例计算出圆形的面积

2.在强化学习中的应用

那么如何在强化学习中应用蒙特卡洛方法呢，我们试着求状态价值，我们知道状态价值是状态的期望回报，这个回报由许多条序列计算而来，那我们就可以选取多条序列，将通过选取的序列所算出来的期望回报近似为真正的状态价值
$$V^{\pi }(s)=E_{\pi }[G_t|S_t=s]\approx \frac{1}{N}\sum _i^N{G}_t^{(i)}$$

根据大数定律可以知道，当选取的序列够多时，这两个值就越近似

3.为什么要使用蒙特卡洛方法

我们要明白，虽然我们知道了求解期望的公式，但在真实情况中，很多条件是不知道的，例如不清楚某个状态的所有序列，这时我们就只能使用蒙特卡洛方法来通过局部估计总体了

最优策略

作了这么多基础铺垫，再回到强化学习上来吧，强化学习的目标就是找到一个策略，来获得最高的期望回报，从初始状态出发到达最终目的可能有很多策略，但很容易知道，一定有一个策略，得到的期望不低于其他所有策略，这个策略就是最优策略，找到它就是强化学习的目标

我们将最优策略表示为
$${\pi }^{\ast }(s)$$
再定义最优状态价值函数
$$V^{\ast }(s)=ma{x}_{\pi }{V}^{\pi }(s)$$
和最优动作价值函数
$$Q^{\ast }(s，a)=ma{x}_{\pi }{Q}^{\pi }(s，a)$$

贝尔曼最优方程

前文介绍了最重要的贝尔曼方程，这里给出它的最优形式
$$Q^{\ast }(s，a)=r(s，a)+\gamma \sum _{s^{{}^{\prime }}}P(s^{{}^{\prime }}|s，a)ma{x}_{a^{{}^{\prime }}}{Q}^{\ast }(s^{{}^{\prime }}，a^{{}^{\prime }})$$
$$V^{\ast }(s)=ma{x}_a(r(s，a)+\gamma \sum _{s^{{}^{\prime }}}P(s^{{}^{\prime }}|s，a)V^{\ast }(s^{{}^{\prime }}))$$

感谢阅读，觉得有用的话就订阅下《强化学习》专栏吧，有错误也欢迎指出