数学建模——经典美赛O奖论文65123研读

一、原题目概述

这是美赛2017E题优秀论文。题目要求利用smart growth theories（智能成长理论）及相关原则，评价城市及发展计划并利用该理论规划不同情况下城市的发展计划。具体要求如下（翻译版）：

1.定义衡量城市智能增长成功率的指标。这应该考虑可持续性的三个E和/或智能增长的十项原则。
2.研究选定城市的当前增长计划。衡量和讨论每个城市当前的增长计划如何满足智能增长原则。怎么根据你的标准，目前的计划是成功的吗？
3.使用智能增长原则在未来几十年内为两个城市制定增长计划。写出支持您基于您城市的地理，预期增长率和经济机会的计划以及选择您的组件和主动性的原因。用你的度量来评估你的智能增长计划的成功。
4.也使用您的指标，将您重新设计的智能增长计划中的各项计划排名为最具潜力的潜力最小。比较和对比这些倡议及其在两个城市之间的排名。
5.假设每个城市的人口在2050年将增加50％，解释你的计划以什么方式支持这个水平的增长？

您的ICM提交应包含1页的摘要表，您的解决方案不能超过20页，最多21页。注意：附录和参考文献不计入20页的限制。

二、论文处理

在看一篇优秀论文时，学习论文的解题思路是重中之重，**其次是论文的细节，包括模型写作、可视化、安排布局等等。**美赛是一个相对开放的比赛，在给定情境下可以有很多解题方式。但是想要拿到不错的奖项，就要尽量向评委期待的思路靠拢。优秀论文的解题方式，代表了评委认可的思路。

下面，我们来看这篇文章的作者是怎么解决如上问题的：

指标选择（内含数据预处理）：文章笔者查找了两个城市权威数据与资料，使用聚类算法得出指标相似性，由此得到用于建立标准的 $10$ 个城市的数据，并采取了相关丢失数据填写的策略（使用插值算法）；
采用主成分分析法将 $88$ 个指标基于 3E 原则和上述的十个原则缩减至 $25$ 个；
对 $25$ 个指标作正向化、标准化处理；
使用模糊评价的方法量化指标，进行打分；
利用熵权法与优化模型/群体决策法得到指标权重；
建立了 $5$ 个二级指标并在指标体系和权重法的基础上，提出了一种衡量城市智能增长成功程度（SDSG）成功程度的综合指标。采用指标系统提供基本的二级指标，采用权重法评价 SGSD 的权重；
最终建立三级评价体系及利用 K-means 算法建立一个合适的标准来评估城市智能增长的成功程度

三、论文写作

1. Title

本文标题“城市设计中的智能增长理论”直切主题，紧扣与题目关系，与国赛标题要求基本一致；

2. Summary

概括内容

解决问题+应用方法+得到结果

开头+针对问题一、二、三+结尾

（1）开头：

1. 背景

2. 交代做的事

3. 实际意义

（2）中间段：

1. 解决了什么问题

2. 紧扣题目说明应用方法

3. 得到结果

（3）结尾：总结全文，介绍亮点，推广

总的来说与国赛摘要写法基本一致

1. Contents

目录要写明各部分标题及其下设小标题，并表明所对应页码，最后单独列出参考文献和附录。

2. Introduction

本文介绍部分设立“背景”与“问题陈述与分析”两个小标题，其中背景可以参考文献，问题的陈述与分析部分主要是梳理完成题目所给任务要做的事务，使用“首先”“然后”“最后”等字眼使逻辑清晰，并附上严谨的流程图解。

3. Assumption and Symbol Explanation

本文假设与符号说明部分其实相当于国赛论文模板中第三第四部分综合，该部分理所当然分为“假设”与“符号说明”两部分，本文假设主要是排除了小概率事件及次要因素，符号说明部分制作对照表赋予英文大写缩写以解释。

4. Task

4.1数据的选取

​ 通过阅读此论文，我了解了数据选取的几个基础：

• 1.数据量足够
• 2.保证数据的可用性、连续性、真实性
• 3、可使用聚类的方法对数据分组、检索

4.2数据的处理

​ 此论文主要是对缺失数据进行填充，介绍了如下方法：

• 1、如果指标值平滑，则可以采用之前的数据进行替换
• 2、如果能得到前后的数据，可以取平均值作为缺失。
• 3、如果两组相似，则可以用另一组中相同位置的值替换其中一组中缺失的数据。

4、数据拟合采用插值法

4.3指标的选择

​ 论文首先选择了88个指标当很明显指标过多，所以论文采取了基于3E原则和10原则的主成分分析来进行减少指标最后将指标减少到25个

4.4数据归一化

​ 论文将25个指标分为成本型、效益型和适度型三种类型。在三类指标中，成本型指标越小，智能成长的成功程度越好，效益类型指数则相反。中等类型的指数越接近某一特定值越好。由于指标的贡献不同，三类数据采用不同的归一化方式如下。

成本型

$$x_{ij}=\frac{x_j^{max}-x_{ij}}{x_j^{max}-x_j^{min}},i=1,\cdots ,25;j=1,2$$

效益型

$$x_{ij}=\frac{x_{ij}-x_j^{min}}{x_j^{max}-x_j^{min}},i=1,2,\cdots 23;j=1,2$$

中等类型

$$x_{ij}=\{\begin{array}{l}1-\frac{s_1-d_{ij}}{max\{s_1-d_j^{min},d_j^{max}-s_2\}}{d}_{ij}<s_1\\ 1d_{ij}=s_1\\ 1-\frac{d_{ij}-s_2}{max\{s_1-d_j^{min},d_j^{min}-s_2\}}{d}_{ij}>s_1\end{array}$$

需要注意的是本论文对成本型的归一化与清风的方法不同且看起来比较高级可以学习

4.5定性指标的量化

​ 论文采取了模糊评价法来将定性指标转化为定量指标，因为我还没学故不多加分析

接下来的部分本文一个任务用了一大节来写，其中以第一个任务尤为重要，分别以“数据预处理”“主指示器系统”“评价指标的加权模型”“综合评价指标”“智能增长的指标”五个部分组成，具体做法后面再总结。

5. Sensitivity Analysis

即国赛模型检验中灵敏度分析，控制变量观察指标变化幅度。

6. Strengths and Weaknesses

描述模型的优势与劣势。

7. References

参考文献

8. Appendix

附录

三. 数学模型方法部分

Ⅰ. K-Means聚类分析

聚类原本是统计学上的概念，现在属于机器学习中非监督学习的范畴，大多都被应用在数据挖掘、数据分析的领域，简单说可以用一个词概括——物以类聚。从定义上讲，聚类就是针对大量数据或者样品，根据数据本身的特性研究分类方法，并遵循这个分类方法对数据进行合理的分类，最终将相似数据分为一组，也就是**“同类相同、异类相异”**。

K-Means 聚类法的原理和过程：

1. 确定分组数

K-Means 聚类法中的 $K$ 就是分组数，也就是我们希望通过聚类后得到多少个组类。比如我有下面八个数据，想要将这些数据分成两类，那么 $K=2$ 。

图片来自知乎

2. 随机选择 $K$ 个值作为数据中心

这个数据中心的选择是完全随机的，也就是说怎么选择都无所谓，因为这里 $K=2$ ，所以我们就以 $A$ 和 $B$ 两个为数据中心。

3. 计算其他数值与数据中心的“距离”

这里我们要引入欧氏距离的概念，通俗点说欧氏距离就是多维空间中各个点之间的绝对距离，表明两点之间的距离远近，其公式为：

$$
\begin{aligned}

\text{dist}(X,Y) = \sqrt{\sum\limits_{i = 1} ^ {n} (x_i - y_i)^{2}}

\end{aligned}
$$
如果是普通的二维数据，这个公式就直接变成了勾股定理，因此我们算出其他 $6$ 个点距离 $A$ 和 $B$ 的距离，谁离得更近，谁与数据中心就是同一类。

图片来自知乎

所以，我们可以看出，$C,D,\cdots ,H$ 距离 $B$ 的距离都比距离 $A$ 更近，所以第一次分组为：

• 第一组：$A$

• 第二组：$B,C,D,E,F,G,H$

4. 重新选择新的数据中心

得到了第一次分组的结果，我们再重复前两个步骤，重新选择每一组数据的数据中心。

• 第一组只有 $A$，所以 $A$ 仍然是数据中心；

• 第二组有 $7$ 个数值，将这个 $7$ 个数值的平均值作为新的数据中心，我们将其命名为 $P$，计算平均坐标为 $(5.14,5.14)$ 。

5. 再次计算其他数据与新数据中心的距离

还是直接计算勾股定理，计算出其他数据与 $A$ 和 $P$ 的欧氏距离，如下：

图片来自知乎

我们可以看出这里面有的距离 $A$ 近，有的距离 $P$ 近，于是第二次分组为：

• 第一组：$A,B$

• 第二组：$C,D,E,F,G,H$

6. 再次重新选择数据中心

这里就是老规矩了，继续重复前面的操作，将每一组数据的平均值作为数据中心：

• 第一组有两个值，平均坐标为 $(0.5,1)$ ，这是第一个新的数据中心，命名为 $O$ 。

• 第二组有六个值，平均值为 $(5.8,5.6)$ ，这是第二个新的数据中心，命名为 $Q$ 。

7. 再次计算其他数据与新数据中心的距离

图片来自知乎

这时候我们发现，只有 $A$ 与 $B$ 距离 $O$ 的距离更近，其他 $6$ 个数据都距离 $Q$ 更近，因此第三次分组为：

• 第一组：$A,B$

• 第二组：$C,D,E,F,G,H$

经过这次计算我们发现分组情况并没有变化，这就说明我们的计算收敛已经结束了，不需要继续进行分组了，最终数据成功按照相似性分成了两组。

8. 方法总结

简单来说，我们一次次重复这样的选择数据中心-计算距离-分组-再次选择数据中心的流程，直到我们分组之后所有的数据都不会再变化了，也就得到了最终的聚合结果。

Ⅱ. 主成分分析

PCA(Principal Component Analysis) 是一种常见的数据分析方式，常用于高维数据的降维，可用于提取数据的主要特征分量。PCA通常用于降低大型数据集的维数，方法是数据集中的指标数量变少，并且保留原数据集中指标的大部分信息。总而言之：减少数据指标数量，保留尽可能多的信息。

PCA方法步骤：

1. 标准化连续初始变量的范围（非结构化转成结构化）

此步骤的目的是标准化结构化指标的范围，因为 PCA 对于初始变量的方差非常敏感，如果初始变量的范围之间存在较大差异，则会造成很大变差，使用标准化可以将数据转换为可比较的尺度。最常用的方法主要有一下两种：

1. 线性函数归一化：将原始数据进行线性变换，使结果映射到 $[0,1]$ 的范围，实现对原始数据的等比缩放。归一化公式如下：
   $$
   \begin{aligned}

   X_{\text{norm}} = \frac{X - X_{\min}}{X_{\max} - X_{\min}}

   \end{aligned}
   $$

2. 零均值归一化：它会将原始数据映射到均值为 $0$ ，标准差为 $1$ 的分布上。具体来说，假设原始特征的均值 $\mu$ ，标准差为 $\sigma$ ，那么归一化公式定义为：
   $$\begin{array}{r}z=\frac{x-\mu }{\sigma }\end{array}$$

2. 计算协方差矩阵以识别相关性

此步骤的目的是观察数据标签彼此是否存在相关性，观察指标间是否包含冗余信息。使用协方差矩阵是一个 $p\times p$ 对称矩阵（其中 $p$ 是维数），它具有与所有可能的初始变量对相关联的协方差作为条目。假设三个变量 $x,y,z$ 三维数据集，协方差矩阵是 $3\times 3$ 矩阵如下：
[ Cov ( x , y )     Cov ( x , y )     Cov ( x , z ) Cov ( y , x )     Cov ( y , y )     Cov ( y , z ) Cov ( z , x )     Cov ( z , y )     Cov ( z , z ) ] \left[\begin{matrix} \text{Cov}(x,y) \ \ \ \ \text{Cov}(x,y) \ \ \ \ \text{Cov}(x,z) \\ \text{Cov}(y,x) \ \ \ \ \text{Cov}(y,y) \ \ \ \ \text{Cov}(y,z) \\ \text{Cov}(z,x) \ \ \ \ \text{Cov}(z,y) \ \ \ \ \text{Cov}(z,z) \\ \end{matrix} \right] ​Cov(x,y)    Cov(x,y)    Cov(x,z)Cov(y,x)    Cov(y,y)    Cov(y,z)Cov(z,x)    Cov(z,y)    Cov(z,z)​ ​
自身协方差是自身的方差，即 $\text{Cov}(a,b)=\text{Cov}(b,a)$ ，意味着上三角部分和下三角部分相等。如果协方差为正，则两个变量正相关，如果协方差为负，则两个变量呈负相关。

3. 计算协方差矩阵的特征向量和特征值以识别主成分

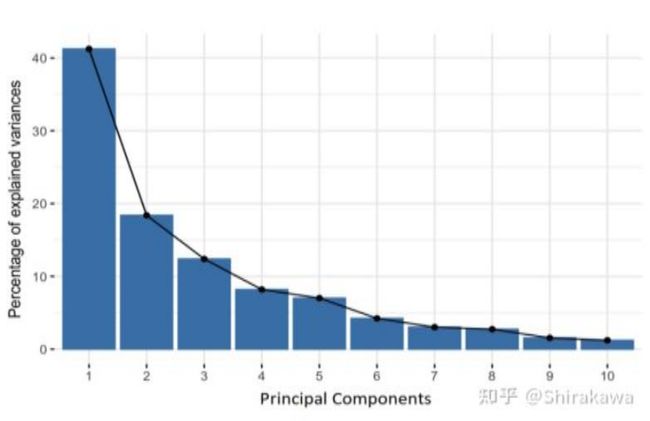
通过计算协方差矩阵的特征向量和特征值来确定数据的主成分。首先解释一下主成分定义：主成分是由初始变量的线性组合或混合构成的新变量。新变量是互不相关的，并且初始变量中的大部分信息被挤压或压缩到第一成分中。通俗来讲，十维数据给十个主成分，PCA 试图将最大可能信息放在第一个组件中，然后第二组件中放置最大的剩余信息，以此类推，直到出现如图所示内容：

图片来自知乎

通过这种方式在主成分中组织信息，可以在不丢失太多信息的情况下降低维数生成新的指标。此时的新指标互不相关且无可解释性。它们是初始变量的线性组合。主成分表示解释最大方差量的数据的方向。方差与信息的关系是，一条携带的方差越大，沿线的数据点的离散度越高，沿线的离散度越大，它所包含的信息越多。计算协方差矩阵的特征值其实就是计算最大的方差，计算其对应的特征向量就是最佳投影方向，计算协方差矩阵特征值需要将其对角化，为了满足变化后的指标间协方差为 $0$ 且指标方差尽可能大，因此要求解最大化问题，可表示为：
$$
\left{

\begin{matrix}
\max{\omega^{T}\Sigma\omega } \
\text{s.t.}\ \ \ \ \omega^{T}\omega = 1
\end{matrix}

\right.
KaTeX parse error: Can't use function '$' in math mode at position 43: …ω求导令其等于0，便可以推出 $̲\Sigma\omega = …
\begin{aligned}
D(x) = \omega^{T}\Sigma\omega = \lambda\omega^{T}\omega = \lambda
\end{aligned}
$$
将计算好的特征值的顺序对特征向量进行排序，从高到低，可以按照重要程度顺序获得主成分。

4. 创建特征向量来决定保留哪些主成分

计算特征向量并按照特征值降序对他们进行排序，使我们可以按照重要性顺序找到主成分。在这一步骤我们选择保留所有特征值还是丢弃那些重要程度较低的特征值。并与剩余的特征值形成一个成为特征向量的向量矩阵。特征向量只是一个矩阵，列为我们决定保留的特征向量。此步骤根据我们的需求来决定。通常是取特征值前 $d$ 对应的特征向量量 ${\omega }_1,{\omega }_2,\cdots ,{\omega }_d$ ，通过以下映射将 $n$ 维样本映射到 $d$ 维；
$$
x_i’ = \left[

\begin{matrix}

\omega_{1}^{T} x_i \
\omega_{2}^{T} x_i \
\vdots \
\omega_{d}^{T} x_i \

\end{matrix}

\right]
KaTeX parse error: Can't use function '$' in math mode at position 5: 新的 $̲x_i'$ 的第 $d$ 维就…
\eta = \sqrt{\frac{\sum_{i = 1}^{{d}\lambda_{i}}{2}}{\sum_{i = 1}^{{n}\lambda_{i}}{2}}}
$$
5. 沿主成分轴重铸数据

在这一步骤，使用协方差矩阵的特征向量形成的特征值，将数据从原始轴重新定向到主成分表示的轴。可以将原始数据集的转置乘以特征向量的转置来完成。

6. 总结

除了使用目标函数求解最大方差外，可以考虑其他思路分析，例如最小回归误差得到新的目标函数。实际上对应原理和求解方法与该方法是等价的。PCA 是一种线性降维方法，具有一定的局限性，可以考虑通过核映射对 PCA 机械能扩展得到核主成分分析（KPCA），可以通过流形映射降维方法，比如等距映射，局部线性嵌入，拉普拉斯特征映射等，对一些 PCA 效果不好的复杂数据集进行非线性降维操作。

Ⅲ. 模糊评价

1. 建立综合评价的因素集

因素集是以影响评价对象的各种因素为元素所组成的一个普通集合，通常用 $U$ 表示，$U=(u_1,u_2,\cdots ,u_m)$ ，其中元素 $u_i$ 代表影响评价对象的第 $i$ 个因素。这些因素通常都具有不同程度的模糊性。

例子：

这里设评定科研成果等级的指标集为 $U=(u_1,u_2,u_3,u_4,u_5)$ ，$u_1$ 表示为科研成果发明或创造、革新的程度，$u_2$ 表示安全性能，$u_3$ 表示经济效益，$u_4$ 表示推广前景，$u_5$ 表示成熟性。

2. 建立综合评价的评价集

评价集是评价者对评价对象可能做出的各种结果所组成的集合，通常用 $V$ 表示，$V=(v_1,v_2,\cdots ,v_m)$ ，其中元素 $v_j$ 代表第 $j$ 种评价结果，可以根据实际情况的需要，用不同的等级、评语或数字来表示（注意下文中出现的 $m$ 和 $n$ ，$m$ 表示 $m$ 个因素集，$n$ 表示 $n$ 个评价集）。

这里设评定科研成果等级的评价集为 $V=(v_1,v_2,v_3,v_4)$ ，其中 $v_1,v_2,v_3,v_4$ 分别表示很好、较好、一般、不好（或者一等奖、二等奖、三等奖、四等奖，或者金牌、银牌、铜牌、铁牌）。

3. 进行单因素模糊评价，获得评价矩阵

若因素集 $U$ 中第 $i$ 个元素对评价集 $V$ 中第 $1$ 个元素的隶属度为 $r_{i_1}$ ，则对第 $i$ 个元素单因素评价的结果用模糊集合表示为：$R_i=(r_{i_1},r_{i_2},\cdots ,r_{i_n})$ ，以 $m$ 个单因素评价集 $R_1,R_2,\cdots ,R_m$ 为行组成矩阵 $R_{m\times n}$ ，称为模糊综合评价矩阵。

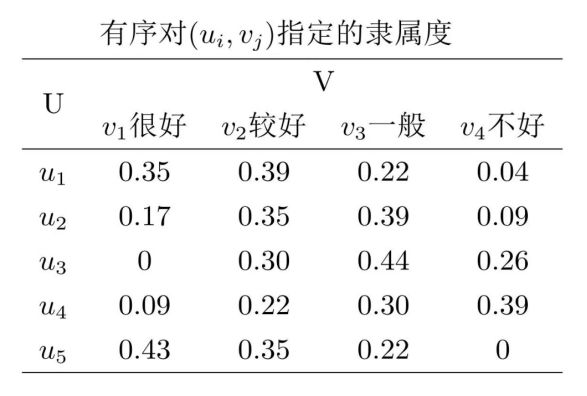
在实例中，某项科研成果通过专家评审打分，按下表给出 $U\times V$ 上每个上每个有序对 $(u_i,v_i)$ 指定的隶属度：

得到单因素评判矩阵 $R$ ：
$$
R = \left[\begin{matrix}
0.35 &0.39 &0.22 &0.04 \
0.17 &0.35 &0.39 &0.09 \
0 &0.30 &0.44 &0.26 \
0.09 &0.22 &0.30 &0.39 \
0.43 &0.35 &0.22 &0

\end{matrix}
\right]
$$
4. 确定因素权向量

评价工作中，各因素的重要程度有所不同，为此，给各因素 $u_i$ 一个权重 $a_i$ ，各因素的权重集合的模糊集，用 $A$ 表示：$A=(a_1,a_2,\cdots ,a_m)$ 。

在实例中，为了评定作者的学术成就，取权数分配 $A=(0.35,0.35,0.1,0.1,0.1)$ 。（这里给出的权向量较为简便，其实可以通过层次分析法 AHP 的成对比较阵来构造这个权向量。）

5. 建立综合评价模型

确定单因素评判矩阵 $R$ 和因素权向量 $A$ 之后，通过模糊变化将 $U$ 上的模糊向量 $A$ 变为 $V$ 上的模糊向量 $B$ ，即 $B=A_{1\times m}\circ R_{m\times n}=(b_1,b_2,\cdots ,b_n)$ 。 其中 $\circ$ 称为综合评价合成算子，这里取成一般的矩阵乘法即可。

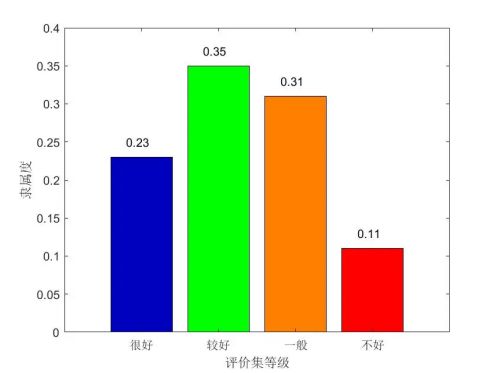
在实例中，最后得到的模糊向量为 $B=A\times R=(0.23,0.35,0.31,0.11)$ ，由计算结果可见（如下图），该成果应被评为二等奖。

6. 确定系统总得分

综合评价模型确定后，确定系统得分，即 $F=B_{1\times n}\times S_{1\times n}^T$ ，其中 $F$ 为系统总得分，$S$ 为 $V$ 中相应因素的级分。
在实例中，一等奖的级分肯定最高，其次是二等奖，依次往下，设级分依次为 $S=(100,80,60,30)$ ，则该成果最后的系统总得分为 $72.9$ 。

如果是多目标的模糊综合评价，对于同一批专家打分，最后的系统总得分就相对来说较为可信，从本例来看，就可以对各个成果相互比较最后的综合得分。

Ⅳ. 熵权法

**信息量：**信息量是度量弄清楚一个未知事物需要查询的信息的多少，单位是比特。随机变量取某个值时，其概率倒数的对数就是信息量。通俗的说就是，事物所含信息量与其发生的概率负相关。一件事物出现的概率决定了它的不确定性大小，也就决定了所含信息量的大小。出现的概率越大，不确定性越小，所含信息量也就越小。
$$
\begin{aligned}

I_i = \log_{2}\left(\frac{1}{p_i}\right) = -\log_{2} p_{i}

\end{aligned}
$$\ast \ast 信息熵：\ast \ast 信息熵也就是信息量的期望。可以把信息熵理解成不确定性的大小，不确定性越大，信息熵也就越大。$$
H(X) = \sum\limits_{i = 1}^{n} p_{i} \times \log_2\left(\frac{1}{p_i}\right)
$$
$X$ 表示的是一个信源。信息量是对信源发出的某一个信号所含信息的度量，信息熵是对一个信源所含信息的度量，也就是信息量的期望。熵权法的基本思路是根据指标变异性的大小来确定客观权重。

一般来说，若某个指标的信息熵越小，表明指标值得变异程度越大，提供的信息量越多，在综合评价中所能起到的作用也越大，其权重也就越大。相反，某个指标的信息熵越大，表明指标值得变异程度越小，提供的信息量也越少，在综合评价中所起到的作用也越小，其权重也就越小。以下为步骤：

1. 数据标准化

首先将各个指标进行去量纲化处理，假设给定了 $m$ 个指标 $X_1,X_2,\cdots ,X_m$ ，其中 $X_i=\{x_1,x_2,\cdots ,x_n\}$ 。假设对各指标数据标准化后的值为 $Y_1,Y_2,\cdots ,Y_m$ ，那么
$$
\begin{aligned}

Y_{ij} = \frac{X_{ij} - \min(X_i)}{\max(X_i) - \min(X_i)} (正向指标时) \

\end{aligned}
$$或$$
\begin{aligned}

Y_{ij} = \frac{\max(X_i) - X_{ij}}{\max(X_i) - \min(X_i)} (逆向指标时) \

\end{aligned}
$$
2. 求各指标在各方案下的比值

也就是第 $j$ 项指标在第 $i$ 个方案中占该指标的比重，其实也就是为了计算该指标的变异大小。
$$p_{ij}=\frac{Y_{ij}}{\sum _{i=1}^n{Y}_{ij}},i=1,2,\dots ,n,j=1,2,\dots ,m$$
3. 求各指标的信息熵

根据信息论中信息熵的定义，一组数据的信息熵为：
$$E_j=-\ln (n{)}^{-1}\sum _{i=1}^n{p}_{ij}\ln p_{ij}$$
其中 $E_j\ge 0$ 。若 $p_{ij}=0$ ，定义 $E_j=0$ 。

4. 确定各指标的权重

根据信息熵的计算公式，计算出各个指标的信息熵为 $E_1,E_2,\cdots ,E_m$ 。

• 4.1 通过信息熵计算各指标的权重：
  $$
  \begin{aligned}

  w_j = \frac{1 - E_j}{k - \Sigma E_j} (j = 1, 2, \dots, m)

  \end{aligned}
  $$
  这里 $k$ 指的是指标个数，即 $k=m$ 。

• 4.2 通过计算信息冗余度来计算权重：

  令 $D_j=1-E_j$ ，然后计算权值：
  $$w_j=\frac{D_j}{\sum _{j=1}^m{D}_j}$$

5. 最后计算每个方案的综合评分
$$\begin{array}{r}{s}_i=\sum _{j=1}^m{w}_j\times X_{ij}\end{array}$$